代价树的盲目搜索原理及应用

在前面的宽度优先搜索和深度优先搜索中，提到的最优解指的是找到的解是距离初始状态节点最近的解，其实这里有个假定条件，就是认为扩展出的子节点距离都是相等的，也就是代价（cost）都是相同的，可以假定都为1，但是在有些实际问题中，例如地图搜索，找起点到终点的最短路径，就不能仅仅是看路径经过了多少中间节点，即是否深度最小，还必须考虑各节点之间的距离。对图3.2进行修改，添加上各节点之间的距离，如图3.8所示，在从一个节点到下一个节点进行扩展的时候，必须同时还要考虑距离。这类问题还被称为旅行商问题（TSP，traveling salesman problem），是数学领域中著名问题之一。它假设有一个旅行商人要拜访N个城市，每个城市只能拜访一次，而且最后还要回到原来出发的城市，他怎样才能选择出最短的路径？

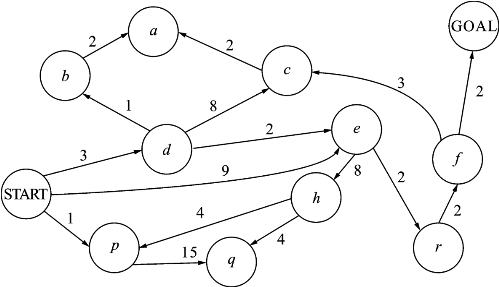
图3.8　包含节点间距离的状态空间图

不考虑距离，从START到d、e、p的代价是一样的；考虑距离后，从START到d、e、p的距离分别是3、9、1，也就是说从START到d、e、p的代价是不一样的，此时搜索的策略就需要调整了，需要考虑到代价。同样，考虑到代价的搜索可以分为代价树的宽度优先搜索和代价树的深度优先搜索两种类型。实际上，代价树的盲目搜索过程与之前讨论过的宽度优先搜索和深度优先搜索也是相似的，只是在待扩展的节点的选取上有所不同，需要考虑到代价。具体来说，就是在放入OPEN表中时，还需要计算代价参数，OPEN表中的节点始终按照代价大小排序，选择代价最小的节点移入CLOSED表中进行扩展，而且如果扩展的节点已经在OPEN表中，但是其代价值比OPEN表中的代价值更低，则需要替换掉OPEN表中的节点并重新排序。

首先看一下代价树的宽度优先搜索。该算法更多地被称为等代价搜索或一致性代价搜索（UCS，uniform cost search），它每次扩展节点时，需要计算所有后继状态节点的代价，并与OPEN表中所有的节点进行排序，选择排在最前面、代价最小的节点进行扩展。它同宽度优先搜索一样，是一个完备的、具有最优性的算法，只是它的完备性有个前提条件，就是每一步的代价都大于或等于某个正常数，即不存在零代价，否则可能会陷入死循环。

数据结构课程中的单源最短路径算法用来求一个图中一个顶点到其他各个顶点的最短路径，也称为狄杰斯特拉算法（Edsger W.Dijkstra，1965），思路就和代价树的宽度优先搜索类似。

代价树的宽度优先搜索的缺点是可能在每个方向上进行扩展，没有任何包含目标位置的信息，依然属于盲目搜索。比如，搜索从武汉到北京经过各省会城市最短的路径，采用代价树的宽度优先搜索会先从武汉搜索到南昌节点，而不是优先考虑朝向北京方向的郑州，因为在与武汉相邻的省会城市中，南昌距离武汉最近，如果这样去搜索，就谈不上智能了，效率较低。

在代价树的深度优先搜索中，每次扩展节点时，也需要计算所有后继状态节点的代价，但是只从后继状态节点中选择代价最小的节点进行扩展。它和深度优先搜索一样，不是一个完备的算法，获得的解可能不是最优解，甚至有可能进入无穷分支而得不到解。因此，常用有限代价深度优先搜索来解决实际问题。

下面，针对图3.8所示的搜索问题，采用代价树的宽度优先搜索，用Python来实现。

1.图的存储方案考虑

参考数据结构中图的存储方法，采用类似邻接表的方式，并且为了使代码能更通用并且考虑到Python的字符处理方式比较灵活，用maps.txt文档来存储待搜索的状态空间图，每一行存储一个节点及其可以到达的相邻节点和代价（距离），用空格分开，具体如下：(www.xing528.com)

然后在程序中，读入该文本文件的每一行并进行拆分，用字典graph来保存该图。实现这部分功能的代码定义在main（）函数中。

2.代码实现的基本思路

为了简化，使用Python的队列模块（queue）。该模块提供了同步的、线程安全的队列类，包括FIFO队列Queue、LIFO堆栈Lifo Queue和优先级队列Priority Queue。其中，优先级队列Priority Queue在普通先入先出队列的基础上增加了优先级参数，进入该队列的元素还需要按照优先级进行排序，优先级高的先出队列。如果将代价值cost作为优先级，cost小的优先级高，那么正好代价树的宽度优先搜索中就可以使用Priority Queue来实现OPEN表，表中的元素采用元组（cost，［路径列表］）存储。由于表中的路径列表项包含了回溯路径，因此简化了CLOSED表的处理代码。用列表来实现优先级队列，其实就是在队列的基础上，增加每次向队列中添加元素后进行排序的过程。

下面所附的代码在将扩展节点添加进OPEN表中时（代码第35行），并没有检查节点是否已经在OPEN表中和判断是否需要替换的原因是为了简化代码，因为采用了优先级队列，代价值小的会排在前面，所以一定会先进入CLOSED表中，因此只需要在CLOSED表中检查节点是否已经存在，如果节点已经存在，则不做任何处理，丢弃该节点即可，效果和算法描述中的替换是一样的。

3.Python代码

完整代码如下，其中注释掉的一些print语句去掉注释后，可以帮助调试和理解代码。

以上主要介绍了盲目搜索中的宽度优先搜索、深度优先搜索、代价树的宽度优先搜索这三种常用算法。这些算法的流程是相同的，只是对于OPEN表，也就是用于存储待处理节点的表，处理策略不一样。虽然它们都比较容易编程实现，但是一般都需要知道问题的全部状态，按照某种固定规则进行搜索，对状态空间进行穷尽遍历，效率较差，没有智能性，属于弱算法。

接下来，将介绍另一类搜索算法——启发式搜索。它可以借助启发信息来提高搜索效率，就好比对于寻宝机器人，给它装上了探宝传感器，它将借助这些信息而不用盲目地查找每个地点。