宽度优先搜索算法

从前面的分析已经知道，无论是宽度优先搜索还是深度优先搜索，都是从问题的初始状态开始一步步进行搜索，扩展过程中会出现许多待处理的状态，所以需要一个OPEN表来记录这些未处理的状态。同时，已经搜索和处理过的状态从OPEN表中删除，并且需要记录下来。可以用CLOSED表来记录这些状态。除此之外，还可以借助CLOSED表来防止重试已经搜索过的状态。由于问题的求解是找从初始状态节点到目标状态节点的路径，因而通常在CLOSED表中进行处理，记录解的路径节点。

宽度优先搜索是一层层地进行扩展，每走一步可能扩展出一批节点，用OPEN表来存储新扩展出来的节点，由于需要以先扩展的先进行处理的方式来进行，即先入先出（FIFO，first input first output），因此采用队列来实现OPEN表。

下面举例来进行说明。

例3.1　对图3.5（a）所示的状态空间进行宽度优先搜索，OPEN表中节点的取出扩展次序是怎样的？

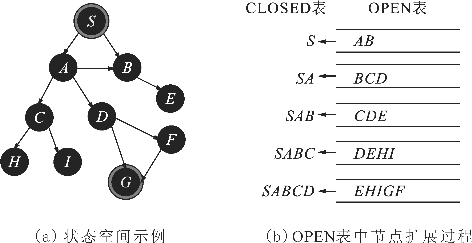
图3.5　例3.1图

解　从S出发，进行宽度优先搜索，首先将S存入OPEN表中，取出S放入CLOSED表中，S不是目标状态节点，有两条路径分别到达A和B，扩展出A，B节点，并将A，B存入OPEN表中。显然，按照宽度优先搜索的概念，这两个节点是需要先访问的。

取出OPEN表中的第一个也就是先放入的A节点，将它放入CLOSED表中，A不是目标状态节点，由A出发有3条路径——C，D和B，由于B节点已经在OPEN表中了，因而将C和D存入OPEN表中。(www.xing528.com)

接着需要取出OPEN表中的第一个节点B，将它放入CLOSED表中，并将它扩展出的节点E存入OPEN表中。

依此类推，如图3.5（b）所示，直到从OPEN表中取出G节点（为目标状态节点），所以OPEN表中的节点扩展次序依次为：S，A，B，C，D，E，H，I，G，F。

例3.1中，为了得到从S到G的路径，也就是问题的解，需要在找到G以后，由G找到其父节点D，由D找到其父节点A，再由A找到其父节点S，S的父节点可以设为空（NULL），这样就得到了解的路径S-A-D-G，所以在程序实现中扩展节点时需要记录每个节点对应的父节点。每个节点对应的父节点通常会在添加进CLOSED表中时记录。

从宽度优先搜索的过程不难发现，由于类似穷举搜索，因而如果状态空间是有限的并且包含解，则一定可以找到解，如果搜索完状态空间找不到解，则说明解不存在。用术语来说明，该算法是完备的（complete）。另外，宽度优先搜索是一层层逐层递进搜索，假设每一步的长度都是相等的，那么找到的解一定是从起点到终点的最短路径。用术语来说明，该算法是最优的（optimal）。这也可以看作是宽度优先搜索的优点之一。

再来简单看一下算法的时间复杂度和空间复杂度。假设从初始状态节点开始，每个节点有b个分支，最短的解在第s层，整个状态空间有m层，那么将要搜索的节点数为第1层b0，第2层b1，第3层b2，…，第s层bs-1，所以搜索的时间复杂度为O（bs）。对于OPEN表FIFO队列来说，最多可能需要存储某一层的所有节点，所以最多为第s层的所有节点bs-1（当第s层的最后一个节点为解时），而CLOSED表则最多可能需要存储每一层的所有节点，所以空间复杂度由CLOSED表决定，也为O（bs）。显然，这也反映出了宽度优先搜索的缺点，随着搜索深度的增加，时间复杂度和空间复杂度都呈指数级增长。

在第2章中提到的传教士与野人过河问题就可以采用宽度优先搜索这一盲目搜索方法来解决。还是以3个传教士、3个野人，小船最多能载2人为例，算符为船载人从一边到另一边，船上允许的合法人数组合［（1，0），（0，1），（1，1），（2，0），（0，2）］可以存入列表，以方便使用。

具体的搜索过程为：从初始状态节点（3，3，1）开始，船在左岸用减法，在右岸用加法，用列表中的值进行扩展，得到下一步状态节点（2，3，0）、（3，2，0）、（2，2，0）、（1，3，0）、（3，1，0），剔除不合法节点，将（3，2，0）、（2，2，0）、（3，1，0）存入OPEN表中；取（3，2，0）节点，得到下一步状态节点（4，2，1）、（3，3，1）、（4，3，1）、（5，2，1）、（3，4，1），（3，3，1）已经在CLOSED表中，其余的节点均为不合法节点，所以本步骤之后OPEN表没有变化；接着取OPEN表中的（2，2，0）节点，得到（3，2，1）、（2，3，1）、（3，3，1）、（4，2，1）、（2，4，1），将（3，2，1）存入OPEN表中；再取（3，1，0）进行扩展……直到搜索到（0，0，0）目标状态节点，从而得到解答。具体Python代码的实现过程可以参考本章后面的实验部分。