用状态空间求解问题的步骤

状态空间中的问题求解过程就是一个不断把算符作用于状态的过程。首先从初始状态开始，选择适用的算符，产生新的状态，这样继续下去，直到产生目标状态，就表示得到了问题的一个解，这个解就是由初始状态到目标状态所构成的序列。

在吃豆人游戏例子中已经解释了这个过程，下面再来看其他的例子。

例2.4　八数码拼图游戏。

请说明如何用状态空间表示法实现将图2.8中左边的拼图拼成右边的结果。

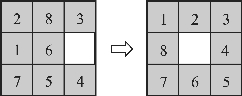
图2.8　八数码拼图游戏（一）

解　（1）本问题可以用一个3×3的数组来表示拼图状态，0表示空格。

（2）初始状态（S0）和目标状态（Sg）为：

（3）当移动一个拼图块时，一种状态就变为另一种状态了。这里借助前面介绍的产生式规则来定义算符。具体来说，空格周围的拼图块是可以移动到空格里的。一旦进行移动操作，拼图状态也就发生变化了。

每个拼图块都可能有上、下、左、右四种移动操作，产生式规则数很多，程序实现很复杂。为了简化，换一种方式考虑，用空格的移动来代替拼图块的移动。这样就可以只写出空格上、下、左、右移动的四种产生式规则即可。

如果用S［i］［j］表示第i行、第j列的数码，并用i0，j0分别表示空格所在的行和列变量，那么就可以建立如下4条产生式规则。

R1：　if（j0-1≥1）then begin S［i0］［j0］=S［i0］［j0-1］；S［i0］［j0-1］=0；j0=j0-1；end　空格左移

R1规则解释：如果空格不在第1列（其他列减1都大于或等于1），即不在最左边，那么将空格的值用它左边格子的值替换，空格左边格子值为空格值0，同时更新记录空格的列变量值，这样就实现了空格左移。

R2：　if（i0-1≥1）then begin S［i0］［j0］=S［i0-1］［j0］；S［i0-1］［j0］=0；i0=i0-1；end　空格上移

R3：　if（j0+1≤3）then begin S［i0］［j0］=S［i0］［j0+1］；S［i0］［j0+1］=0；j0=j0+1；end　空格右移

R4：　if（i0+1≤3）then begin S［i0］［j0］=S［i0+1］［j0］；S［i0+1］［j0］=0；i0=i0+1；end　空格下移

接下来，就可以考虑用产生式系统来推理求解这个问题。

目前，已经有了规则库，接下来建立综合数据库，并在综合数据库中存放初始状态、目标状态以及空格发生移动时出现的中间状态。这里，这些状态可以都用矩阵表示。

最后就是实现推理机，进行控制推理求解。

在进行推理时，可能会有多条产生式规则的条件部分和综合数据库中的已有事实相符，这样就可能激活多条规则，究竟用哪一条规则，就需要进行规则冲突解决了。

在这个例子的初始状态下，空格在第2行第3列，意味着可以左移、上移或者下移，也就是满足R1，R2，R4中的条件，如图2.9所示。究竟该启用哪一条规则，有不同的选择方法。针对本例，我们采用一个启发函数h（x），它表示节点x的状态与目标状态对应格子内容不同的格子数（没有包括目标状态空格处）。计算每一条满足条件的规则下h（x）的值，哪一条规则下h（x）的值最小就启用哪一条规则。

图2.9　基于产生式规则的状态转移

所以，我们选择R4作为启用规则。依此类推，到达目标状态的规则执行过程就是求解过程。(www.xing528.com)

例2.5　八皇后问题。

首先看一下源于国际象棋的八皇后问题的具体内容。它是由德国国际象棋棋手马克斯·贝瑟尔（Max Bezzel）于1848年提出的：在8×8的国际象棋棋盘上摆放8个皇后，使其互相之间都不能攻击，共有多少种摆法？国际象棋中的皇后可以横着、竖着、斜着走任意格，如果所走的路径上有其他棋子就可以攻击并吃掉对方，也就是说棋盘上的任意2个皇后都不能处于同一行、同一列或者同一斜线上，总共可以有多少种摆法？显然，每一行放上1个皇后，可以有8种不同的位置，解的空间为88=16 777 216。如果我们可以检查完所有这些排列组合的状态自然就可以找出问题的答案。如果有计算机，这个过程并不难，可在没有计算机的时代，这不是一件容易的事。当时柏林的象棋杂志上有多达40种不同的答案。第一个正确答案在1850年由弗朗兹·诺克（Franz Nauck）给出：92种。

解　按照前面的方法，我们用状态空间来表示这个问题。

状态空间为｛i：Col［i］｝，i=0，1，…，7，Col［i］的取值也为0，1，…，7，表示第i行的皇后放在第Col［i］列，相当于是一个8×8的数组空间。

初始状态为Col［i］=-1，i=0，1，…，7，表示每行都没有放皇后。

目标状态为Col［i］！=-1，i=0，1，…，7，表示所有行都已经放置了皇后。

状态的变换规则可以简单地设置为：从Col［0］=0开始，按照八皇后问题规则，检查Col［1］，Col［2］，…，Col［7］是否都能有合法的取值，具体来说就是在下一行找是否存在空位，也就是找下一行是否有不与之前所有行处于相同列和对角线的位置。

例2.6　传教士与野人过河问题。

有N个传教士和N个野人来到河边渡河，河岸有一条船，每次最多可以乘坐K人。无论什么时候，当野人人数超过传教士人数时，传教士会被吃掉。为传教士的安全起见，请规划摆渡方案。

解　为了简化分析过程，先讨论N=3，K=2情况，即有3个传教士和3个野人，船上最多只能载2个人。N，K取其他值的求解过程和此类似，具体求解过程用产生式系统实现。

针对具体问题进行分析。

首先确定状态变量，用三元组（M，C，B）表示河岸的状态，其中M，C分别代表某一岸上传教士和野人的人数，并定义B=1代表船在这一岸，B=0代表船不在此岸。

根据题目规则要求得到约束条件：两边岸上M≥C，船上M+C≤2。

由于传教士和野人的人数是常数，所以只需要表示出河左岸或右岸一种情况即可。我们选择左岸，并用L表示左岸。

于是问题就变成求由初始状态S（3，3，1）到目标状态G（0，0，0）的过程，而使状态改变的算符即为船载人从左岸划到右岸或从右岸划到左岸。

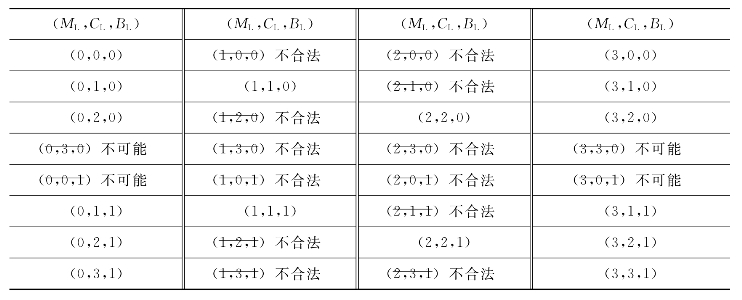
接着考虑产生式系统中的综合数据库，也就是状态空间中所有合法的状态。对于三元组（ML，CL，BL），0≤ML≤3，0≤CL≤3，BL∈｛0，1｝，可能组合出的状态空间数为4×4×2=32，但是只有M≥C的状态才是合法的，所以只有20种。另外，还有4种合法状态是不可能出现的，如表2.2所示。

表2.2　传教士与野人过河问题状态构成的综合数据库表

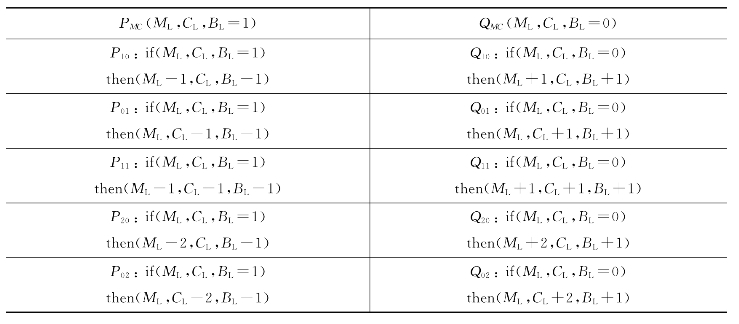
再接下来，依照产生式系统的基本结构，确定规则库。规则也对应着状态空间表示法中的算符，由船载人过河组成。如果用PMC表示船从左岸划到右岸，QMC表示船从右岸划到左岸，再加上船上合法人数的5种组合（10，01，11，20，02），可以得到10条规则，如表2.3所示。

表2.3　传教士与野人过河问题规则库表

建立了产生式系统描述之后，就可以通过控制策略，对状态空间进行搜索，求得一个摆渡序列了。接下来，引入状态转换图（见图2.10）来帮助分析。根据状态转换图在状态空间中搜索，是状态空间表示法最常用的推理方法之一，具体过程将在下一章详细介绍。

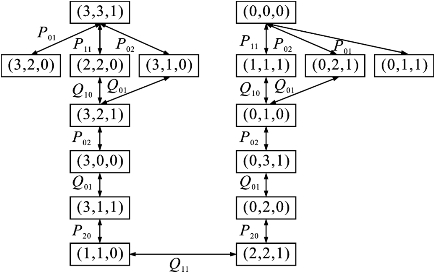
图2.10　传教士与野人过河问题状态转换图