谓词逻辑与个体域

1.谓词与个体

谓词逻辑中，原子命题被分解为谓词和个体两个部分。它不像命题以一个句子为基本单位，而是通过一个谓词来描述个体之间的关系，这样就可以对命题的各个部分进行判断、断言。另外，通过推理规则，还可以推理出新的语句。

谓词（predicate）用于刻画个体的性质、状态或个体之间的关系。个体指可以独立存在的物体，可以是抽象的，也可以是具体的。谓词逻辑中，个体既可以是常量，也可以是变量或函数，这样就能方便地建立更通用的断言。个体变量的取值范围称为个体域。比如，我们可以声明x为某一周的一天。

谓词的表示方式为：

P（x1，x2，…，xn）

P表示谓词的符号，也称谓词名。通常，人为地约定一些命名规则。一般约定，谓词用字母及以字母开头的字母数字串表示，除了下划线（_）外，其他字符不可以用，建议使用具有相应意义的英文单词，不过也可以用其他符号，比如用中文表示也行。

x1，x2，…，xn是个体，谓词中包含的个体数目称为谓词的元数，比如P（x，y）是一个二元谓词。个体是常量的谓词语句，就是原子语句。比如EQUAL（PLUS（2，3），5）就是一条值为真的原子语句。

2.谓词的语法和语句

谓词公式是用连接词、量词及圆括号将一些原子谓词连接起来的字符串。

连接词和命题逻辑中使用的连接词完全相同。

量词包括全称量词和存在量词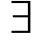两种，用来约束包含的变量的特征。x表示对于个体域中的所有（或任意一个）个体x。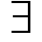x表示在个体域中存在个体x。量词的辖域为量词后面的单个谓词或者用括号括起来的谓词公式。辖域内与量词中同名的变量称为约束变量，不受约束的变量则为自由变量。

下面是一些谓词公式用法的例子：

（x）（y）FRIEND（x，y），表示对于个体域中的任何两个个体x和y，都是朋友。

如果星期一不下雨，小王会去登山。

﹁WEATHER（rain，monday）→GO（Xiaowang，mountains）

所有篮球运动员都很高。

（x）（BASKETBALL_PLAYER（x）→TALL（x））

没人喜欢考试。

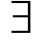﹁（x）LIKES（x，test）

3.谓词公式的性质(www.xing528.com)

谓词公式在个体域上的每一个解释都可以求出一个真值（T或F），进一步还有谓词公式永真性、可满足性（相容的）、不可满足性（不相容的、永假的）、等价性的定义。

永真蕴含：如果P→Q是永真的，则称公式P永真蕴含Q，或称Q是P的逻辑结论，P是Q的前提，记为P=＞Q。

比如，假设你喜欢的女孩对你承诺，如果你“人工智能”考试分数大于或等于0分，她就答应做你女朋友，谓词公式可以这么写，（score）GTEQ0（score）→GF（theGirl），那么就可以恭喜你，参加完“人工智能”考试，你就有女朋友了。这里其实就可以用永真蕴含的符号，因为P永远都为真。

再比如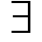，（x）（P（x）∧﹁P（x））就是永假的、不一致的。

相容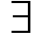：（d）P（d），也称d可满足P。

谓词公式中还有以下一些常用推论：

P相容↔（﹁P）非永真；

P不相容（P永假）↔（﹁P）永真；

P永真=＞P相容；

P不相容（P永假）=＞P非永真。

4.推理

常见的推理规则如下。

取式假言推理：P，P→Q=＞Q，表示如果P和P→Q都是真的，那么可以推断Q为真。

拒式假言推理：﹁Q，P→Q=＞﹁P，表示如果Q是假的，P→Q为真，那么可以推断P是假的，﹁P为真。

与消除：可以根据与的关系判断其中某项的真假，比如如果P∧Q为真，那么就可以推断P和Q都是真。

与引入：可以根据与语句每一项的关系判断该语句的真假，也就是如果知道P、Q都是真，那么就可以推断P∧Q为真。

全称例化（universal instantiation）：如果a来自x的定义域，那么从（x）P（x）可以推断P（a）。比如常见的三段论“所有人都会死，苏格拉底是人，所以苏格拉底会死”就是全称例化。用谓词逻辑表示就是：x（MAN（x）→MORTAL（x）），MAN（Socrates），MAN（Socrates）→MORTAL（Socrates）。

合一（unification）算法：可以被自动问题求解器用来将用全称量词修饰的x替换为它的一个实例，比如上例中的Socrates。它是一种判断什么样的替换可以使产生的两个谓词演算表达式匹配的算法。

为了做到这一点，要求所有的变量都是全称量化变量，这样才能允许在计算替代时有完全的自由度。如果有存在量化变量，就要想办法消除，通常采用的消除方法是用使这个语句为真的常量来代替它。