金属材料的热膨胀及其关系的解析

金属和大多数物质一样存在热胀冷缩现象，但是比橡胶和塑料小一些。在通常情况下，金属材料的伸长与温度关系可用经验公式来表示：

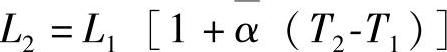或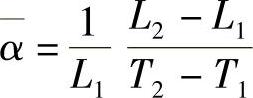

式中 L₂、L₁——分别为温度T₂、T₁时金属的长度；

α——在温度T₂、T₁之间平均线膨胀系数。

当温度与长度的变化趋于零时，

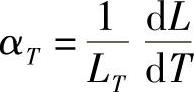
α_T称为温度为T时真线膨胀系数。

对于给定的材料，只要得到L=f（T）的曲线，便可在曲线上找出L_T及该点的微分，并算出α_T的数值。(www.xing528.com)

对于某一材料，α不是定值（常数），随温度略有变化，实际上应用的膨胀系数，多为某一温度范围内的平均值。

金属和合金的热膨胀，是由于原子间距增大的结果。这是由于当温度升高时，金属原子或金属离子，在整个金属的振动并非简谐振动，而具有不对称性。其距离在两个方向上并不相等，这就造成了整个金属的伸长。

以双原子模型为例进行定性分析：如图2-9所示，两个相邻原子，一个原子不动，另一个原子相对第一个原子振动。当振动的原子通过其平衡位置时，势能W为0，这时原子只有动能。随着原子离开平衡位置越远，其势能越高动能越小。当温度为T₁、T₂、…时，对应的势能为W₁、W₂、…，在每一温度下，两原子距离r存在两个临界值。W₅对应T₅温度时的势能，r₁、r₂分别表示在T₅时两原子接近及远离时的距离，a₅为两个原子的平均距离。r₁、r₂、…各中点的连线表示温度不同时两原子平均位置的变化。很明显，当温度升高时，原子振幅增加，势能增高，振动中心向右偏移。结果必然导致原子间距离增大。由于原子间距离的增大，宏观上表示金属长度的增加。

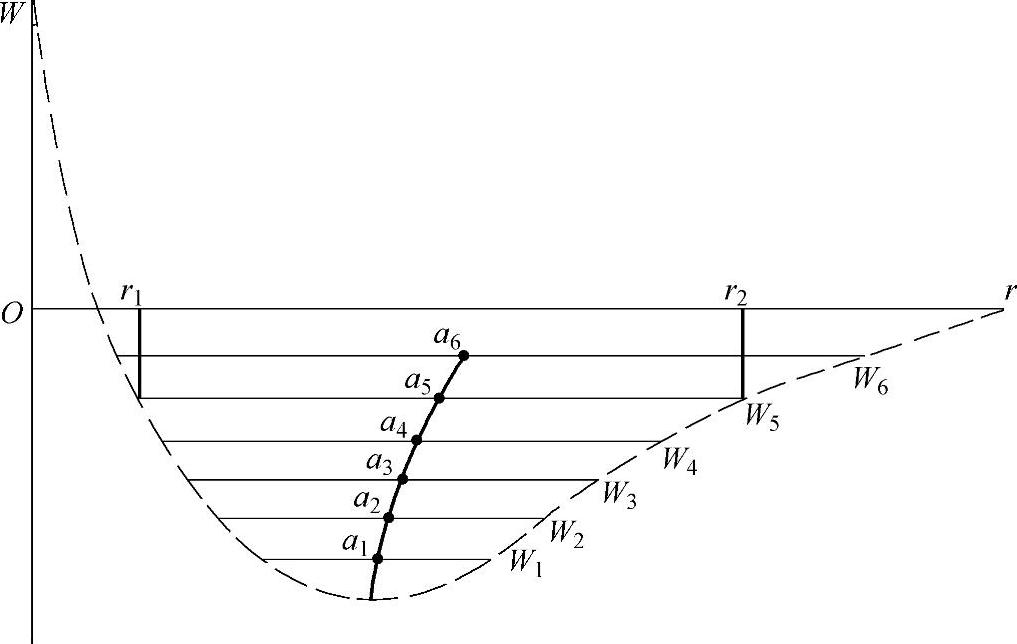
图2-9 原子间相互作用的内能曲线

在一般情况下，金属的长度随温度升高的增大是呈线形的，但当金属出现相变时，膨胀系数发生剧变。与此同时，金属的比容（即单位质量的体积）也会发生相应变化。比容的变化规律与膨胀的变化规律是一样的。金属线膨胀系数比橡胶和塑料小，一般为10^-5～10^-6/K。