摩尔热容(Cm)的定义和计算

一摩尔物质升高1K所需的热量称摩尔热容。金属的摩尔热容是1克原子金属升高1K（度）所需的热量又称为金属的原子热容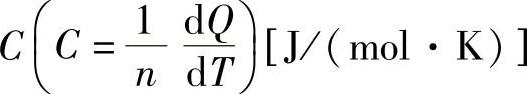。显然，数值上等于金属比热容和原子量A的乘积：

C_V=c_VA或C_p=c_PA

根据单原子理想气体的分子热容动力学原理，理想气体在运动时，只有平动的动能，属于一个自由度的平均动能为，由于在三个自由度下，故动能等于。在固体中确定热容，不仅要考虑动能，还要考虑振动着的原子位能。位能又等于动能，总的能量为3kNT。

因此，1g原子的内能应等于3kNT，即

U=3kNT

故，固体的原子热容为

这表明，克原子的热容是常数，数值等于24.9J/mol·K，这就是杜隆-珀替定律。

但是，固体的摩尔热容实验事实如下：

1）在室温范围内，几乎所有单原子固体（包括金属）热容的值接近于3R即24.9J/mol·K，这与杜隆-珀替定律一致。

2）在低温下，固体的热容显著下降，对于绝缘体，依T³趋于0。对于金属按T趋于0，或更确切是C_V=γT+AT³（γ、A与材料有关的常数）。

显然在低温下，固体金属的原子热容并不是常数，而是与温度有关，温度越低，热容越低。

为了确定固体低温下的热容，费米提出了费米模型，推出金属的热容为

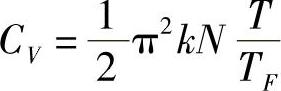
式中 T_F——费米温度，与物质本性有关的常数。应当指出利用费米模型推导金属热容时，只考虑了自由电子对热容的贡献。(www.xing528.com)

1912年德拜提出德拜模型，推导出了晶体的热容公式：

式中 θ_D——德拜特征温度，决定于晶体物质的本性。

当T≫θ_D时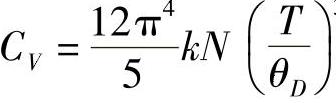：，即温度很低时，晶体的热容与温度的三次方成正比，这就是德拜定理。

当T≪θ_D时：C_V=3kN，这与杜隆-珀替定律一致。

同样应当指出，在德拜模型中没有考虑电子对热容的贡献。在很低的温度下，电子的热容不像离子（或原子振动）热容急剧衰减。在温度比德拜温度和费米温度低得多的情况下，金属的热容是电子热容和离子热容的两者贡献之和，即

C_V=rT+AT³

式中 r、A——标志材料特征的参数。

上式中，第一项为自由电子对热容的贡献，与T成线形关系，可由费米公式计算出来，并且在足够低的温度下占主要地位。第二项为金属离子（或原子振动）对热容的贡献，与T³成正比，可由德拜公式计算出来。由于费米温度比德拜温度高约两个数量级，所以只有在极低的温度下，金属的比热容与T成线形关系。例如低温时：

C_Cu=0.888×10^-4RT+C_V′

C_AL=1.742×10^-4RT+C_V′

在很宽的温度范围内，金属摩尔热容随温度的变化基本可分为三个区域。当温度接近0K时，金属摩尔热容与温度呈正比；当温度较高时，金属摩尔热容与温度无关，近似等于3R（见图2-8）。

图2-8 铜的摩尔热容随温度的变化曲线