前导序列长度素数设置下的最佳互相关特性分析及应用

Zadoff-Chu序列^[15]属于CAZAC，它可用作RACH前导序列，原因在于它具有如下良好的序列属性：

1）Zadoff-Chu序列拥有值为0（包括零偏移值）的周期性自相关函数。这对于前导检测和定时估计是非常重要的。此外，某个序列的循环移位是相互正交的。因此，多个前导序列可以通过具有循环移位的单个Zadoff-Chu序列得到。

2）由于前导序列长度被设置为一个素数（即839），因而存在着838个具有最佳互相关特性的序列。

3）序列还具有较为合理的立方量度特性。

不同前导所使用的循环移位之间应有比较明显的分界线。循环移位分界线需要足够宽，以满足上行链路定时不确定性的需要，如图5-32所示。传输时延和循环移位分界线与蜂窝覆盖范围之间存在着直接的关系。为满足LTE所支持的较大蜂窝覆盖范围要求，每个蜂窝可配置16条不同的循环移位分界线，由单个Zadoff-Chu序列提供第1～64个前导序列。

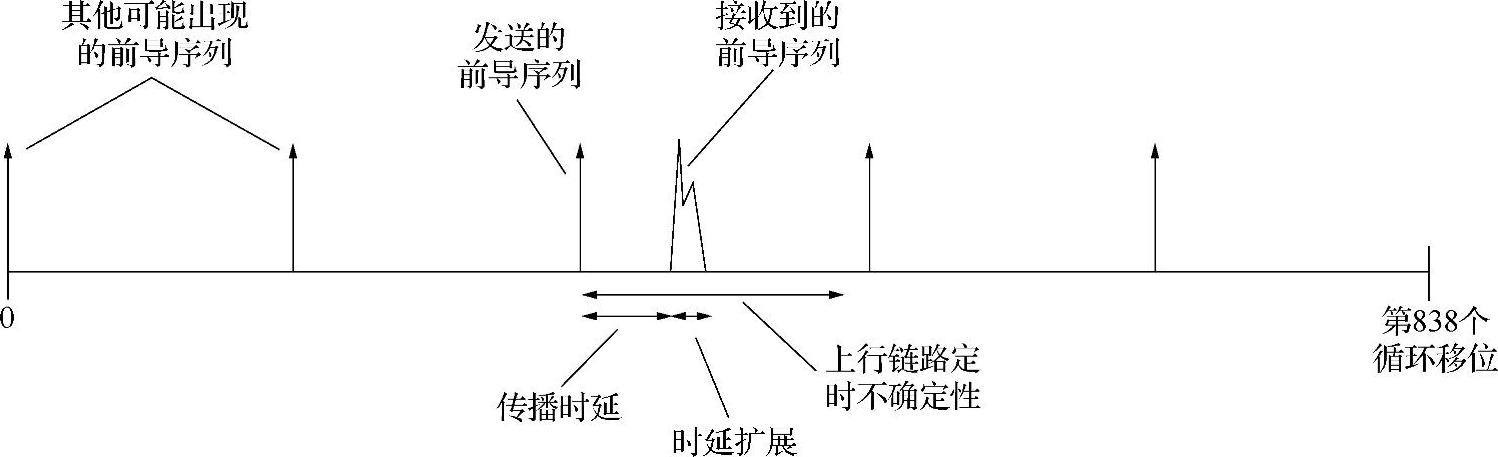
图5-32 前导序列之间的循环移位分界线NCS

针对多普勒扩展，由于Zadoff-Chu序列具有特殊性质，所以RACH定义了一种特殊的高速模式或限制集。从本质上讲，高速模式是为循环移位定义的一系列附加限制条件，这些循环移位可用作前导序列。

Zadoff-Chu序列的离散傅里叶变换（DFT）也是一个在频域中定义的Zadoff-Chu序列。由于存在多普勒扩展，传输的前导序列在频域内与发送的循环移位相邻的循环移位上进行扩展，尤其是在频域内与发送的循环移位直接相邻的循环移位上进行扩展。尤其需要指出的是，与序列长度倒数对应的多普勒频率（对于LTE来说，该频率为1.25kHz），将序列中待发送的循环移位完全转换为频域内与发送的循环移位直接相邻的循环移位。这样，接收到的序列与多普勒频率为1.25kHz的发送序列是正交的。(www.xing528.com)

频域内直接相邻的循环移位之间存在着简单的一对一关系，时域内直接相邻的循环移位之间也存在着这种关系。因此，针对某个前导序列，可以定义3个上行链路定时不确定性窗口，这些窗口是由如图5-33所示的漂移距离来分开的。漂移距离是Zadoff-Chu序列索引号的函数，定时不确定性窗口的漂移是循环进行的，如图5-33所示。

图5-33 具有明显多普勒频移的、RACH前导序列的上行链路定时不确定性窗口

如前所述，当检测到前导序列存在明显多普勒频移时，会推出如下结果：

1）信号能量需要从所有3个窗口处聚集，以确保前导序列检测可靠进行。

2）考虑到初始上行链路定时估计，前导序列的窗口不应当互相叠加。

3）不同前导序列的窗口不应当互相叠加，以防止不必要的假警报。

因此，高速模式下的前导序列循环移位，需要进行选择，以确保每个定时不确定性窗口以及窗口之间不互相叠加。虽然这些要求以及漂移距离与序列索引号之间的关系，使得前导序列的循环移位计算变得复杂，但是人们已经提出了较为简单的等式，并对其进行了标准化^[18]。