Bootlace透镜多波束形成器优化顶部表现

固体介质透镜的权因子通过透镜分区处理来实现。早期的工作模式以模拟方式来处理介质透镜，基本的透镜形成器分为三种即Ruze 透镜、Bootlace 透镜和Rotma 透镜。其中，Ruze透镜包含了透镜内平行于轴的射线的传播，比如图8.16 中的PQ 通路可由多种途径形成，如波导、同轴线、三板带状或微带线。电长度PQ随着与透镜纵轴y 的交点的变化而产生。利用通过点P 和Q 及透镜原点的射线轨迹，联立方程解出透镜厚度和折射率，并限定内轮廓为椭圆。此时假定F1、F2为仅有的两个焦点。对于一般的C 点，其像差相位或偏离透镜平面波前的路程差可以用以y 为变量的多项式表示。其中对于长焦距透镜，高于y3 的项可忽略。将C 沿径向朝着或背离透镜方向移动，如二次聚焦一样，可降低相位误差。增加透镜焦距也可减小像差。假设透镜连线不再与轴平行，如图8.16 中的PO′所示，这构成了Bootlace 透镜，它扩展了平板表面。Ruze 透镜设计有三个可变参数，即透镜轮廓、厚度和折射率，Bootlace 透镜引入了第四个参数，即前后单元的相对间距。折射率由PO′长度决定。这第四个额外参数使得第三个准确焦点存在，即透镜轴（-G，O）点，这样进一步降低了透镜像差。G 的选择是使在Ruze 透镜的二次聚焦中相位误差最小。对于一个有特殊扫描要求的透镜，如做完善的定义，需对F1和F2的张角及归一化焦距G/F进行限定。α 通常是所需的最大扫描角，因为相位误差在± α 之间达到最小，而在此范围之外则增加很快。幅度控制及多次反射主要依赖于轮廓形状，采用两边相同的轮廓形状，并允许透镜的两边轮廓间的中心线分开。阵列可以是直线阵或为曲线阵，在聚焦弧上有三个焦点的是Bootlace 透镜。如果透镜的聚焦弧为圆弧线，两轮廓线就不相同，这种透镜称为Rotman 透镜。这里讨论带Bootlace 透镜形成器多波束发射天线阵。

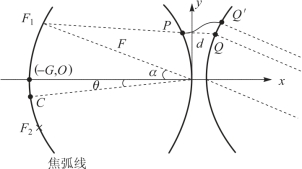
图8.16　约束透镜的几何图

当多波束天线用于发射阵时，提高合成功率是最重要的指标之一。通常采用直线阵而不采用弧形阵，这是因为弧形阵由于辐射元的方向不一致而会使合成效率下降。减小辐射元的馈电相位误差可提高合成功率，在诸多平面透镜中，Bootlace 透镜具有比较小的口径相差。整个多波束发射天线阵包括：①波束口，用来将干扰信号传入透镜；②变异Bootlace 透镜，用来对直线阵提供特定的幅度相位分布，以在空间规定方向上产生波束；③阵元口，为行波管放大器的输入端口提供接口；④连接电缆，将阵元口和辐射元连接起来；⑤辐射元，将干扰射频信号向指定方向辐射出去。

透镜馈电多波束天线阵是利用透镜的聚焦原理制成的，图8.17 所示为其工作原理图。其中Σ1为馈电弧，Σ2为聚焦弧，W 为补偿电缆，PQ 为直线阵。当一点源由馈电弧Σ1的点1 馈电时，波由聚焦弧上的接收元1，2，…，N 所接收，经补偿电缆W1，W2，…，Wi，…，Wn传至直线阵的辐射元且辐射出去的将是平面波，其波阵面与阵口径面成α 角，于是形成指向α 的波束1。当馈源在馈电弧上移动时，波束指向也随之移动。当馈源移动至点M0时，便形成波束M0。如果在馈电弧Σ1上按需要设置M0个馈电点，那么，在空间就可形成M0个并行波束。为了抑制栅瓣的出现，均匀直线阵的元间距通常取为1/2λmin（λmin为最小工作波长），在一定范围内增大阵元间距可以提高阵的增益。但是，如果波束数保持不变，则会使波束交点电平降低，这无疑会使交点处的干扰功率下降。增加波束数可以抵消这一趋势，但又会使开关矩阵变得复杂，工程中一般取

图8.17　透镜的工作原理图

为了提高辐射功率，要尽可能使口径D 大一些，但还要照顾到仰角覆盖范围。假设在f=18 GHz 时的3 dB 波束宽度大于20°，据此可以求得

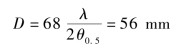
当辐射元的口径为56 mm ×8 mm 时，理论增益系数为8.34 （余弦分布）。考虑到脊喇叭的口径利用系数比光波导喇叭的低，还有驻波引起的反射损耗，取单元的增益系数为

发射阵的等效辐射功率为

式中　P0——单个行波管放大器的发射功率；

　　　g——辐射元的增益；

　　　N——辐射元的数目；

　　　η——合成效率。

若等效辐射功率为100 kW，当P0=50 W，g=2.5，η=0.7 时，可得到N=34，工程中取N=35。波束数的选取原则是：在频带的高端，波束交点电平不要太低，在8～18 GHz 频带内，交点电平不要低于4 dB，因为如果交点电平过低，会降低交电平处的干扰功率，必须增加波束数目。根据上述原则，取波束数为32，即M0=32。方向图的3 dB 宽度角在扫描角为0°的情况下，则

当f= 8 GHz 时，2θ0.5= 5.46°；当f= 13 GHz 时，2θ0.5= 3.46°；当f=18 GHz 时，2θ0.5=2.43°。当波束数为32，覆盖角为±45°时，标称波束宽度为2.812 5°。显然，当N=32 时可满足要求。当波束扫描时，波束宽度由式（8.68）求出的数值再除以扫描因子cos θk（θk为波束扫描角）。当θk=45°时，8 GHz、13 GHz、18 GHz 相对应的波束宽度分别为7.72°、4.89°、3.44°。假设在±45°内均布32个波束，则每个波束占有角度宽度为90°/32=2.812 5°。此波束位于扫描角为0°的位置上，则与相邻波束的交点为45°/32=1.406°，将此角度值代入，由

可求出交点电平e。

当f=8 GHz 时，e=-0.76 dB；当f=13 GHz 时，e=-2.08 dB；当f=18 GHz 时，e=-8.72 dB。直线阵的一个特点是当波束扫描时，随着扫描角的增大，辐射功率会降低。这有两方面原因：一是波束增益随扫描角θk的增大而cos θk的变化小；二是单元方向图在θk位置低于0°方向上的值，故当波束扫描到θk时，功率迭落电平为

实际上，随着波束扫描角的增大，对阵口径的照射变得越来越不均匀，这会引起增益下降，并且随着频率的增高，馈源对阵口径边缘的照射电平会降低，这无疑会降低口径利用系数，也会引起边缘波束增益迭落。因此，边缘波束增益的实际迭落比上面计算的大一些。透镜是多波束发射阵的核心部件，合理地设计透镜对发射阵的性能有着决定性的影响。

在Bootlace 平面透镜中引入一个新的参数m，可使原透镜变得更具灵活性，这样得到的透镜称为变异Bootlace 透镜。当m=1 时，变异Bootlace 透镜便成了原Bootlace 透镜。变异Bootlace 透镜如图8.18 所示，Σ1为馈电弧，Σ2为聚焦弧，Σ1和Σ2为完全相同的曲线；点F0（0，2A-C）为y 轴方向，F1（m，A）、F2（-m，A）为偏轴焦点；A、C 为待定常数；m、θm确定透镜结构的参数；xOy为透镜的直角坐标系；z 为阵口径坐标轴。透镜的轮廓线方程为

图8.18　变异Bootlace 透镜

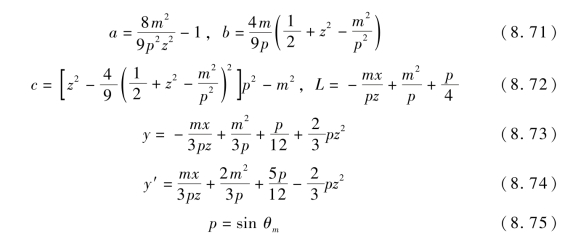
式中　θm——馈源位于偏轴理想焦点时的波束扫描角。

常数A 和C 及2A-C 的值为

式中　T——透镜的厚度。(www.xing528.com)

由式（8.71）、式 （8.72）、式 （8.73）、式 （8.74）可见，透镜的轮廓仅取决于参数m 和θm。假设有一馈源位于点F（xF，yF），该点所对应的阵口径坐标zF与该点的波束扫描角θ 及偏轴理想焦点的波束扫描角θm的关系为

当给定波束扫描角θ 时，由式 （8.76）可求出zF，再按 （8.71）求出xF。按式 （8.73）求出yF，则点F 被确定。对于馈电三角和接收三角的口径，假设在焦点F1和F2之间的弧线上均匀分布M0个馈源，则每个馈源的口径为

接收元的口径D 也按式（8.77）计算，只是将波束数M0换为N。前面所述的透镜为归一化透镜，即用阵口径去除以透镜的所有尺寸而得到透镜尺寸。要得到实际透镜，就要将上述各公式得到的数值乘以归一化系数kg。令

式中　εr——制作透镜的材料的相对介电常数；

　　　N——阵元数；

　　　d——元间距。

当N=35，d=10，εr=2.2 时，kg=235.97。无论是馈电三角元还是接收三角元，由透镜轮廓线的口径到波束口或阵元口的50 Ω 微带线，均可看成一阻抗渐变段。选择这一渐变段的长度除了考虑反射系数外，还要考虑两相邻波束口宽度，或阵元口之间的最小距离。这一最小距离要保证电缆头能够接到透镜的SMA 座上，反射系数为

式中　Zi——将微带渐变段分为相等的N 段，其中第i 段的特性阻抗；

　　　H——渐变线的长度；

　　　N——变换段的分段数，N 越大，计算精度越高；

　　　α——波数，α=2π/λ，λ 为工作波长。

当馈电三角口径为10.11 mm，50 Ω 微带线宽度为2.8 mm，变换段长度H=1.6，λmax=60 mm，εr=2.2 时，按式 （8.79）计算的驻波系数S=1.13。取实际透镜的馈电三角的长度H=40.5 mm。当偏轴馈电时，对阵口径的照射将产生不对称现象，扫描角越大，这种不对称现象越严重。由于偏轴馈电时透镜的口径场幅度分布的计算公式比较繁杂，这里只给出计算结果。当扫描角θm=45°时，口径左右边缘的幅度比大约为0.9 ∶0.2。这一计算结果是假定三角的高与三角口径中心处透镜轮廓线的法线重合得到的，显然，改变三角的指向（口径中心不变），可改变三角的辐射方向图，从而可调整对阵口径的照射情况。结果表明，这种方法可使不均匀照射的比变到约0.6 ∶0.4。在透镜中，它的口径相位误差分为固有误差和制造误差两种，固有相位误差是透镜所固有的。当透镜的参数θm、m 及阵口径Nd 确定后，固有相位误差是一个常数。当θm=45°，m=1.25，Nd=350 mm，f=18 GHz 时，固有相位误差约为4°。这样的相位误差对方向图的影响可完全忽略不计。

为了加工方便，将透镜的输出/输入端口插座所在的轮廓设置为圆，否则，将使加工大大复杂化。按照透镜的聚焦方程波由点F0到Σ2上的A′再到Σ3再到A 与由F0到Σ2上的B′再到Σ3上的B 之间的路径长度应当相等。在计算路径长度时，通常将几何长度A′A 和B′B 当成电长度计算。实际上，三角微带渐变段的电长度与几何长度是不相等的。这是由于微带线有等效介电常数，而它又是阻抗的函数，所以，要严格计算三角的介电常数是困难的，但可用数值法近似计算。即将三角分为许多小段，将每一小段电长度求出来，再累积起来，则可求出三角的电长度，从而可以求出相位误差。

上述由于简化设计带来的相位误差可以进行修正，由图8.19 可见，在不改变B′的位置时，将Σ3圆的圆心在F0A 轴上移动，则通过改变B′B 的长度，从而改变相位误差。计算表明，圆心移到某一位置，可将上述制造误差基本上消除，即最大相位误差超过1°。对于发射天线阵，它所承载的功率取决于发射天线各部件的击穿功率。对于透镜馈电多波束天线而言，由于行波管加在透镜和辐射元之间，因而只需连接同轴线和辐射元的击穿功率。同轴线的击穿功率为

图8.19　透镜轮廓线

式中　S——驻波系数；

　　　Vm——击穿电压；

　　　Z0——特性阻抗。

当采用SFT-50-3 型半硬同轴线时，特性阻抗为50 Ω，Vm=5 kW。假设驻波系数为4，则Pmax=62.5 kW，高于行波管的发射功率。由于辐射元采用脊喇叭，在馈电处为微带线，辐射元的击穿功率便取决于馈电微带线的击穿功率。当h=0.5 mm （微带到地板之间的距离）、t= 0.01 mm （t 为条带的厚度）、εr=2.6、温度为20 ℃时，功率见表8.4。

表8.4　最大承受功率

根据上述Pmax随频率下降的趋势，估计当f=18 GHz 时，如果驻波系数是4，则Pmax=67.5 W，仍大于行波管的发射功率50 W。当εr或h 增大时，Pmax也将增大。但随着温度升高和压力的降低，击穿电压会下降，其关系如下：

式中　p——大气压力（Pa）；

　　　T——热力学温度；

　　　Pmax——在标准大气压下温度为20 ℃时计算值。

当环境温度为60 ℃时 （p 为标准大气压），按式 （8.81）计算的=258 W （h=0.5 mm，εr=2.6，f=15 GHz），仍可承受50 W 的发射功率。由于天线的性能与影响天线性能的各种参数大多是复杂的隐函数关系，不可能找到简单的优化设计方法。因此，经过大量的分析、计算和相关的试验，应用改进型的Bootlace 透镜于多元阵列，突破了馈电弧间的相互影响，很好地解决了杂散波在左右边缘的匹配问题，成功地研制出了宽带较大型的波束天线阵，典型方向图如图8.20 所示。带有多波束发射天线阵的系统，具有对付多目标和能合成空间大功率的能力，同时具有工作频带宽、瞬时压制范围大、可靠性高、反应速度快等特点。

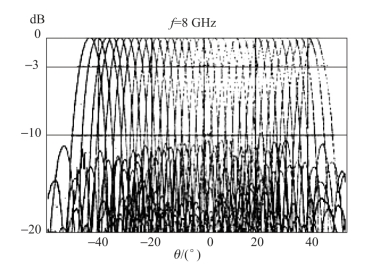
图8.20　典型的多波束辐射图