小孔径宽带Adcock天线阵设计原理与应用

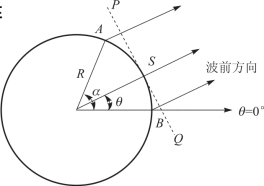
图8.4　全向圆阵示意图

图8.4 所示为全向元连续分布圆阵示意图。其中，R 为阵半径，θ 为波前PQ的法线方向 （简称波前方向），α 为任一阵元A 与阵元B 所夹圆弧的张角，阵元B所在的直径与θ= 0°方位的方位射线重合。

若以通过阵直径方位射线上的阵元S为参考点，任意阵元A 的激励电流为

按几何光学理论，阵元A 辐射至波前平面PQ 的电场相位为

式中，k=2π/λ，λ 为波长。

由此得圆阵的远场方向图函数为

根据柱函数理论，有

对照式（8.12），得

将相位参考点从图8.4 中的S 点移到圆心，则

式（8.13）就是全向元连续分布圆阵K 次相位模的表达式。

当圆阵的全向元为均匀离散分布时，其阵元激励可看作连续分布的取样激励。根据取样定理，只要圆周取样率比圆阵激励相位在圆周上的周期数 （K值）大得多，那么阵元离散分布圆阵便能良好地再现阵元连续分布圆阵的电性能，即其方向图仍可用式 （8.12）来表达。事实上，当离散分布阵元的激励电流为

式中　i——阵元序号，i=0，1，2，3，…，N-1；

　　　N——阵元数。

其电场方向图为

考虑到在我们研究的问题中，，故式 （8.14）中的第二项远小于第一项，略去第二项，得

显然，式（8.15）与式 （8.13）的表示形式相同，因此，式 （8.15）为全向元离散分布圆阵的K 次相位模表示式。

0 次模和1 次模形成正余弦信号的基本原理如下。

当K=0 和1 时，由式（8.15），得

由式（8.16）、式（8.17）可见，0 次模的振幅比1 次模大得多 （kR≪1），这就是全向元DBD （数字鉴相器）天线阵与有向元 （通常只在高频段才能实现）DBD 天线阵的主要区别（有向元DBD 天线阵各可用相位模的振幅均接近相等）。将0 次模的幅度进行适当衰减，使其振幅等于1 次模的振幅，再将1 次模的信号移相φ，然后将两者输入同一相加网络，得到合成信号为

247 式中，A=NJ1（kR）。

令φ=0 和π，并将所得信息做平方律检波相减，得

同样，再令φ=，有

若取N=8 （8 元圆阵），注意到kR≪1，利用一阶贝塞尔函数的级数表示式为

略去kR 三次以上的微小项，式（8.19）和式（8.20）可简化为

鉴相器对输入的两路信号中的一路具有移相0、π/2、π、3 π/2 的功能。故式（8.21）、式（8.22）就是电平相等的0、1 次模输入同一鉴相器后，再将四个输出信号两两相减所得的结果。将式（8.21）与式（8.22）相比较，可得(www.xing528.com)

众所周知，偶极子天线在E 面的方向图为“”形，而H 面方向图则具有全向性。Adcock 曾提出两个反向馈电偶极子组成二元阵的方法来获得“”形的H 面方向图。利用由8个全向元单极子或偶极子组成的圆形阵列，通过馈电网络的变换作用，该天线阵包含两组反向馈电的全向元 （每组有三对反向馈电的全向元），在方位面内各形成一个“”形H 面方向图，且两者在H 面内互相正交，改善了宽频带角鉴别能力。由于该天线的测角方法仍以“”形H 面方向图为基础，习惯上仍称为Adcock 天线 （以小口径测向天线阵发明人Adcock 命名）。

8 元Adcock 天线阵如图8.5 所示，由8个宽带单极子（或偶极子）和一个馈电网络组成。图中F0（θ）显然就是8.1 节中的0 次相位模，而Fs（θ）和Fc（θ）则为相互正交的“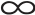”形H 面方向图，其各方向图对应阵元的等幅激励相位见表8.2。

表8.2　对应阵元的等幅激励相位

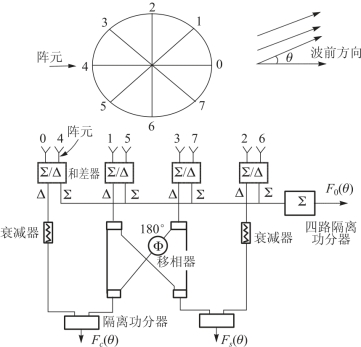
图8.5　8 元Adcock 天线阵构成示意图

根据图8.5 和表8.2，得

注意到kR≪1，将式（8.24）、式（8.25）、式（8.26）用泰勒级数展开，略去三次以上的高次项，得

显然F0（θ）具有全向性，Fs（θ）和Fc（θ）为两个正交的“”形方向图，且F0（θ）的振幅远大于Fs（θ）和Fc（θ）。

F0（θ）、Fs（θ）和Fc（θ）形成正余弦信号的原理如下。

设在F0（θ）信道中引入适当的衰减量η，使

再在两路信道中的一路引入的移相量 （可用正交耦合器实现），则有合成信号为

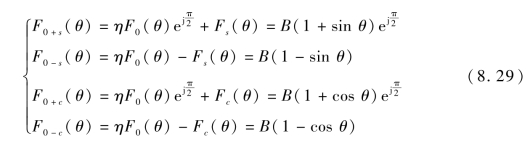
将式（8.29）中的四式表示的信号做平方律检波相减，得

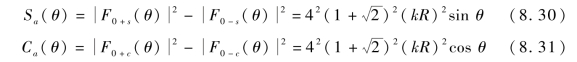
以上从基本原理出发，求得了各电压方向图的表示式，还给出了用于量化编码的正余弦函数，以下基于这些表达式进行讨论。

式（8.21）、式（8.22）、式 （8.25）和式 （8.31）表明，正余弦信号的形状与kR 无关，即与工作频率及阵列半径无关，从而原则上可设计出阵列半径非常小的圆阵，而并不影响测向性能。但是，随着阵列半径变小，阵元间距也越小，阵元间的互耦势必变强，从而影响阵列的性能，因此，最小阵列半径主要取决于阵元间的互耦情况。

设阵元的增益为0 dBi （全向元），因0 次模的振幅图是无方向性，故避开用空间积分求增益的方法，就可以确定0 次模的增益为0 dBi。于是，与8 元DBD 天线阵的正余弦信号相对应的增益为

与8 元Adcock 天线阵正余弦信号相对应的增益为

这两种天线阵的增益都是很低的，为了保证系统灵敏度，要求接收机具有尽可能高的灵敏度。对于圆阵中的阵元数，由式 （8.21）、式 （8.22）、式（8.30）和式（8.31），并根据式 （8.15）求得，即在求解中对所用的Fd（θ，0）=F0（θ）及Fd（θ，1）的表示式做了近似处理。根据柱函数理论，阵元数目越多，式 （8.15）的近似程度越好，反之亦然。但N 越大，系统太复杂，实际上，折中考虑后取8 元阵为宜。当然，如果可以降低天线阵列的电气指标，也可采用更少的阵元数目。

DBD 天线阵的馈电网络比Adcock 天线阵的馈电网络要复杂一些，又由式（8.21）、式（8.22）、式（8.30）和式（8.31）可知，以0、1 次模为基础的DBD 天线阵与Adcock 天线阵具有相同的测向性能，故采用Adcock 天线阵要更合适些。但对于Adcock 天线阵而言，当馈电网络的电性能给定后，其极限测向精度也就被确定了。

要进一步提高测向精度，上述两种体制均有一定的限制，需用大间距的干涉仪或大半径圆阵的多普勒体制。这两种阵列在电小尺寸情况下，在测向精度方面体现了它的优势。因为这两种体制原则上仍以比相为基础。对干涉仪而言，相位与方位角的关系为kdsin θ （d 为阵元间距），当d 小于半波长时，方位角变化360°，相位变化则小于360°。对多普勒体制而言，若以圆心上的天线作为参考，则相位与方位角的关系为

式中　i——阵元序号；

　　　N——阵元数。

当R 小于半波长时，固定方位角θ、i 由开关自0 顺序依次接至N-1，其相位变化也小于360°。而Adcock 天线，方位变化360°，则相当于相位变化360°。关于0 次模的衰减量，在F（θ，0）、F（θ，1）通过鉴相器形成正余弦信号中，由于鉴相器和正交耦合器固有的相位误差、反射和不完善的隔离，所以，只有当两路待鉴相的信号振幅相等时，才有最高的鉴相精度。因此，这里介绍的天线阵列均要求接收机具有随频率自动更换0 次模衰减量的功能 （振幅跟踪），使输入鉴相器或正交耦合器的2 倍信号具有相等的振幅。当然，鉴相器和正交耦合器的性能越好，接收机振幅跟踪的精度就可降得越低。事实上，对理想鉴相器和理想正交耦合器而言，接收机的振幅跟踪可不做要求，因为不衰减0 次模而利用式 （8.16）、式 （8.17）、式 （8.18）和式 （8.27）、式 （8.28）、式（8.29）也可得到正余弦信号。为了工程中实现的方便性，在图8.5 中采用四个反相功率分配器及在阵列中心设置一个阵元天线来代替和差器及一个四路隔离功率合成器，从而网络中的部件减至三种，即二路隔离功率分配器、6 dB 衰减器和反射的隔离功分器。

整个天线阵采用宽带的单极子天线作为阵元，考虑到天线之间的互耦影响，圆周半径越小，互耦就越强，且对圆周上各个单元来说是与位置无关的。经过理论分析和相应试验研究，确定8个阵元均匀分布在半径为20 cm 的圆周上，一个天线位于阵中心，单极子高度为220 mm，天线及微波部件之间用相位一致性相连。反相隔离功率器和隔离功分器结构形式相同，只是在其内部有一反相部件。为了满足宽带工作，采用的微波器件都必须具有宽带特性，对于功分器设计，采用三级二路功分器，图8.6 中几何长度为

式中　εe——微带线的有效介电常数。

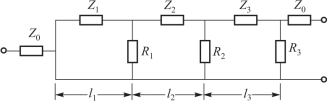
图8.6　功分器电路结构图

采用聚四氟乙烯双面覆铜板制作，功分器部分的电路形式为微带线及平板的过渡形式，如果要求等幅反相输出，可以巧妙地将平板线从结构上反转后相接。另外，3 dB 定向耦合器采用对称三级1/4 波长耦合器，其偶模阻抗取值为Ze1=1.21，Ze2=3.41。为减小体积和相邻线之间的相互影响，在功分器和耦合器中采用开槽折线方式实现。衰减器采用集中元件的Π 形网络。为使得每路的相位同相，加入补偿线，以保持通道的相位好的跟踪特性；幅度方面相对容易些。除了整个设计外，调试工作也十分必要。如图8.7 所示，宽带单极子天线阵工作于3 ∶1 频率范围内可以得到比较好的测向精度。

图8.7　宽带单极子Adcock 天线阵