分析计算星载SAR干扰的有效区域

对星载SAR 的干扰有效区与对机载SAR 的干扰有效区有许多类似之处，只不过星载SAR 飞行高度更高，探测成像范围更广，干扰所需的等效干扰功率增大。

对星载SAR 的干扰示意图如图6.27 所示。

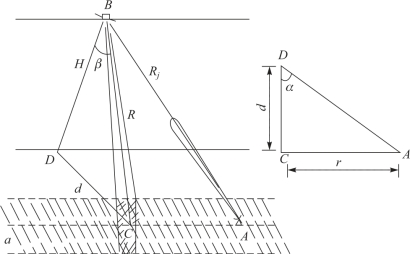
图6.27　对星载SAR 干扰示意图

A—干扰机位置；B—星载SAR 位置；C—星载SAR 主瓣区测像中心；D—星载SAR 投影点。

把图6.27 绘制成几何图形，如图6.28 所示。

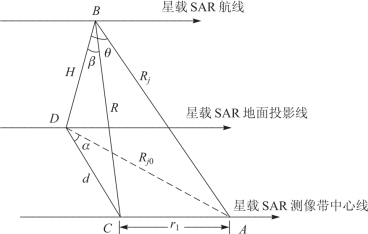
图6.28　星载SAR 干扰几何图形

H—卫星高度；Rj—干扰机与雷达的距离。

根据图6.28 可列出下列方程

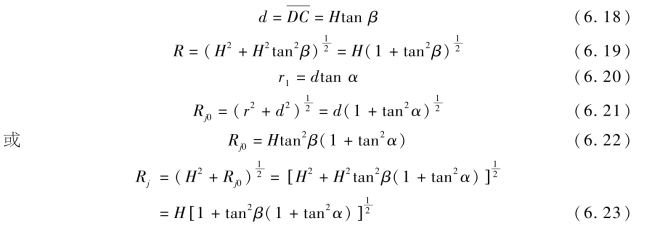
根据雷达干扰方程，有

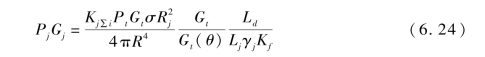
将式（6.18）、式（6.22）代入式（6.24），得

式中，Kj∑i为干扰SAR 所得的干扰压制系数，Kj∑i有两种算法：如果σ 为雷达分辨区的等效RCS，Kj∑i为二维压缩得益系数；如果σ 为雷达天线主瓣区的照射等效RCS，Kj∑i为距离压缩得益系数。这两种算法不论取哪一种，算得结果Kj∑i=D0.8σ 或Kj∑i= Dn0.8 σi≈106～107，其中，σ 为雷达天线主瓣照射区等效RCS；σi为雷达分辨区内等效RCS；D 为雷达距离压缩面积。

例6.13　PtGt为SAR 等效辐射功率，在L 波段，PjGj=80 dBW；β 为星载SAR 天线仰角夹角，β=25°；α 为SAR 在地面投影面方位角夹角，α=40°；H为星载SAR 高度，H=660 km；= 42 dB；Ld为雷达馈线加大气损耗，Ld=0.12；Lj为干扰极化损耗，Lj=0.5；γj为干扰加大气损耗，γj=0.4；Kf为雷达带宽与干扰频谱度之比，Kf=0.6，则=1。

将参数代入式（6.24），得

按照已知的参数，该星载SAR 的干扰有效区域按图6.28 所示配置时，干扰机配在SAR 测像带的中心线上，将参数代入式 （6.20），得r1=dtan α=303 ×tan 40°=254.5 （km）。

将参数代入式（6.18），得d=Htan β=660 ×0.46=306.6 （km）。

如果星载SAR 仰角β 不变，其航线向干扰机方向平移200 km；雷达等效辐射功率和干扰机等效辐射功率不变，求出r2值，如图6.29 所示。

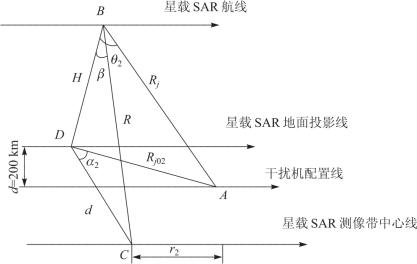
图6.29　星载SAR 向A 方向平移200 km 的示意图

由图6.29 可以看出，Rj缩小，Gt/Gt（θ）增大，式（6.25）可写成

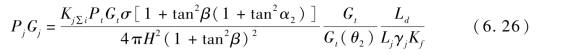
将式（6.25）除以式（6.26），化简得

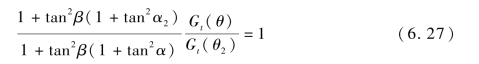
在图6.28 中，取α=40°，Gt（θ）=1，在图6.29 中，Gt（θ2）应为Gt（αi，βi），αi下降，而βi增大，在这个角度，雷达天线的副瓣特性变化缓慢，暂取Gt（θ2）为1.1。

将式（6.27）化简，得

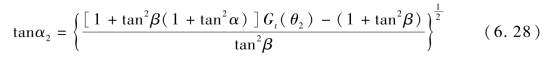
将参数代入式（6.28），得tan α2=1.1。

在图6.29 中，r2=（d-200）tan α2=116 km。

如果星载SAR 仰角β 不变，其航线向远离A 点平移200 km，雷达和干扰机的等效辐射功率均不变，求出r3值，如图6.30 所示。

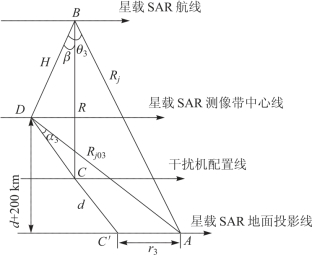
图6.30　星载SAR 向远离A 方向平移200 km 的示意图

由图6.30 可以看出，Rj增大，Gt/Gt（θ）减小，式（6.24）可写成

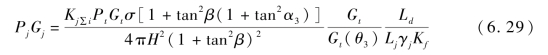
将式（6.24）除以式（6.29），化简得

在图6.28 中，已知α= 40°，Gt（θ）= 1，在图6.30 中，α3＜α。将式（6.30）化简得式（6.31），取Gt（θ3）=0.93，得

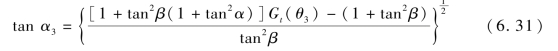
将参数代入式（6.31），得

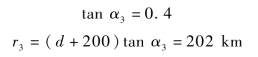
在Gt（θ）中包含了SAR 天线的仰角副瓣和方位角副瓣在变化，对干扰的区域影响较大。在式 （6.26）和式 （6.31）的计算中，对Gt（θ）的取值误差可能很大，因为此刻对天线的副瓣特性没有精确的测量数据。今后要想算得较为准确时，必须对SAR 天线副瓣的方位角和仰角 （Gt（α，β））做精确测量。最好能实际对星载SAR 的有效干扰区通过实测修正一些参数的取值。

根据图6.28、图6.29、图6.30 分析计算，得出r1～r3的数据，可以以干扰站为中心，绘出星载SAR 的干扰有效区和干扰暴露区 （图6.31）。这个星载SAR 工作在L 波段，PtGt= 80 dBW，采用脉冲压缩体制，距地平高度约660 km，计算的干扰机的等效功率为64 dBW。

图6.31　对星载SAR 的干扰有效区和暴露区示意图

A—干扰站位置 （此干扰站有效干扰区域大于10 万平方千米）；虚线区内—干扰有效区；虚线圈外—干扰暴露区（SAR 有效成像区）。

对SAR 能有稳定、可靠的干扰效果，必须确保6个干扰要素：频率瞄得准；干扰天线方向对得准；干扰信号时间连续；有抗变极化抗干扰措施；干扰信号频谱确保覆盖雷达信号频谱；干扰压制系数满足各种不同雷达体制要求。只要这6个干扰要素能满足设计要求，就目前试验结果而言，各种体制的雷达是很难抗掉这种压制式复杂干扰的。而其他欺骗式干扰虽然也能有一定的干扰效果，但是它的针对性较强，要求了解的干扰对象参数较多，并且雷达较为容易抗掉这类欺骗干扰。因此，在设计干扰机时，应以杂波压制式干扰 （满足6个干扰要素的干扰）为主，欺骗干扰为辅。

例如，对SAR 的欺骗干扰或图像欺骗干扰等，它只能在有限的条件下有欺骗干扰。由干扰方程式（6.24）可知

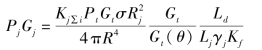
对于星载SAR 而言，它在某一成像带工作时，R 是不变的，而Rj是变化的，雷达接收的目标回波和欺骗干扰信号的时间关系如图6.32 所示。

由图6.32 可知，在SAR 接收机电路中串入“与门”电路，“与门”由距离门信号控制，距离门与目标回波信号同步工作，而欺骗信号很难有机会同步，因此，在“与门”的输出端，绝大多数是目标回波信号输出，而欺骗干扰信号被滤除，使抗干扰得到很好的效果。

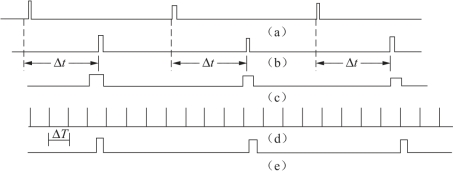
图6.32　雷达同步距离门抗干扰电路示意图

（a）雷达发射基准信号；（b）目标回波信号；（c）雷达距离同步门信号；（d）欺骗干扰信号；（e）雷达输出信号

星载SAR 在目前是应用最广、侦察效果最好的手段之一，在海湾战争和伊拉克战争中，曾发挥过很好的作用。但是，它也有弱点，可以采取适当的干扰措施，可对它进行有效的干扰。一部“地对天干扰机”可使它在10 万平方千米的区域范围内不能进行成像侦察，这是发展中国家对付强权者的一种有效手段之一。

例6.14　在例6.8 的基础上，星载SAR 的β 由25°变成55°，干扰机和雷达的其他参数均没有变化，推算出对此星载SAR 的干扰有效区。

根据式（6.18），得

根据式（6.24），得

已知参数：PjGj=64 dBW，PtGt=80 dBW，Kj∑i=70 dB，β=55°，Gt/Gt（θ）=42 dB，=1。

将式（6.24）改写成

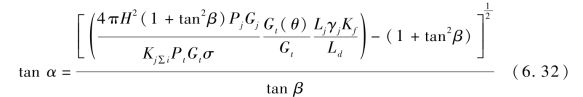
将参数代入式（6.32），得(www.xing528.com)

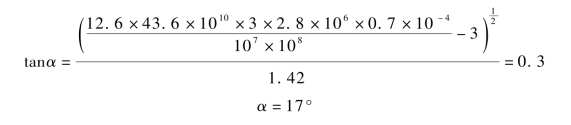
根据式（6.20），得

若星载SAR 航线向干扰机方向平移200 km，将参数代入式（6.28），得

已知的参数：β=55°，α=17°，Gt（θ2）≈1，则

根据式（6.19），得

若星载SAR 航线远离干扰机方向平移200 km，根据式（6.31），得

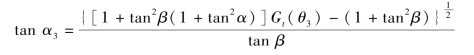
取Gt（θ3）=0.95，β=55°，α=17°，代入式（6.31），得

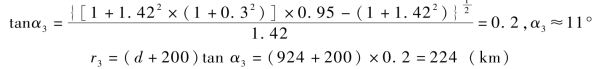
根据r1～r3绘制β=55°时的干扰有效区，如图6.33 所示。

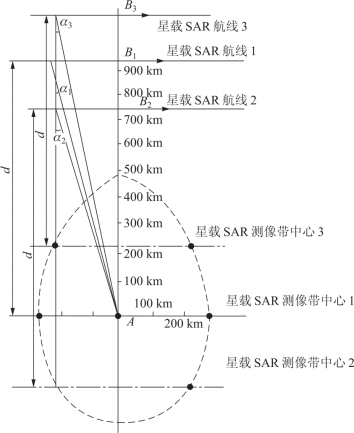
图6.33　在β=55°时的干扰有效区 （其他参数不变）

由图6.31 和图6.32 可以看出，在星载SAR 的仰角β 增大时，雷达干扰机的有效干扰区增大。由此可知，在设计干扰机时，按小的仰角取值，设计出的干扰机可以满足星载SAR 在仰角变化范围内的全部干扰有效区，星载SAR 的仰角变化范围一般在25°～57°内变化。

例6.15　已知星载SAR 参数：H= 660 km，β= 25°，Pt= 5 km，Gt=55 dB，τ/Δτ=40 dB，Kj∑i=32 dB，σ=40 dB，θ0.5=0.3°，σ=40 dB；=0.5，工作在X 波段，α=30°。将参数代入式（6.24），得

按图6.28 配置，干扰机配置在测像带中心线上，将参数代入式（6.20），得

将参数代入式（6.18），得

如果星载SAR 仰角不变，其航线向干扰机方向平移150 km，雷达等效辐射功率和干扰等效辐射功率不变（类似于图6.29 的配置）。

由图6.29 可以看出，Rj缩小，增大。式（6.24）可写成

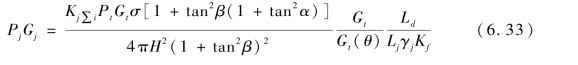
将式（6.24）除以式（6.33），化简得

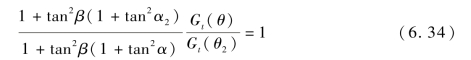
在配置中，此时α=30°，Gt（θ）=1。从这个角度来说，雷达天线副瓣增益变化缓慢，暂取Gt（θ2）=1.1。将式（6.34）化简得

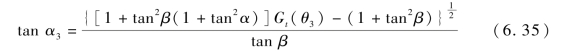
将参数β=25°，α=0.3°，Gt（θ2）=1.1 代入式（6.35），得

如果星载SAR 仰角β 值不变，其航线向远离干扰机方向平移150 km，雷达和干扰机等效辐射功率和其他参数不变，求r3值。

由图6.30 可以看出，Rj缩小，增大。式（6.24）可写成

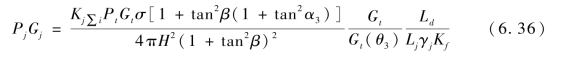
将式（6.24）除以式（6.36），化简得

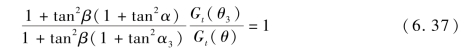
将参数α=30°，Gt（θ）=1，Gt（θ3）=1 代入式（6.37），得

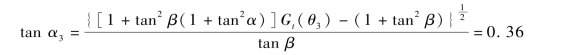
将参数代入式（6.31），得

在Gt（θ）中，SAR 天线的仰角副瓣和方位角副瓣在变化，对干扰的有效区域影响较大。在式（6.35）和式 （6.37）的计算中，对Gt（θ）取值误差较大，因此，计算的对星载SAR 的干扰有效区误差较大，需要在实际测试中不断修正。

根据对X 波段r1～r3的计算数据，可绘出X 波段的地基干扰机对X 波段星载SAR 的有效干扰区，如图6.34 所示。

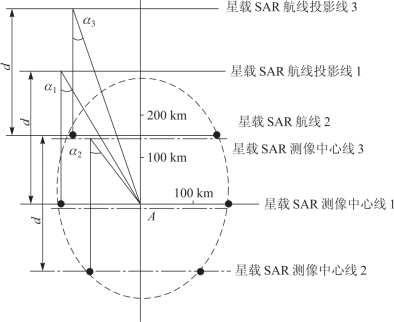
图6.34　星载SAR 在X 波段，β=25°时的干扰有效区

虚线内—干扰有效区；虚线外—干扰暴露区；A—干扰机位置。

例6.16　在X 波段，雷达取β=55°，其他参数同例6.12。

根据式（6.18），得

根据式（6.24），得

若星载SAR 航线向干扰方向平移200 km，将参数代入式（6.28），得

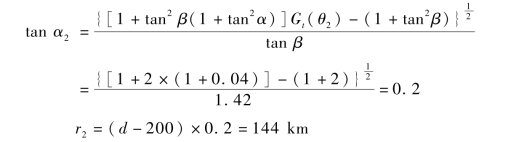
若星载SAR 航线向远离干扰机方向平移200 km，将参数代入式（6.31），得

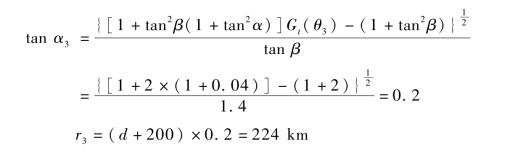
根据r1～r3数据绘制在X 波段、β= 55°时的干扰有效区，如图6.35所示。

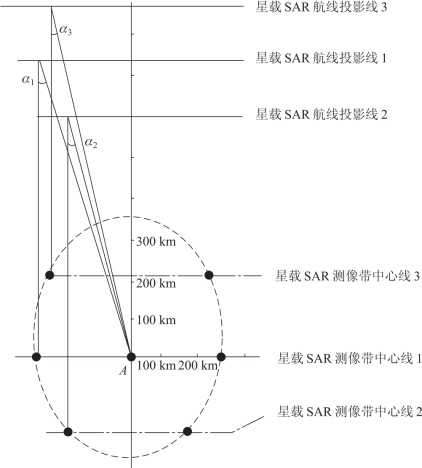
图6.35　X 波段β=55°时的干扰有效区示意图

由图6.35 可以看出，在仰角β 增大时，干扰有效区范围增大。

把图6.31 和图6.33 绘在图6.36 （a）上，把图6.34 和图6.35 绘在图6.36 （b）上，雷达和干扰机参数均相同，但其干扰暴露区有较大差别。

在L 波段的参数：Pt=5 kW，Gt=42 dB，PjGj=64 dBW。

在X 波段的参数：Pt=5 kW，Gt=55 dB，PjGj=74 dBW。

由于雷达天线副瓣特性参数选取不准及其他参数的选取误差，使地对星载SAR 的干扰有效区难以计算准确。在有条件的情况下，最好用实测数据进行校正。

图6.36 为理论计算图。

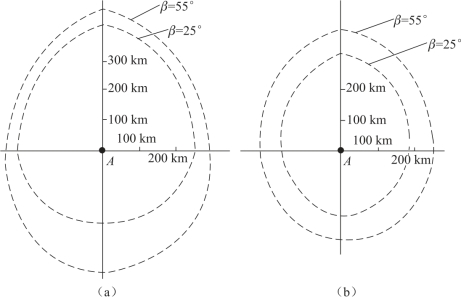
图6.36　在L、X 波段仰角β 不同时干扰有效区的比较

（a）L 波段；（b）X 波段