多项式模运算：11.11.3的解析

前面我们介绍了对任意的环R，可以定义R上的多项式R[x]。当R是有限域时，R[x]自然就是有限域上的多项式。

在GF（p^m）中，令m（x）为一阶数为m在模p下的不可约多项式。若多项式f（x）∈GF（p^m），则f（x）可表示为下列阶数为m-1或更小的多项式。

其中，系数a_i为模p的整数；f（x）为模m（x）后的余数多项式。

1.GF（p^m）中的模加法运算

令多项式f（x）、g（x）∈GF（p^m），且

加法运算为：

其中，r_i≡（a_i+b_i）mod p，0≤i≤m-1

【例11-41】 在GF（3³）中，若f（x）=x²+x+2，g（x）=x²+2x+2，m（x）=x³+2x+1，则

f（x）+g（x）=x²+x+2+x²+2x+2≡2x²+1（mod（x³+2x+1））

2.GF（p^m）中的模乘法运算(www.xing528.com)

令多项式f（x）、g（x）∈GF（p^m），且

乘法运算为：

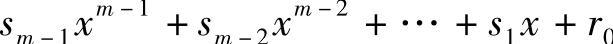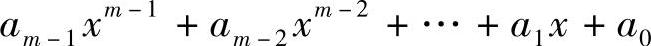其中，多项式是多项式与多项式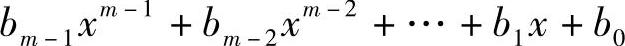相乘再模m（x）后的余数多项式。

【例11-42】 （1）证明m（x）=x⁸+x⁴+x³+x+1是GF（2⁸）中的不可约多项式。

（2）考虑GF（2⁸）中的多项式f（x）=x⁶+x⁴+x²+x+1和g（x）=x⁷+x+1，计算在模m（x）下的f（x）+g（x）和f（x）·g（x）。

【解析】 （1）由于GF（2⁸）中的所有次数≤8/2=4的不可约多项式为x，x+1，x²+x+1，x³+x+1，x³+x²+1，x⁴+x+1，x⁴+x³+1，计算

可知f（x）不能被次数≤4的不可约多项式整除，即m（x）=x⁸+x⁴+x³+x+1是GF（2⁸）中的不可约多项式。

（2）在模m（x）下计算