多项式环介绍与应用

对于整环R上全体多项式组成的集合R[x]，设多项式

且f（x）、g（x）∈R[x]。

在R[x]上定义的加法为

R[x]对于该加法构成了一个交换加法环。

零元素即零多项式为0，任意多项式f（x）的加法逆元为：

设多项式

且f（x）、g（x）∈R[x]。

在R[x]上定义的乘法为

其中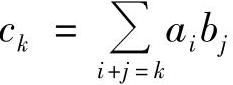，，0≤k≤n+m，即

R[x]对于该乘法满足结合律和交换律，且有分配律。

定义11.22 设f（x）、g（x）是整环R上的任意两个多项式，其中g（x）≠0，如果存在多

项式q（x）使得等式

f（x）=g（x）·q（x）

成立，则称g（x）整除f（x），记作(www.xing528.com)

g（x）|f（x）

g（x）叫做f（x）的因式；f（x）叫做g（x）的倍式。

【例11-38】 整系数多项式环Z[x]中

（3x+5）|（3x²+5x）（x²+1）|（x⁴-1）

定义11.23 设f（x）是整环R上的非常数多项式，如果它除了因式1和f（x）外，没有其他因式，

那么f（x）叫做不可约多项式；否则f（x）叫做可约多项式或合式。

定义11.24 设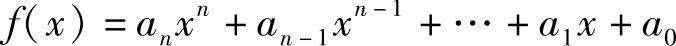，a_n≠0，则称多项式f（x）的次数为n，记为deg（f（x））=n。

【例11-39】 在Z[x]中

3x+5的次数为1

x²+5x+7的次数为2

x⁸+x⁴+x³+x+1的次数为8

定理11.20对于整环R上的两个多项式f（x）和g（x），一定存在多项式q（x）和r（x）也在整环R上，使得

f（x）=q（x）·g（x）+r（x）其中，deg（r（x））≤deg（q（x））。此定理也称为多项式欧几里得除法。