如何求乘法逆元：欧几里得算法

定义11.6 对于整数a和正整数n，当gcd（a，n）=1时存在整数c，使得

ac≡1（mod n）称c为a关于模n的乘法逆元，记为a^-1。

根据互素的性质4），存在整数s和t，使得as+nt=1，而nt≡0（mod n），所以只需取c=s即可。同样地，如果a也是正整数，则t是n关于模a的乘法逆元。

乘法逆元并不唯一，如只要ac≡1（mod n）成立，则对任意的整数h，也有a（c+nh）≡1（mod n），即c+nh也是a的模n乘法逆元。但是在模n意义下，是唯一的。

定理11.9 如果gcd（a，n）=1，n为正整数，则a的所有模n乘法逆元都是模n同余的。

设c₁和c₂都是a的模n乘法逆元，即ac₁≡1（mod n），ac₂≡1（mod n），从而a（c₁-c₂）≡0（mod n），因为gcd（a，n）=1，所以n|（c₁-c₂），c₁和c₂关于模n同余。

根据前面的分析知，对于互素的两个数a和n，要求a关于模n的乘法逆元，只需要求出表达式as+nt=1的一组解（s，t）即可。

根据欧几里得算法可得

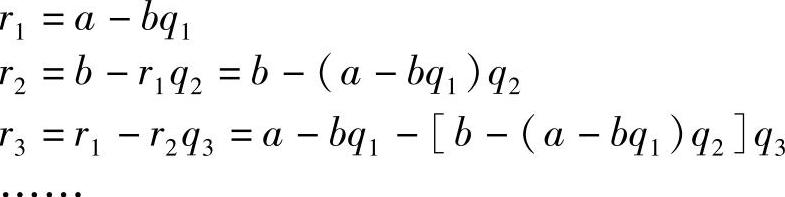
最后得到r_n关于a和b的线性组合表达式，如果r_n=1，a和b都为正整数，则组合表达式中a和b的系数对应各自关于对方的乘法逆元；如果r_n≠1，r_n+1=0，则r_n为a和b的最大公因子。

扩展的欧几里得算法为此方法的实现，其确定两个正整数的最大公约数或者互素的两个正整数的各自的乘法逆元。其算法描述如下：

Extended EUCLID（a，b且a＞0，b＞0）

1）（X₁，X₂，X₃）←（1，0，b）；（Y₁，Y₂，Y₃）←（0，1，a）(www.xing528.com)

2）如果Y₃=0返回X₃=gcd（a，b）；无逆元

3）如果Y₃=1返回Y₃=gcd（a，b）；Y₂=a^-1（mod b）

4）q=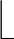X₃/Y₃」

5）

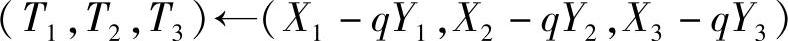
6）（X₁，X₂，X₃）←（Y₁，Y₂，Y₃）

7）（Y₁，Y₂，Y₃）←（T₁，T₂，T₃）

8）回到2）

其中的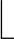X₃/Y₃」表示不大于X₃/Y₃的最大正整数。

【例11-17】 用扩展的欧几里得算法求550^-1mod 1769。

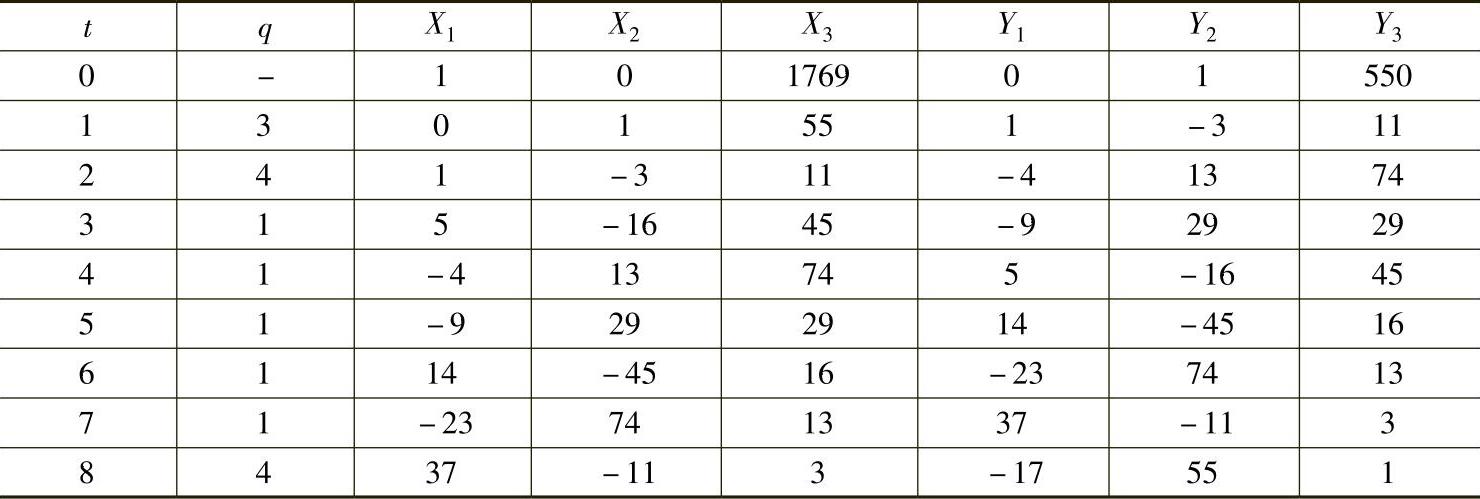
【解析】 求550^-1mod 1769的算法过程如表11-1所示，其中t为算法循环次数。当t=7时，Y₃=1，此时，Y₂=550，即550^-1（mod 1769）≡550。

表11-1 求550^-1mod 1769的算法过程