素数检测方法与原理：Miller-Rabin测试及其应用

素数有无限多个，但目前还没有一个规律能确定所有的素数。有一些检测不太大的整数为素数的方法和对于大的整数的近似检测算法。

定理11.1 如果整数a＞1，则a的大于1的最小因子一定是素数。

因为如果最小因子q是合数，那么它有大于1的因子q₁，而q₁显然也为整数a的因子且小于q，这与q是最小因子相矛盾。

推论11.1 合数a的大于1的最小因子不超过。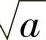

定理11.2 设n是一个大于1的正整数，如果对所有小于或等于n的素数p，都有p⫮n，则n一定是素数。

1.Eratosthenes筛选法

下面介绍求不超过一个正整数n的全部素数的有效方法——古老的Eratosthenes筛选法。该方法是古希腊数学家Eratosthenes发明的，其原理建立在定理11.2之上。现用n=100这个具体的例子来介绍Eratosthenes筛选法。

【例11-3】 求出所有不超过100的素数。

【解析】 因为，小于或等于10的素数有2，3，5，7，则可以按如下算法求出所有不超过100的素数。

1）输出2，3，5，7，i=8；

2）如果2|i，则i不是素数，转到7）；

3）如果3|i，则i不是素数，转到7）；

4）如果5|i，则i不是素数，转到7）；

5）如果7|i，则i不是素数，转到7）；

6）输出i的值；

7）i=i+1；

8）如果i＞100，程序结束；

9）否则返回到2）。

输出的结果为

2，3，5，7，11，13，17，19，23，29，31，37，41，43，47，53，59，61，67，71，73，79，83，89，97

对于一般n，Eratosthenes筛选法可表述如下：(www.xing528.com)

1）找出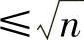的全部素数p₁，p₂，…，p_m；

2）在1～n中分别划去p₁，p₂，…，p_m的全部倍数（本身除外）；

在2）步完成后剩下的数除1外就是不超过n的全部素数。

2.费马（Fermat）定理检测法

根据费马定理可以对大的正整数近似检测其素性。费马定理给出了整数n为素数的必要条件：

对任意的整数a，如果满足gcd（a，n）=1，则a^n-1≡1（mod n）。

也就是说，如果存在与n互素的整数a，不满足a^n-1≡1（mod n），则说明n肯定不是素数。

反之，如果有整数a，满足条件gcd（a，n）=1且a^n-1≡1（mod n），则n不一定为素数，此时称n是关于基数a的伪素数。

【例11-4】341，561，645，1105等都满足

2^n-1≡1（mod n）

但它们都是合数，是基数为2的伪素数。

即使对于所有与n互素的整数a都满足a^n-1≡1（mod n），n也不一定为素数。不过相比较而言，满足以上必要条件的数有较大概率为素数，因此，可以应用以上必要条件来近似检测素数，通过随机选择多个a（一般取1≤a≤n-1）进行测试，可以将误差限定在一定范围之内。

3.Miller-Rabin概率测试法

素数还具有更强的性质：设n是一个大于4的奇素数，n-1=2^s×r，s和t是正整数，r为奇数，则对所有满足gcd（a，n）=1的整数a，下面两个条件中至少有一个被满足：

1）a^r≡1（mod n）；2）对于某个j，0≤j≤s-1，有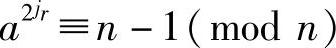或a^2jr≡-1（mod n）。

则称n通过以a为基的Miller-Rabin概率测试。

等价地，这两个条件都不满足的奇整数肯定为合数；而满足这两个条件之一的奇数可能是素数，也可能是合数，这样的合数被称为强伪素数。根据此性质，可以将素数检测的误差进一步降低。基于此性质，Miller-Rabin概率测试得到广泛应用。

定理11.3 若n是素数，a是整数，且n不能除尽a，则n必然通过以a为基的Miller-Rabin测试。

从该定理可验证，Miller-Rabin测试若能通过，费马定理便可满足。