混沌密码：基本原理解析

最早将混沌系统应用于密码学的思想可以追溯到1949年香农（Shannon）出版的经典文章“Communication Theory of Security System”。自20世纪80年代以来，应用混沌系统构造新型密码系统的想法得到了越来越多的关注，这一想法来源于混沌系统和密码学系统之间的自然联系：强混沌系统的动力学特性大致对应着高强度密码学系统的某些安全特征，而具有良好混合性的传统密码系统又暗含着拟混沌现象。

混沌的许多基本特征：对初始值的敏感性；产生伪随机的却又是确定可再生的序列；混沌轨道的极不规则性以及系统局部扩展、压缩、折叠，使得混沌系统的输出表现出类随机性；指数发散性，如平面上任意接近的两点随着迭代的进行会呈指数性发散等。这些都和“混淆”、“扩散”等密码学特性相联系，也就是说，混沌系统具有密码学特性。

另一方面，传统的密码系统都是由确定的加密过程产生的伪随机序列，即密码系统具有类混沌特性。混沌系统与密码学的关系如表10-2。目前，混沌密码主要有两个研究方向：

●以混沌同步技术为核心的混沌保密通信系统，主要基于模拟混沌电路系统；

●利用混沌系统构造新的流密码和分组密码，主要基于计算机有限精度下实现的数字化混沌系统。

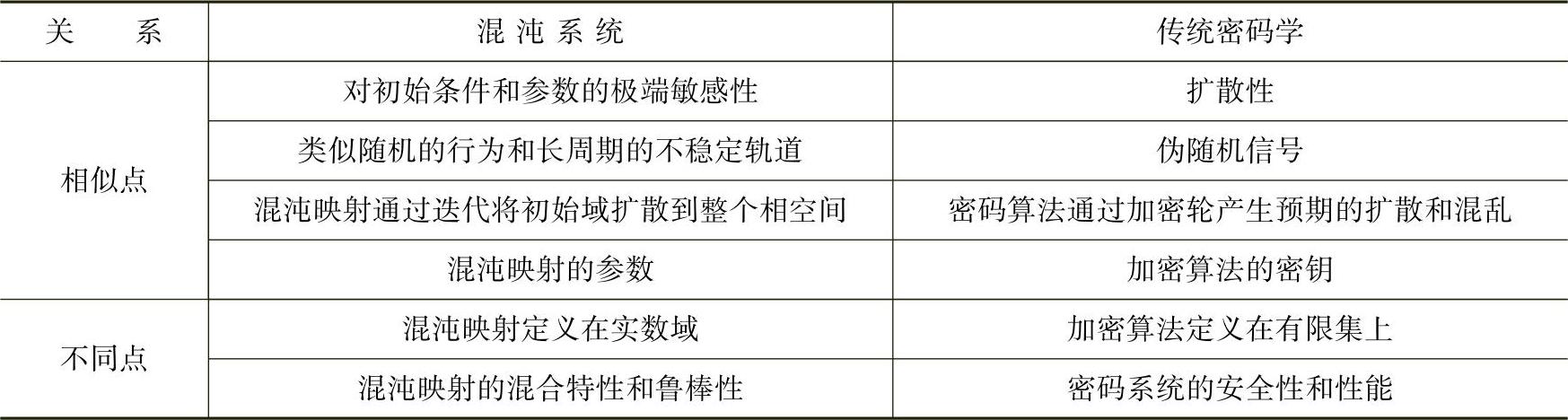
表10-2 混沌系统与密码学的关系

(www.xing528.com)

关于如何选取满足密码学特性要求的混沌映射是一个需要解决的关键问题。L.Kovarev在其文献中给出了这方面的一些指导性建议。选取的混沌映射应该至少具有如下三个特性：混合特性（Mixing Property）、鲁棒混沌（Robust Chaos）和具有大的参数集（Large Parameter set）。

1）混沌特性：将明文看做初始条件域，则混合属性是指将单个明文符号的影响扩散到许多密文符号中去。显然，该属性对应密码学中的扩散属性。具有混合属性的系统具有较好的统计特性，当迭代次数n→∞时，密文的统计性质不依赖于明文的统计性质，从而由密文的统计结构不能得到明文的结构。

2）鲁棒混沌：鲁棒混沌是指在小的参数扰动下，系统仍保持混沌状态。但是一般来讲，大多数混沌吸引子不是结构稳定的，而非鲁棒混沌的系统具有弱密钥。

3）大的参数集：密码系统安全性的一个重要的衡量指标是Shannon熵，即密钥空间的测度，在离散系统中常用log₂K近似，其中K为密钥的数目。因而，动力系统的参数空间越大，离散系统中反应的K就越大。

需要指出的是具有上述属性的系统不一定安全，但不具备上述属性所得到的混沌加密系统必然是弱的保密系统。所以，选择混沌系统时，我们应该考虑在大的参数集中具有鲁棒混沌混合属性的系统。