Okamoto身份识别方案优化

Okamoto协议是Schnorr协议的改进，在假设计算中的一个特定的离散对数是难解的条件下，能够证明这个方案是安全的。

1.选择参数

Okamoto识别方案同样需要一个可信任的验证中心TA，且选择参数如下：

●p、q是两个大素数，且q|（p-1）。

●α₁、α₂∈Z_p^*，都为q阶元，且计算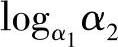是困难的。

●h（x）是输出为t bit的单向函数，t是一个安全参数。

●选择签名生成算法Sig_ta和签名验证算法Ver_ta。

2.TA向示证者P颁发证书

1）TA为P建立身份信息，并颁发一个身份识别串ID_P。

2）P选取随机数x₁和x₂作为自己的私钥，x₁、x₂∈[1，q-1]，计算出公钥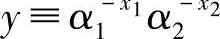（mod p），P到TA处注册其公钥。

3）TA计算签名S=Sig_ta（ID_P，y），将身份证书Cert_P=（ID_P，y，S）发送给P。

3.示证者P向验证者V证明自己的身份(www.xing528.com)

1）P选择随机数r₁和r₂，且r₁、r₂∈[1，q-1]，计算

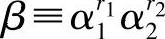（mod p）。

2）P发送自己的身份证书Cert_P和β给V。

3）V通过检查证书Cert_P来验证TA的签名。

4）V任选取一整数e∈[1，2^t]作为询问值发送给P。

5）P计算w₁≡r₁+x₁e（mod q），w₂≡r₂+x₂e（mod q）把w₁、w₂作为对V的应答值发送给V。

6）V验证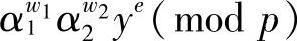，判断其是否等于β，若相等，则V相信对方就是P。

实际上，若双方都诚实，则

4.安全性分析

类似Schnorr识别协议的分析，Okamoto识别协议的完全性和合理性的证明是直接的。虽然Okamoto协议在速度和效率上都不如Schnorr协议，但假设计算离散对数log_α1α₂是难题，可以证明Okamoto协议是安全的。

安全性证明的思想为：假设示证者P通过执行该协议多项式次来向验证者V证实自己的身份，验证者V能得到有关P的秘密随机数x₁和x₂的一些信息。如果是这样，那么可以证明P和验证者V联合起来有很高的概率能在多项式时间内计算出离散对数log_α1α₂，这与开始的假设相矛盾，因此证明了验证者V通过参与该协议多项式次必定不能得到有关P的秘密随机数x₁和x₂的任何信息。