完整解析Diffie-Hellman密钥协商方案

Diffie-Hellman密钥协商方案是W.Diffie和M.Hellman于1976年提出的，该方案实质上是一个通信双方进行密钥商定的协议，它的安全性基于有限域上计算离散对数的困难性。Diffie-Hellman密钥协商方案本身不能用于加/解密，设计的目的在于使通信双方能够安全地交换密钥，得到一个共享的会话密钥。

1.协商方案描述

设p是大素数，g是模p的本原元素，p和g公开。用户A为了和用户B进行保密通信，他们必须获得一个共享的密钥，采用Diffie-Hellman密钥协商方案获取共享密钥的协商过程如下：

1）用户A随机选择一个私有的大整数x_A＜p，计算公钥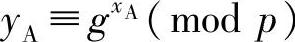，并将结果传送给用户B。

2）用户B随机选择一个私有的大整数x_B＜p，计算公钥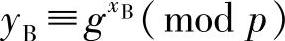，并将结果传送给用户A。

3）用户A计算。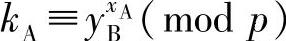

4）用户B计算。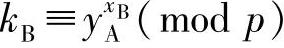

用户A和B计算出的k_A、k_B就是共享的会话密钥k，这是因为

【例7-1】 假设Diffie-Hellman密钥协商方案使用的素数p=97，p的一个本原元素为g=5。通信双方A和B分别选择秘密随机数x_A=36和x_B=58。试问：共享的会话密钥k是多少？

【解析】 用户A和B分别计算出各自的公钥：

通信双方交换公钥，然后各自独立地计算出共享的会话密钥k为：

可见：k_A=k_B=k。(www.xing528.com)

协商过程完成，用户A和B获得了完全一样的会话密钥k。而攻击者最多能够知道p=97，g=5，y_A=50，y_B=44，要想得到会话密钥k，则必须得到x_A、x_B中的一个，这意味着需要求离散对数。因此攻击者计算出k=75是很不容易的。

2.安全性分析

尽管Diffie-Hellman密钥协商方案的安全性基于有限域上计算离散对数的困难性，且方案简单易行，但它很容易遭受中间人攻击，攻击方法如下：

1）在用户A将他的公钥y_A发送给B的过程中，中间人M（即攻击者）截取y_A，并用自己的公钥y_M取代y_A发送给用户B。

2）在用户B将他的公钥y_B发送给A的过程中，中间人M截取y_B，并用自己的公钥y_M取代y_B发送给A。

3）A、B和M三者分别计算会话密钥，计算的结果如下：

A与M共享会话密钥k_A：

B与M共享会话密钥k_B：

一般情况下k_A≠k_B，但A与B对此一无所知。

4）接下来，在A与B通信过程中，A用会话密钥k_A加密他发送的消息，B则用会话密钥k_B加密他发送的消息。中间人M可以设法截取来自A的消息并用k_A解密，再用k_B重新加密后发送给B；对于来自B的消息则先用k_B解密，然后再用k_A加密后发送给A。这样，中间人M就可以轻易监视A与B的通信，甚至还能够在其中实施篡改、伪造或假冒攻击。