不可否认的签名方案的介绍

不可否认的签名最主要的一个特点是如果没有签名者的合作，签名的有效性就得不到验证。只要签名者参与了验证，那么签名者既不能使验证者接受一个无效的签名，也不能使验证者相信一个有效签名是无效的。这就防止了由签名者签署的消息在没有经过他本人同意而被复制和分发的可能性。一旦接收者对签名的验证通过，签名者就没有理由否认。不可否认的签名是由Chaum和van Antwerpen在1989年提出来的。其具体方案描述如下。

1.不可否认的签名方案

（1）初始化参数定义

●p是大素数，在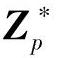中离散对数是难解的；

●q也是大素数，且p=2q+1；

●α是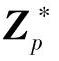中的一个阶为q的元素，1≤α≤q-1；

●G表示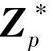上阶为q的乘法子群。

令β≡α^x（mod p）

其中，p、α、β是公钥；x是私钥。

（2）签名过程

A拥有私钥x，欲对消息m签名，m∈G，则可计算

s=Sig_x（m）≡m^x（mod p）得到的签名s∈G。

（3）验证过程

1）B欲验证签名，可随机选取参数e₁、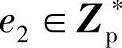，计算

将结果c发送给A。

2）A计算

d≡c^x-1（mod q）（mod p）将计算结果d发送给B。

3）B接收d并验证

d≡m^e1α^e2（mod p）

如果成立，便有充分的理由认为s是A对m的有效签名。证明如下：(www.xing528.com)

因为

所以

（4）否认协议

1）B收到签名后，随机选取参数e₁、，计算

c≡s^e1β^e2（mod p）将结果c发送给A。

2）A计算

将计算结果d发送给B。

3）B接收d并验证，发现

4）B随机选取参数f₁、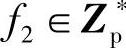，计算

将计算结果c′发送给A。

5）A计算

将计算结果d′发送给B。

6）B计算

当且仅当

B认为签名s是伪造的。

2.不可否认签名的安全性

1）B是验证了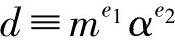（mod p）后，才同意接收s作为m的签名的，则可以推知s≠m^x（mod p）的情况下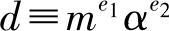，（mod p）的概率只有1/q，因此一个伪造的签名能使B相信的概率只有1/q。

2）若s≡m^x（mod p）且B遵守否认协议，又存在d和d′使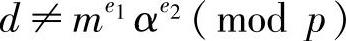，d′≠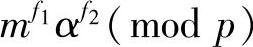，则可以推知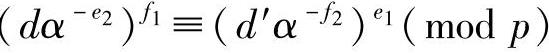成立的概率为1/q。

从上面的安全性分析得知，如果A想用其他d值来否认s是他的签名，能成功的概率只有1/q。只要q充分大，B就没有理由否认自己的签名。