生日攻击：40位消息摘要存在高碰撞率

1.生日问题

生日攻击来自于概率论中的生日问题：在一个教室中至少要有k个学生才能够使得有两个学生生日相同的概率大于1/2，求k值至少多大。

定义概率P（n，k）：设有k个整数项，每一项都在1到n之间等可能地取值，则k个整数项中至少有两个取值相同的概率为P（n，k）。生日问题就是求使得P（365，k）≥0.5的最小k。

定义概率Q（365，k）：考虑k个数据项中任意两个取值都不同的概率，记为Q（365，k）。如果k＞365，则不可能使得任意两个数据都不相同，因此假定k≤365。

k个数据项中任意两个都不相同的所有取值方法数为

即第1个数据项可从365个中任取一个，第2个数据项可在剩余的364个中任取一个，依此类推，最后一个数据项可从365-k+1个值中任取一个。

如果去掉任意两个都不相同这一限制条件，可得k个数据项中可以取值相同的所有取值方法数为365^k，则k个数据项中任意两个取值都不同的概率为

而k个数据项中至少有两个取值相同的概率为

当k=23时，P（365，23）=0.5073，即只要教室中学生的人数大于23人，班上有两个人生日相同的概率就将大于1/2。若k取100，则P（365，100）=0.9999997，即获得如此大的概率。当人数k给定时，得到的至少有两个人的生日相同的概率比想象的要大得多，所以称这一问题是生日悖论。

2.寻找具有相同输出摘要的碰撞消息

将生日问题推广，得到一种生日攻击方法：寻找Hash函数具有相同输出摘要的两个任意输入消息。已知Hash函数有n个可能的输出摘要，特别地，如果输出摘要为m bit长，即可能的输出摘要个数n=2^m，若Hash函数的k个随机输入消息中至少有两个产生相同输出的概率大于1/2，求k值至少多大。

因为Hash函数有n个可能的输出摘要，根据生日问题可知，k个随机输入消息中至少有两个产生相同输出的概率为：

取P（n，k）=1/2(www.xing528.com)

则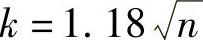

当输出摘要为m bit长，可能的输出摘要个数n=2^m时，

3.已知特定的输出摘要寻找碰撞消息

已知Hash函数有n个可能的输出摘要，H（x）是一个特定的输出摘要，如果对Hash函数随机取k个输入消息，则至少有一个输入消息x′使得H（x′）=H（x）的概率为0.5时，求k值至少多大。

因为Hash函数有n个可能的输出摘要，所以输入消息x′产生的输出摘要H（x′）等于特定输出摘要H（x）的概率是1/n；反过来说，H（x′）≠H（x）的概率是1-1/n。

如果x′取k个随机值，而Hash函数的k个输出摘要中没有一个等于H（x），其概率等于[1-1/n]^k，那么x′取k个随机值得到函数的k个输出摘要中至少有一个等于H（x）的概率为1-[1-1/n]^k。

由（1+a）k≈1+ka，其中a＜＜1，可得

1-[1-1/n]^k≈1-[1-k/n]=k/n

若使上述概率等于0.5，则k=n/2。

特别地，如果Hash函数的输出摘要为m bit长，即可能的输出摘要个数n=2^m，则Hash函数随机取k个输入消息，至少有一个输入消息x′使得H（x′）=H（x）的概率为0.5，此时k=2^m-1。

生日攻击意味着要保证消息摘要对碰撞问题是安全的，消息摘要的长度应该有一个下界。例如，长度为40bit的消息摘要是非常不安全的，因为仅仅在2²⁰个随机Hash函数值中就有50%的概率发现一个碰撞。所以对于安全的消息摘要，现在实际使用的消息摘要一般为160bit或者更长。