有限域上的椭圆曲线简介

1.定义

椭圆曲线主要有实数域上的椭圆曲线、有限域GF（p）上的椭圆曲线和有限域GF（2^m）上的椭圆曲线，不同数域上的椭圆曲线的表示形式不一样，甚至在其上的运算也不一样。对于椭圆曲线上的密码体制，最为常用的是由方程

y²≡x³+ax+b（mod p）

所定义的有限域GF（p）上的椭圆曲线，其中非负整数a和b满足a、b∈GF（p），p为素数，且有4a³+27b²≠0（mod p）。该椭圆曲线上只有有限个点N，其范围由Hasse定理确定。

Hasse定理：如果E_p（a，b）是定义在GF（p）上的椭圆曲线，N是E_p（a，b）上的点（x，y）∈GF（p）的个数，则。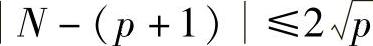

【例5-16】 GF（11）上的一个椭圆曲线E₁₁（1，0）：y²≡x³+x（mod 11）（即a=1，b=0），则满足该椭圆曲线在GF（11）上的解为（即该椭圆曲线上的点）：

（0，0）、（5，3）、（5，8）、（7，3）、（7，8）、（8，5）、（8，6）、（9，10）、（9，1）、（10，3）、（10，64）和无穷远点O。

该GF（11）上的椭圆曲线上共有12个点（包括无穷远点O）。除了（0，0）点以外，对应于每一个x值，均有两个点，如（5，3）和（5，8），而且它们是关于y=5.5对称的（即5.5=11/2）。

2.加法运算

设E是椭圆曲线，曲线示意图如图5-4所示，P、Q是曲线上的两个点，连接P、Q两点的直线与曲线相交于第三个交点R，O是无穷远点，椭圆曲线E上的加法运算定义如下。

1）O+O=O

2）对于曲线上的所有点P满足：P+O=P

3）若点R和S位于一条垂线上（x坐标相同），则点R与S互逆，满足：R+S=O，即S=-R

4）对于所有点P与Q，满足加法交换律，即P+Q=Q+P

5）对于所有点P，Q和R，满足加法结合律，即P+（Q+R）=（P+Q）+R

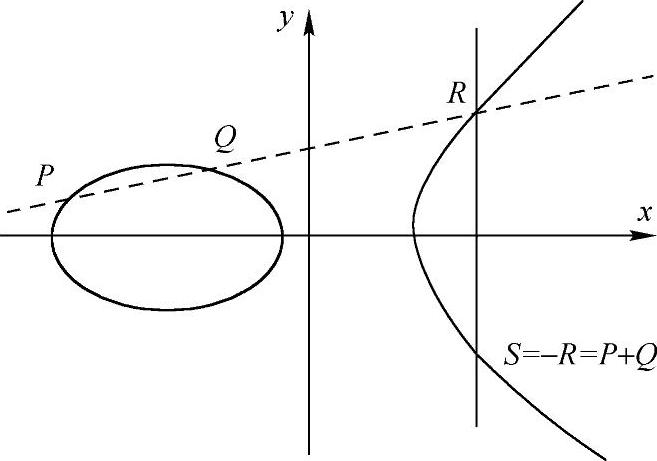
图5-4 椭圆曲线E示意图

6）设l是连接P、Q的直线，R是直线l与曲线E的第三个交点，

①如果P与Q是两个不同且不互逆的点，则有

P+Q+R=O，即P+Q=-R

②如果P=Q，则l成为切线，则有2P=P+P=-R(www.xing528.com)

类似有，3P=P+P+P，kP=P+P+P+…+P（等式右端k个P相加）

另外：若存在最小的正整数n，使得nP=O，其中O是无穷远点，则称n是P点的阶。

可以证明，只要非负整数a和b满足：4a²+27b²（mod p）≠0，那么E_p（a，b）表示模p的椭圆群，这个群中的元素（x，y）和无穷远点O共同组成椭圆群，这是一个阿贝尔群，即对于椭圆曲线上的任意两个点：P（x₁，y₁）和Q（x₂，y₂），存在第三个点S（x₃，y₃）=P+Q也在椭圆曲线上。此时有限域上椭圆曲线上的加法运算规则为

其中，

【例5-17】 考虑椭圆曲线E₂₃（1，1）：y²≡x³+x+1（mod 23），设P=（3，10），Q=（9，7），且P、Q∈E₂₃（1，1），求-P、P+Q、2P。

【解析】 设椭圆曲线E_p（a，b）上所定义的点集为{（x，y）0≤x＜p，0≤y＜p，且x、y均为整数}和无穷远点O。则本例中椭圆曲线E₂₃（1，1）上的点集如表5-3所示，表中未给出O。

表5-3 E₂₃（1，1）上的点集

1） P=（3，10）∈E₂₃（1，1）

则 -P=（3，-10）

又 -10（mod 23）≡13

所以-P=（3，13），也在E₂₃（1，1）上。

2）P（x₁，y₁）=（3，10），Q（x₂，y₂）=（9，7），P、Q∈E₂₃（1，1）

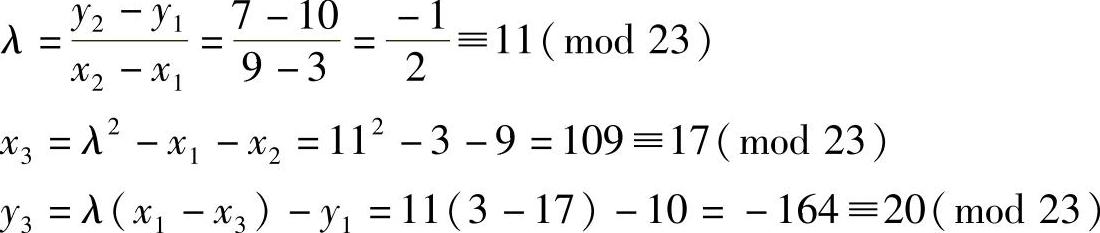
所以P+Q=（17，20），也在E₂₃（1，1）上。

3）P（x₁，y₁）=（3，10），此时a=1，b=1。若求2P，则

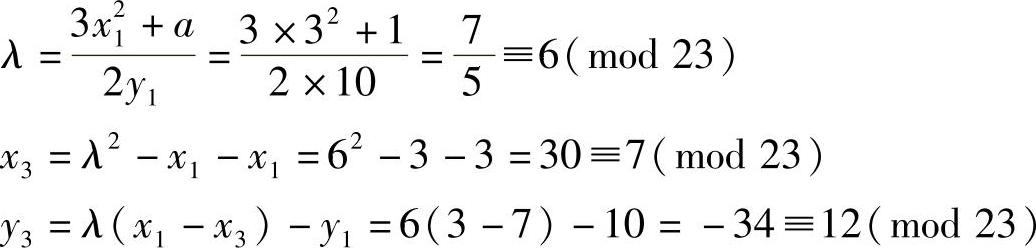
所以2P=（7，12），仍然在E₂₃（1，1）上。