ElGamal算法：加密、解密的描述

1.相关数学基础

（1）有限域的基本理论

有限域中元素的个数称为域的阶。每个有限域的阶必为素数的幂。

对任意的素数p和正整数n，存在pⁿ阶域，记为GF（pⁿ）。当n=1时，GF（p）也称为素数域。

对于素数p，整数集合{0，1，2，…，p-1}按通常的四则代数运算在模p意义下构成一个有限域GF（p）。其中的运算为：

加法：任意a，b∈GF（p），有a+b≡r（mod p），r∈GF（p）。

乘法：任意a，b∈GF（p），有a·b≡s（mod p），s∈GF（p）。

如两个元素0，1构成二元域GF（2）。其中的加法和乘法运算为

加法运算：1+0=0+1≡1（mod 2），1+1≡0（mod 2），0+0≡0（mod 2），即为逻辑异或运算。

乘法运算：1·0=0·1≡0（mod 2），1·1≡1（mod 2），0·0≡0（mod 2）

（2）本原元素

令GF^*（p）为GF（p）中所有非零元素的集合，即GF^*（p）={1，2，…，p-1}。可以证明，在GF^*（p）中至少存在一个元素g，使得GF^*（p）中任意非零元素可以表示成g的某次方幂。g称为GF（p）的本原元素（或生成元）。

【例5-12】 有限域GF（23）中，5ⁱ（mod 23）（i=0，1，…，22）值的范围为{1，2，…，22}，所以5是GF（23）的本原元素，见表5-1。

表5-1 5ⁱ（mod23）的全部整数值

2.ElGamal算法的加密和解密

（1）参数定义和密钥生成

选取大素数p，g∈Z_p*是一个本原元素（生成元）。p、g为系统中所有用户共享。系统中每个用户U都随机挑选一个整数x_U，1≤x_U≤p-1并计算：

用户U的公钥为（y_U，p，g），私钥为x_U。

（2）加密算法

假设某一用户A想把明文M发送给用户B，用户A执行下面几步来加密消息M：

1）用户A将明文M进行编码为一个在0到p-1之间的整数m作为传输的明文；

2）用户A挑选一个秘密随机数r（2≤r≤p-2）并计算；

c₁≡g^r（mod p），c₂≡m·y^r_B（mod p）得到密文组（c₁，c₂），其中y_B是用户B的公钥；

3）用户A把密文组（c₁，c₂）传送给用户B。

（3）解密算法(www.xing528.com)

用户B接收到密文二元组（c₁，c₂）后，计算：

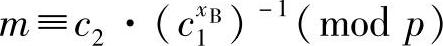
进行解密，明文消息m被恢复，其中x_B是用户B的私钥。

由于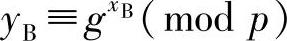

所以

【例5-13】 选取素数p=19，本原元素g=13，假设用户B选择整数x_B=10作为私钥，计算用户B的公钥y_B：

用户B将y_B公开，而将x_B=10保密。

假设用户A想秘密地发送编码为m=11的明文给B，用户A执行如下加密过程：

用户A选择一个随机数，假设r=8，并计算：

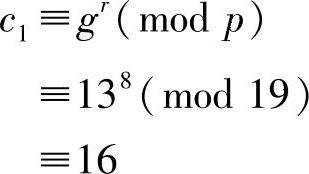
同时，A还计算：

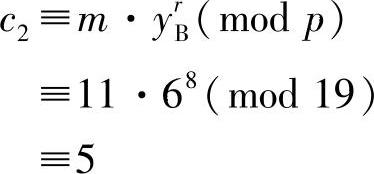
最后，用户A把密文二元组（16，5）发送给用户B，用户B收到后计算：

还原出明文m。

【例5-14】 在ElGamal加密体制中，设素数p=11，本原元素g=7，发送方A选择随机整数r向接收方B发送信息，使得明文m=20加密后的密文是c=（5，c₂），已知接收方B的公开钥是y_B=3，求c₂。

【解析】 已知 g=7，p=11

根据 c₁≡g^r（mod p）

计算

5≡7^r（mod 11）

r≡2

再根据 c₂≡m·y^r_B（mod p）

求得

c₂≡20·3²（mod 11）≡4（mod 11）