参数选择对安全性的影响

1.模数n的选择

（1）不同用户不能共享模数n

对于给定的模数n，满足e_id_i≡1（mod n）的加/解密密钥对（e_i，d_i）很多，因此有人建议在通信中用同一个参数n以节约存储空间，但可证明这对于系统来说是有安全隐患的。

假设密钥对（e_i，d_i），（e_j，d_j）是同一参数n的两个不同参数对，当gcd（e_i，e_j）=1时，对于同一明文m分别加密得密文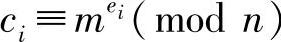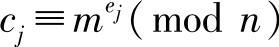，。由欧几里得算法知，必定存在整数t和s，满足te_i+se_j=1，因此有。

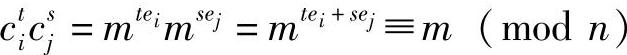（2）n要足够大

如果模数n不够大，则n很容易被分解。破译者一旦能将n分解成p和q之积，就易求得φ（n）=（p-1）（q-1），于是解密密钥d就可以由扩展欧几里得算法求出。

2002年，Atkins，Graff，Lenstra和Lerland利用多重二次数域筛选法成功分解了158位十进制数。目前因子分解的能力对154位十进制数（512bit）的模数已经造成威胁，估计在未来一段比较长的时期，使用介于1024bit至2048bit之间的模数n是安全的。

2.p和q的选择

（1）p和q应为强素数

定义：任一素数p，若满足下列条件，则称之为强素数或一级素数。

●存在两个大素数p₁及p₂，使得p₁|p-1，p₂|p+1。

●存在四个大素数r₁，r₂，s₁和s₂，使得r₁|p₁-1，s₁|p₁+1，r₂|p₂-1，s₂|p₂+1。

称r₁，r₂，s₁和s₂为三级素数，称p₁及p₂为二级素数，称p为一级素数。

为什么要采用强素数？这是因为p和q的取值会影响分解模数n的困难性。若p或q不是强素数，则可通过下面的p-1方法分解模数n。

假设p-1有k个素因子，由算术基本定理可得

其中，p_i为素数，a_i为正整数（i=1，2，…，k）。

如果p_i都很小，不妨设p_i＜B（B为已知的小整数），构造

其中，a≥max{a_i}，显然有（p-1）R。

因为任意小于素数p的正整数t均与p互素，不妨设t=2，由欧拉定理可知

t^φ（p）=2^φ（p）=2^（p-1）≡1（mod p）

因而t^R=2^R≡1（mod p）。计算X=t^R（mod n）=2^R（mod n），若X=1，则令t=3重新计算X，直到算出的X≠1。此时由gcd（X-1，n）=p，得到n的分解因子p和q。

【例5-8】 已知n=pq=150463，使用p-1方法分解n。

取B=8，a=3

则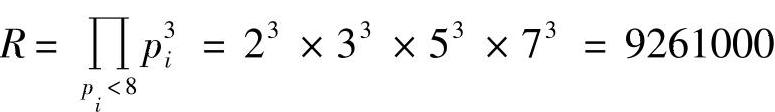

由于 2^R（mod n）≡139473

gcd（139473-1，150463）=379

所以n的分解式为150463=379×397

对于q也可以类似讨论。因此p-1和q-1必须有大素数因子，即p和q要为强素数。

RSA的安全性基于因子分解，故n的因子p和q必须选择恰当，以确保因子分解在计算上（有效时间内）不可能实现。

（2）p和q的位数差问题

当p和q的位数相差不大时，可通过下面的费马分解法分解模数n。设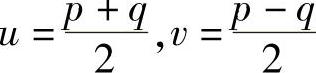

由于 （p-q）²=（p+q）²-4pq

则 u²-v²=n

因p和q的位数相差不大，则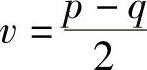将是一个很小的数，而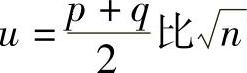稍大，这样可从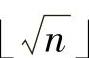开始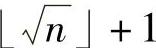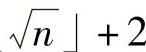，，⌊，…，依次尝试u，直到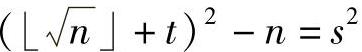为止。

通过

计算出p和q。

【例5-9】 已知n=pq=10403，使用费马方法分解n。

【解析】 由于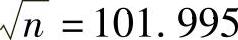

可令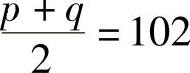

则 102²_-10403=1²

但若取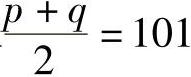，则101²-10403＜0

所以

解得 p=101，q=103

还可以将上面的步骤扩展为求t，s使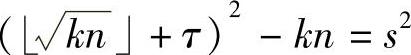。令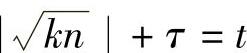，则t^2-s²=kn，即（t+s）（t-s）=kn。

【例5-10】 将141467分解为两个素数的积。

【解析】 由于

若求 （376-t）2-141467，t=1，2，3，…

将发现很不容易找到（376-t）2-141467正好是某一个整数的平方。

但有 3×141467=424401(www.xing528.com)

若从开始，则

故 141467=241×587

但是p和q的位数不能相差很大，若很大，可通过尝试法，从小的素数用依次试验的方法分解n。因此p和q的位数相差不能太大也不能太小，一般是几个比特。

（3）p-1与q-1的最大公因子要小

要求p-1与q-1的最大公因子要小是为了防止迭代攻击。假设攻击者截获了密文c=m^e（mod n），可以进行如下的迭代攻击。

记

其中，c₀=c，i=1，2，…。

若存在t使得

e^t（mod φ（n））≡1

则有整数k使e^t=k^φ（n）+1，那么由欧拉定理可知

与此同时还有

c_t≡c^e_t-1（mod n）

所以c^e_t-1（mod n）≡c≡m^e（mod n）

则m≡c_t-1（mod n）≡c^e_t-1（mod n）

如果t较小，则这种迭代攻击很容易成功。

【例5-11】 假设p=17，q=11，n=pq=187，e=7，明文为123，得到的密文为

c=123⁷≡183（mod 187）试用迭代攻击恢复明文。

如果计算

c₁=183⁷≡72（mod 187）

c₂=72⁷≡30（mod 187）

c₃=30⁷≡123（mod 187）

可见，只需对密文c再连续加密3次即可恢复明文。

由欧拉定理可知t=φ（φ（n））=φ（（p-1）（q-1）），若p-1与q-1的最大公因子较小，则t较大，如果t大到（p-1）（q-1）的一半，则迭代攻击难以奏效。

3.加密密钥e的选择

加密密钥e不能选得太小。对于明文m，密文c≡m^e（mod n），若e选得太小时，且m^e＜n，可直接将c开e次方得到明文m。加密密钥e要满足以下几个要求：

1）e要与模数n的欧拉函数值φ（n）互素，即gcd（e，φ（n））=1，否则无法计算解密密钥d。这一要求容易满足，现在已经证明两个随机数互素的概率约为3/5。

2）e不能太小，否则容易遭受低加密指数攻击。另外，如果e和m都很小且满足m^e＜n，此时密文c≡m^e（mod n）不需要经过模运算可直接得到，这样由c开e次方可得明文m。

3）e在模数φ（n）下的阶要足够大，即满足e^t（mod φ（n））≡1的最小正整数t要尽可能大，一般应达到（p-1）（q-1）/2。

RSA公钥密码体制中常常会出现不同模数n，却有共同加密密钥e的情形，此时的RSA容易受到指数攻击。

若有e个RSA密码体制RSA-n₁，RSA-n₂，…，RSA-n_e，都采用公钥e。

易见gcd（n_i，n_j）=1，i≠j

否则，可以求gcd（n_i，n_j），分解出n_i，n_j。

如果这t组密钥被用做加密同一个信息m，则

c₁≡m^e（mod n₁）

c₂≡m^e（mod n₂）

……

c_e≡m^e（mod n_e）

由中国剩余定理可得c≡m^e（mod n₁n₂…n_e）

m很小且满足m＜n₁，m＜n₂，…，m＜n_e

则m^e＜n₁n₂…n_e

于是得到m^e=c

从而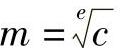

这样就恢复了明文。

4.解密密钥d的选择

为了提高解密效率，应尽可能设想选择较小的d，但可通过尝试法验证这种追求片面的利益是有安全隐患的。比如已知明文m，加密得到密文c≡m^e（mod n），可通过穷举d依次检验c^d≡m（mod n）是否成立。因此d不应选得太小，一般为d≥n¹/4。

加密密钥e选定之后，利用扩展的欧几里得算法可以求出解密密钥d。类似于对加密密钥e的要求，解密密钥d也不能太小，否则容易遭受已知明文攻击。

如果对明文m加密得到密文c，在解密密钥d很小的情况下，从某个正整数开始依次尝试，直接找出一个数t满足c^t（mod n）≡m，那么这个t就是解密密钥d。另外，Wiener于1990年利用连分数理论证明了当解密密钥d小于n¹/4时很容易分解模数n，然后可求出解密密钥d。因此，一般要求d不能小于n¹/4。