RSA算法解析：原理与应用

1.相关数学基础

在对RSA算法描述之前，先介绍它的相关数学基础。

（1）欧拉函数

欧拉函数是指对于一个正整数n，小于n且和n互素的正整数的个数，记为φ（n）。显然，对于素数p，φ（p）=p-1。对于两个素数p、q，它们的乘积n=p×q满足φ（n）=（p-1）×（q-1）。

【例5-1】 求φ（21）。

【解析】 比21小而与21互素的正整数有

{1，2，4，5，8，10，11，13，16，17，19，20}

总共12个，故

φ（21）=12

又由于 21=3×7

所以 φ（21）=（3-1）×（7-1）=12

（2）欧拉定理

若a和n互素，φ（n）为欧拉函数，则

a^φ（n）≡1（mod n）

【例5-2】 已知a=7，n=19，求aφ（n）（mod n）。

【解析】 7²≡11（mod 19）

7⁴≡7（mod 19）

7⁸≡11（mod 19）

7¹⁶≡7（mod 19）

由于n=19是素数，则有φ（19）=19-1=18。

（3）欧几里得算法

若a、b是两个正整数，令r₀=a，r₁=b，重复使用带余除法，即用每次的余数为除数去除上一次的除数，直至余数为0，可用如下方程来表示（其中，r_i是被除数，r_i+1是除数，r_i+2是余数，q_i+1是它们的商，i=0，1，2，…，m-1）：

最后一个不为0的余数是a和b的最大公因数gcd（a，b）。此算法的正确性，由以下结论来保证：

gcd（a，b）=gcd（b，a（mod b））

【例5-3】 求gcd（224，34）。

【解析】 gcd（224，34）=gcd（34，20）=gcd（20，14）=gcd（14，6）=gcd（6，2）=2

【例5-4】 求11^-1（mod 13）。

【解析】 由于13=11+2

2=13-11

11=5×2+1

1=11-5×2=11-5（13-11）=6×11-5×13

所以 11×6≡1（mod 13）

11^-1≡6（mod 13）

2.RSA算法的加密和解密

（1）参数定义和密钥生成

●选两个大素数p和q；（p、q保密）

●计算n=p×q，φ（n）=（p-1）×（q-1）；（n公开，φ（n）保密）

●随机选一整数e，满足1＜e＜φ（n），且gcd（φ（n），e）=1；（e公开）

●计算d，满足

d×e≡1（mod φ（n））

即d是e在模φ（n）下的乘法逆元，因e与φ（n）互素，由模运算可知，它的乘法逆元一定存在。（d保密）

（2）加密算法

加密时首先将明文比特串分组，使得每个分组对应的十进制数小于n，即分组长度小于log₂n，然后对每个明文分组m，作加密运算

c≡m^e（mod n）

（3）解密算法

对密文分组的解密运算为

m≡c^d（mod n）

下面证明RSA算法中解密过程的正确性。

证明：由加密过程知c≡m^e（mod n），所以

c^d≡m^ed（mod n）

≡m¹（modφ（n））（mod n）

≡m^kφ（n）+1（mod n）

下面分两种情况：

1）m与n互素，即gcd（m，n）=1，由欧拉定理得

mφ（n）≡1（mod n）

m^kφ（n）≡1（mod n）

m^kφ（n）+1≡m（mod n）

得c^d≡m（mod n）

2）gcd（m，n）≠1，先看gcd（m，n）=1的含义，由于n=pq，所以gcd（m，n）=1意味着m不是p的倍数也不是q的倍数。因此gcd（m，n）≠1意味着m是p的倍数或q的倍数，不妨设m=cp，其中c为一正整数。此时必有gcd（m，q）=1，否则m也是q的倍数，从而是pq的倍数，与m＜n=pq矛盾。(www.xing528.com)

由gcd（m，q）=1及欧拉定理得mφ（q）≡1（mod q），所以

m^kφ（q）≡1（mod q）

[m^kφ（q）]φ（p）≡1（mod q）

m^kφ（n）≡1（mod q）

因此存在一整数r，使得m^kφ（n）=1+rq，两边同乘以m=cp得

m^kφ（n）+1=m+rcpq=m+rcn

即m^kφ（n）+1≡m（mod n）

所以c^d≡m（mod n）

【例5-5】 在RSA公钥密码体制中，选定p=7，q=13，取e=5，当明文m=10时，求出d的值和相应的密文。

【解析】 由于n=p×q=7×13=91

则φ（n）=6×12=72

又de≡1（mod 72）

可求得d=e=1≡29（mod 72）

所以

c≡m^e（mod n）≡10⁵（mod 91）≡82（mod 91）

3.RSA的实现

（1）快速计算a^m（mod n）

RSA的加密/解密运算归结为求一个整数的方幂，再取模。如计算x¹⁶，若直接计算，则需做15次乘法；若按平方运算，即求x²，x⁴，x⁸，x¹⁶，则只需要4次乘法。

求模幂y=g^x（mod p）并不困难。设x的二进制表示为

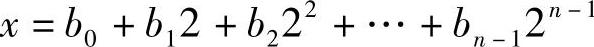（其中b_i为0或1）

则

式中，若b_i=0

则

若b_i=1

则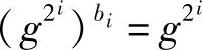

【例5-6】 求11⁷（mod 17）。

【解析】 由于7=2⁰+2¹+2²

则

故

11⁷（mod 17）≡11×2×4（mod 17）≡88（mod 17）≡3（mod 17）

计算y=g^x（mod p）的一种快速算法如下：

1）a←g，b←x，y←1；

2）若b=0，则输出y，算法终止；

3）若b是正的偶整数，则

a←a²（mod p），b←b/2，转3）否则转4）；

4）b←b-1，y←ay（mod p），转2）。

【例5-7】 用快速算法求11⁷（mod 17）。

【解析】 1）a←11，b←7，y←1

2）b←6，y←11

3）b←3，11²≡2（mod 17），a←2

4）b←2，2×11≡5（mod 17），y←5

5）b←1，2²≡4（mod 17），a←4

6）b←0，4×5≡3（mod 17），y←3

所以11⁷（mod 17）≡3

（2）快速产生大素数

一般来说，判定一个数是素数比较难，但否定它是素数要容易得多。例如，在数列{1，2，…，100}中，偶素数只有2这一个，故偶数可排除。同样，最后一位为5的数也不是素数。剩下的数列中第一个数3便是素数。再在余下的数列中，除去5的倍数，余下的第一个数7是素数。再从剩下的数列中除去7的倍数，现在剩下的数中第一个数11是素数，依此类推。

这种常规的筛选法判定n是否为素数，必须除以小于或等于的所有的素数，如果除不尽，就确定n是素数。当n的位数为100位或更大时，实际上是不可行的。

2002年印度数学家Agrawal等人提出了一种确定性的多项式算法，能直接判定n是否为素数，判定过程如下：

1）r←2；

2）当r＜n，转3）；

3）若gcd（n，r）≠1，则判定n是合数；

4）若r是素数，q是r-1的最大素数因子，若

否则转5）；

5）r←r+1，转2）；

6）对，若（x-a）n≠（nⁿ-a）mod（x^r-1），则n是合数；

7）n是素数。

这里log是以e为底的自然对数。