公钥密码体制思想详解

公钥密码体制的核心思想是加密和解密采用不同的密钥，这也是公钥密码体制和对称密码体制的最大区别。对于对称密码而言，密文的安全性完全依赖于密钥的保密性，一旦密钥泄露，将毫无保密性可言。但是，公钥密码体制彻底改变了这一状况。在公钥密码体制中，公钥是公开的，只有私钥是需要保密的。知道公钥和密码算法要推测出私钥在计算上是不可行的。这样，只要私钥是安全的，那么加密就是可信的。

显然，对称密码和公钥密码都需要保证密钥的安全，不同之处在于对密钥的管理和分发。在对称密码中，必须要有一种可靠的手段将加密密钥（同时也是解密密钥）告诉给解密方；而在公钥密码体制中，这是不需要的。解密方只需要保证自己的私钥的保密性即可，对于公钥，无论是对加密方而言还是对密码分析者而言都是公开的，故无需考虑采用可靠的通道进行密钥分发。这使得密钥管理和密钥分发的难度大大降低了。

公钥密码的基本思想与单向陷门函数的思想密切相关。从数学抽象的角度出发，单向陷门函数是一族应满足以下条件的可逆函数f_k：

●给定k和x，计算y=f_k（x）是容易的。

●给定k和y，计算x=f_k^-1（y）是容易的。

●给定y，但k未知时，计算x=f_k^-1（y）是不可行的。

设计公钥密码体制可以转换为寻找单向陷门函数。目前，人们主要是基于如下的数学上的困难问题来设计单向函数和公钥密码体制：

●大整数因子分解问题（如公钥密码体制RSA）；

●有限域上的离散对数问题（如公钥密码体制ElGamal）；

●椭圆曲线上的离散对数问题（如公钥密码体制ECC）。

一个公钥密码体制选择合适的单向陷门函数，由五元组{M，C，K，E，D}组成，且满足如下条件：

1）明文空间M，它是全体明文消息m的集合。(www.xing528.com)

2）密文空间C，它是全体密文c的集合。

3）密钥空间K，它是全体密钥k的集合，其中每一个密钥k均由公钥pk和私钥sk组成，即k=（pk，sk）。

4）对于K中的每一个密钥对k=（pk，sk），都存在E中的一个加密变换E_pk：M→C和D中的一个解密变换D_sk：C→M，使得任意明文消息m∈M都能找到一个唯一的c∈C满足c=E_pk（m），且m=D_sk（c）=D_sk（E_pk（m））。

5）对于所有的密钥对k=（pk，sk）∈K，由加密变换E_pk推出解密变换D_sk在计算上是不可行的。

针对公钥密码体制{M，C，K，E，D}的基本要求，一个可行的公钥密码算法应该满足如下要求：

1）接收方B产生密钥对k=（pk_B，sk_B）在计算上是容易的。2）发送方A用接收方B的公钥pk_B加密消息m产生密文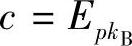（m）在计算上是容易的。

3）接收方B用自己的私钥sk_B解密密文c，还原明文消息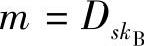（c）在计算上是容易的。

4）不仅攻击者由密文c和B的公钥pk_B恢复明文m是计算上不可行的，而且攻击者由B的公钥pk_B求解对应的私钥sk_B也是计算上不可行的。

5）加密/解密的次序可交换，即。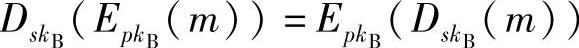

公钥密码算法以非对称的形式使用两个密钥，不仅能够在实现消息加/解密基本功能的同时简化了密钥分配任务，而且还对密钥协商与密钥管理、数字签名与身份认证等密码学问题产生了深刻的影响。可以说公钥密码思想为密码学的发展提供了新的理论和技术基础，是密码学发展史上的一次革命。