AES加密过程详解

Rijndael之所以能被选作高级加密标准，是因为该算法除具备低成本、高安全性的特性外，最大的优点在于即使在受限的工作环境下，如在较小的内存空间中，仍有很好的加密/解密运算效率，而且设计简单，对所有已知的攻击具有免疫性，如此便能保证AES有较长的安全周期。

1.AES的加密算法描述

在Rijndael的设计中，其算法的明文分组和密钥长度都有三个可选值，分别为128bit、192bit和256bit，产生的密文没有数据扩展。但在AES中，将明文和密文长度固定为128bit，密钥长度可以使用128bit、192bit和256bit三者中的任意一种，明文及加密过程的中间结果都称为状态State，状态State被表示成矩阵，矩阵的每个元素是1字节，并看成是有限域GF（2⁸）中的一个元素，矩阵的行数为4，列数为N_b。密钥被表示成4行N_k列的矩阵，N_k等于密钥长度比特数除以32，加密的轮数用N_r表示，如表4-10所示。

表4-10 N_r与N_b、N_k的关系

注：N_b=分组长度（bit）/32（bit）；N_k=密钥长度（bit）/32（bit）；N_r=加密的轮数

AES的加密算法没有采用Feistel结构，使用SP结构在每一轮使用代换和混淆并行处理整个数据分组。加密算法框图如图4-12所示，框图左边为AES加密算法的整体结构，右边为加密算法中的一轮变换，当N_k等于4时，整个算法由10轮组成。每轮由4个变换模块组成，分别是：字节代换（ByteSub）、行移位（ShiftRow）、列混合（MixColumn）、密钥加（AddRoundKey），最后一轮略有不同，没有列混合。

加密过程描述如下：

1）初始轮密钥加。给定一个明文M和种子密钥K₀，将它们以矩阵排列并进行异或加法运算。

2）N_r-1轮迭代。对前N_r-1轮中的每一轮，用S盒进行一次字节代换操作（ByteS-ub）；对代换的结果做行移位操作（ShiftRow）；接着做列混合变换（MixColumn）；再进行密钥加（AddRoundKey）操作。轮迭代中的密钥K_i由种子密钥K₀通过密钥扩展算法产生。

3）最后一轮变换。最后一轮变换与前面各轮稍有不同，依次进行ByteSub、ShiftRow和AddRoundKey操作。

图4-12 AES加密算法框图

a）AES算法的整体结构 b）AES算法的一轮变换

2.加密轮变换

AES的加密轮变换主要由4个不同的变换模块组成，用伪C语言描述如下：

最后一轮变换与前面各轮不同，将MixColumn这一步去掉，其伪C语言代码如下：

（1）字节代换（ByteSub）

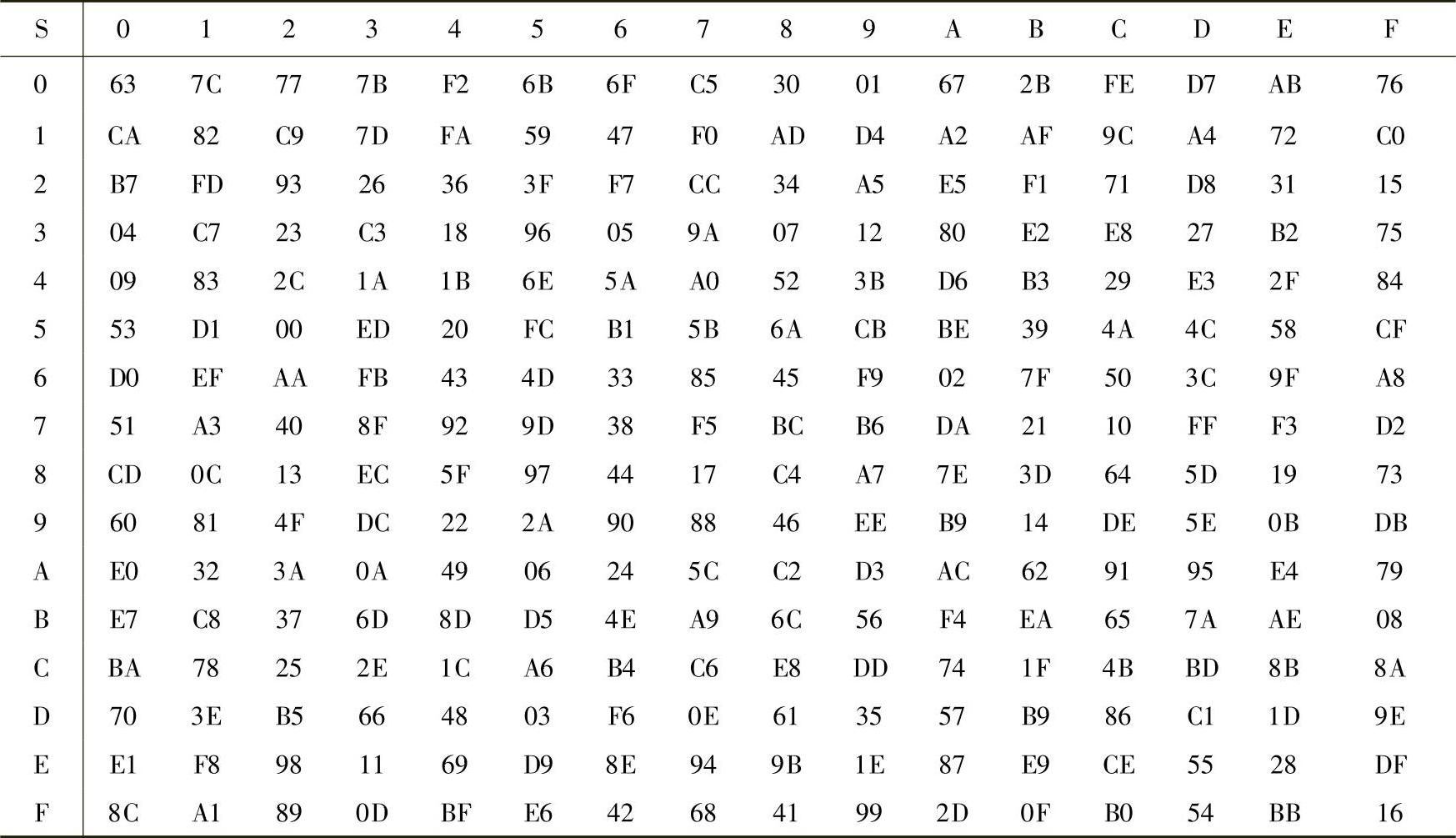
字节代换ByteSub（State）是一个关于字节的非线性变换，可以使用S盒查表得到输出。AES定义了一个S盒，如表4-11所示，它是由16×16字节组成的方形表，包含了8位值所能表示的256种可能的变换。对于已知的某字节作为S盒的输入，把该字节的高4位作为行号，低4位作为列号，查表4-11取出S盒中对应行列交叉点的元素作为输出。例如，S（8C）=64，S（B3）=6D。

当N_k等于4时，AES中的State是一个4行4列的矩阵，字节代换是一个简单的S盒查表操作，如图4-13所示。

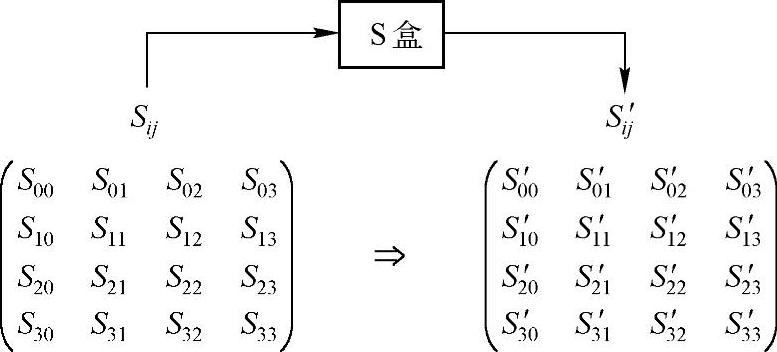
图4-13 S盒字节代换

【例4-13】 设当前的State为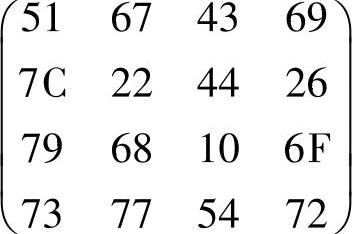，计算ByteSub（State）。

查表4-11知S（51）=D1，S（67）=85，依此类推，所有字节查表完成可得

S盒是可逆的，由以下两个变换的合成得到：

首先，将字节X看做GF（2⁸）上的元素，变换成自己的乘法逆元T。

T≡X^-1mod（x⁸+x⁴+x³+x+1）

其次，对字节T作GF（2）上的仿射变换：

Y=A·T⊕B

AES用矩阵以如下的方式来描述这个仿射变换：

其中， ，

从而S（X）=A·X^-1⊕B

表4-11 AES加密算法的S盒

（2）行移位（ShiftRow）

在行移位变换中，状态矩阵State中的每一行将以字节为单位，循环左移不同的位移量。图4-14描述行移位变换方法，State的第一行保持不变，第二行循环左移1字节，第三行循环左移2字节，第四行循环左移3字节。

图4-14 行移位变换方法

【例4-14】 设当前的State为，计算ShiftRow（State）。

按图4-14所示的行移位变换方法可得

（3）列混合（MixColumn）(www.xing528.com)

列混合变换将State乘以一个固定的矩阵A，对State逐列进行变换，每一列中的每个字节被变换成一个新值，直到4列都变换完毕。相乘后得到的乘积矩阵，其中每个元素均是一行和一列中所对应元素的乘积之和。这里的乘法和加法都是定义在有限域GF（2⁸）上的。

【例4-15】 设当前的State为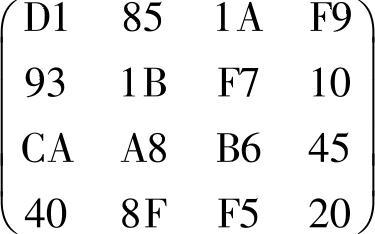，计算MixColumn（State）。

对于乘积结果矩阵中的第一列，计算如下：

第一列中的第一个字节9D通过如下方式计算而得

在AES中，列混合变换也可以用数学上的多项式来计算。MixColumns（State）对一个状态逐列进行变换，它将一个状态的每一列视为有限域GF（2⁸）上的一个多项式。

在列混合变换中，每一列所表示的多项式将乘以一个固定的多项式A（x），模多项式为（x⁴+1），多项式A（x）定义如下

A（x）={03}x³+{01}x²+{01}x+{02}

（4）密钥加（AddRoundKey）

密钥加是将轮密钥K_i简单地与状态State进行逐比特异或。轮密钥K_i由种子密钥K₀通过密钥扩展算法得到，将状态State表示为矩阵A_i-1，与轮密钥K_i的密钥加运算为

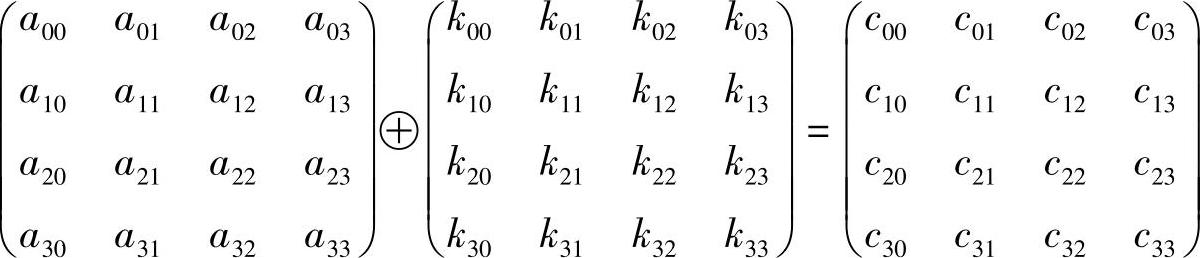
【例4-16】 列混合后的结果A_i-1与轮密钥K_i分别为

求轮密钥加后的结果C_i。

3.密钥扩展算法

密钥扩展算法可将种子密钥K₀通过一定的运算得到整个加密过程中所有的轮密钥，原理如下：

●种子密钥通过密钥扩展算法被扩展成扩展密钥；

●轮密钥从扩展密钥中取，其中第1轮轮密钥取扩展密钥的前N_b个字，第2轮轮密钥取接下来的N_b个字，如此下去；

●轮密钥的比特数总和等于分组长度乘以轮数加1，如分组长度为128bit，轮数为10时，轮密钥的比特数总和为

128bit×（10+1）=1408bit

用伪C语言描述N_k≤6的密钥扩展算法如下

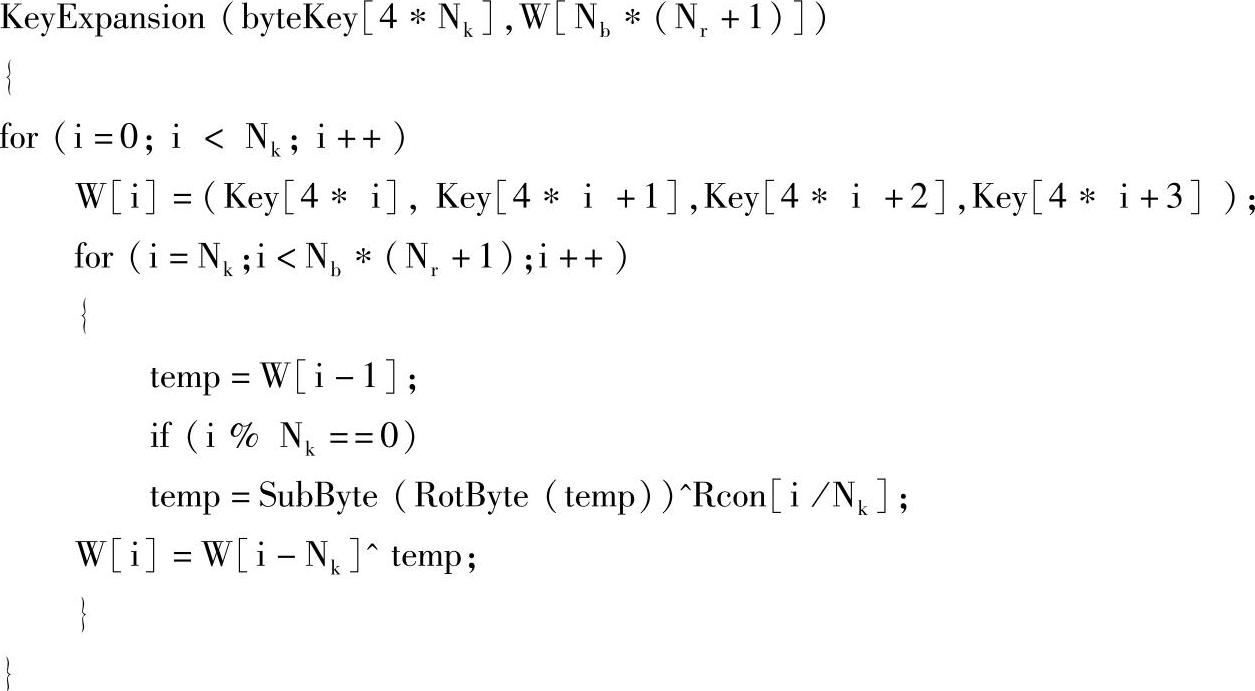
以上算法中，由密钥扩展算法将种子密钥扩展成扩展密钥的计算过程如下：

当种子密钥长度为128bit时，这里的N_k=4，其中，

temp=SubByte（RotByte（W[i-1]））⊕Rcon[i]

RotByte（）表示循环左移1字节，如W=（a₀，a₁，a₂，a₃），则RotByte（W）=（a₁，a₂，a₃，a₀）；

SubByte（）是S盒的字节代换；

Rcon[i]为轮常数，定义为

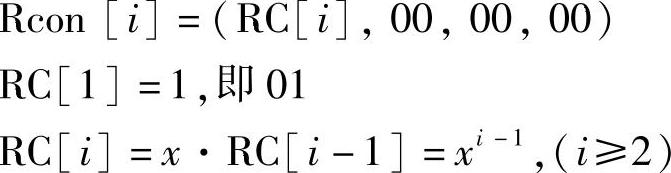
字节用十六进制表示，同时为GF（2⁸）上的元素，其中x^i-1为GF（2⁸）域中的多项式x的i-1次方所对应的字节。由于x对应的字节为02，上式也可以写为

Rcon[i]=（（02）i^-1，00，00，00）

【例4-17】 在AES加密算法中，假定种子密钥K₀的长度为128bit，它的值为

K₀=06 07 08 09 0A 0B 0C 0D 0E 0F 00 01 02 03 04 05

计算第1轮的子密钥K₁的值。

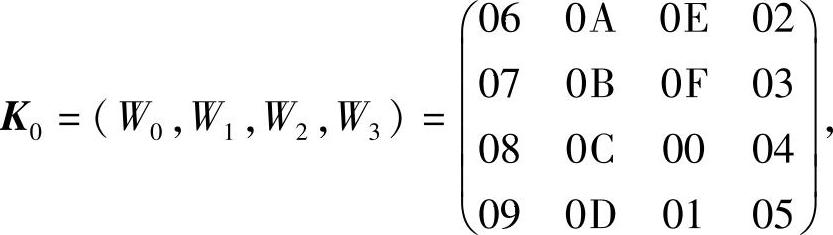
其中，

根据密钥扩展算法可计算出：