DES加密过程详解

DES的结构是典型的Feistel密码结构，其中明文分组长为64bit，64bit的明文通过DES加密算法生成64bit的密文，输入初始种子密钥为64bit，其中，第8、16、24、32、40、48、56、64为奇偶校验位，实际的密钥长为56bit。

DES的加密过程如图4-4所示，整个过程由三个阶段来完成，首先是一个初始置换IP，用于重排明文分组的64bit数据。然后是具有相同功能的16轮迭代，每轮中都有置换和代换运算，第16轮变换的输出分为左、右两半，并交换次序。最后再经过一个逆初始置换IP^-1（为IP的逆）从而产生64bit的密文。

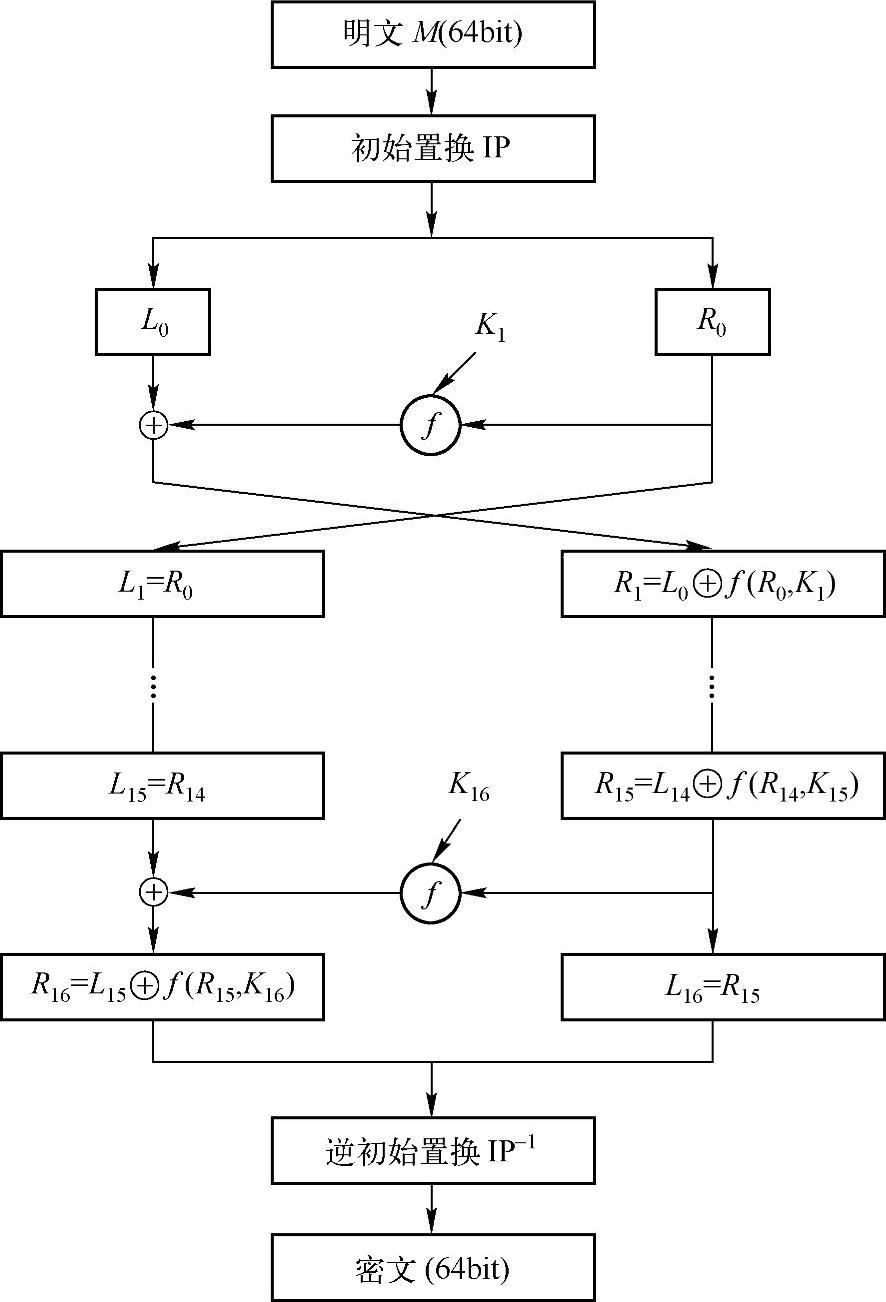
图4-4 DES加密算法框图

1.初始置换IP

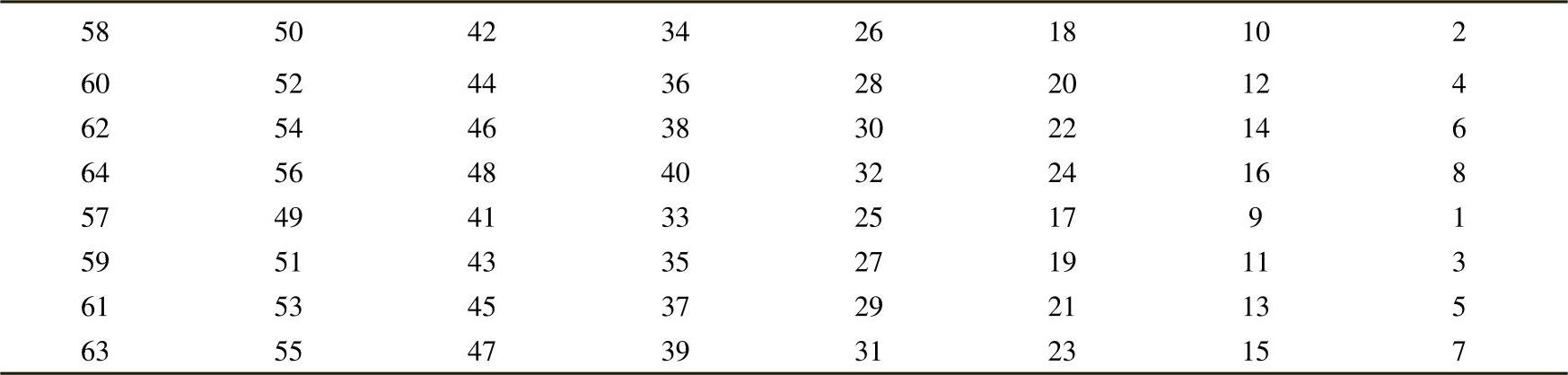
初始置换IP如表4-1所示，主要是对64bit的明文M中各位进行换位，打乱明文中各位的排列次序。经过IP置换，明文中原有的m₅₈放在第1位，m₅₀放在第2位，依此类推，m₇放在第64位。

输入64bit的明文M（m₁，m₂，m₃，…，m₆₄），通过IP置换得到

X（m₅₈，m₅₀，m₄₂，…，m₇）

这里X=IP（M）。

表4-1 初始置换IP

【例4-1】 设明文

M=（0123456789ABCDEF）₁₆

=（0000000100100011010001010110011110001001101010111100110111101111）₂

经过IP置换，并分成左、右两部分，结果为

L₀=11001100000000001100110011111111

R₀=11110000101010101111000010101010

2.轮结构

64bit的明文M经过初始IP置换后分成左、右两部分，记为L₀和R₀，各32bit，经过16轮迭代后再输出。每轮迭代的结构和Feistel加密结构一样，如图4-5所示。其数学公式为：

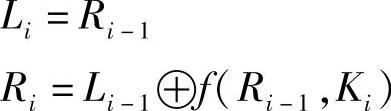
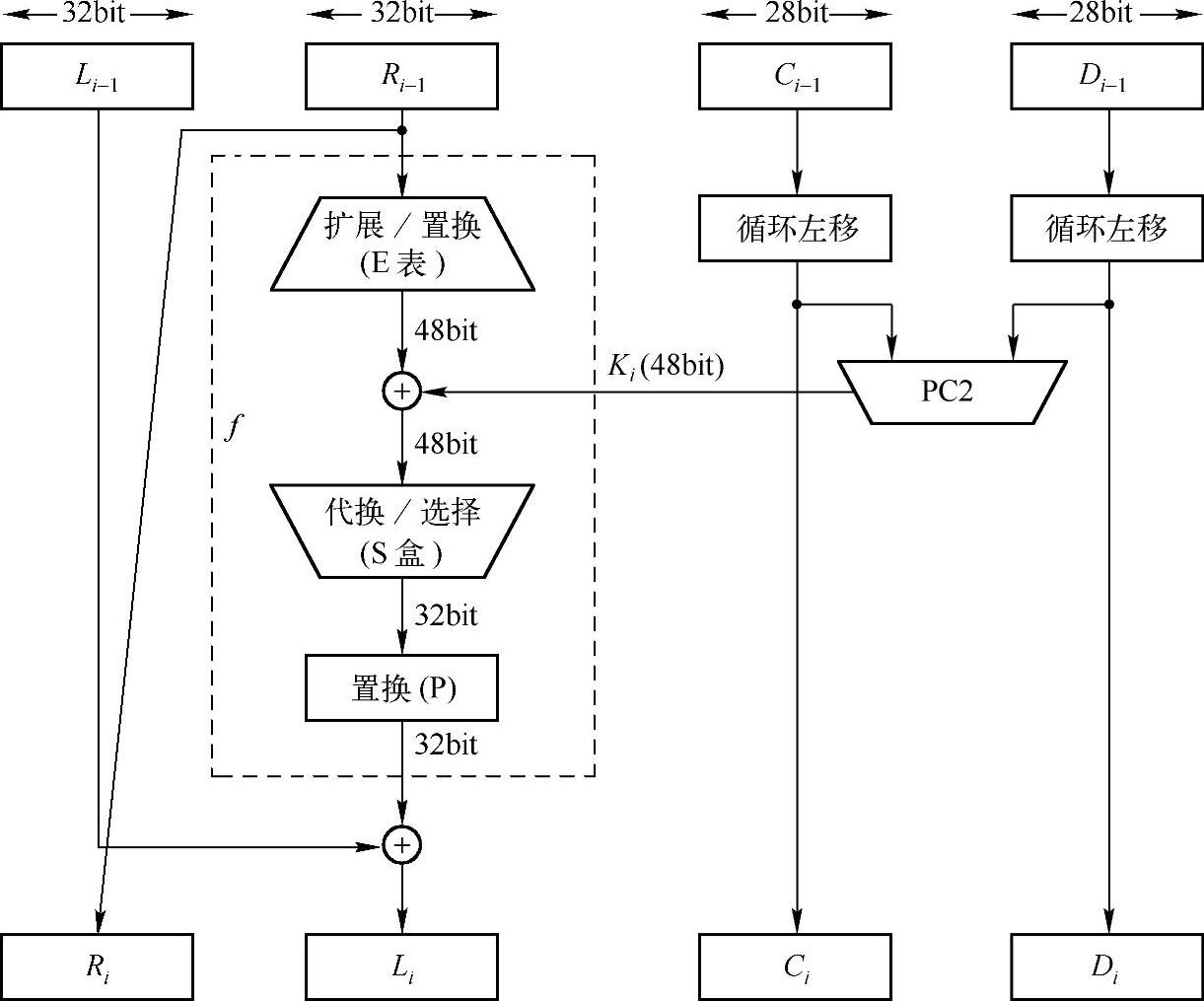
图4-5 DES加密算法的轮结构

式中，f（R_i-1，K_i）是第i轮的轮函数（图中虚线框）；⊕表示两个比特串的异或；L_i-1，R_i-1表示第i-1轮的左、右两部分；L_i，R_i表示第i轮的左、右两半；K_i是第i轮用的子密钥。

将第i-1轮的密钥K_i-1分成C_i-1和D_i-1两部分，各28bit，循环左移后，经过置换选择PC2，形成第i轮的子密钥K_i（48bit），该密钥作为轮函数f（R_i-1，K_i）的一个输入参数。

轮结构中的核心是f（R_i-1，K_i）函数，它是每轮实现混乱和扩散的关键模块。其基本加密结构如图4-6所示。

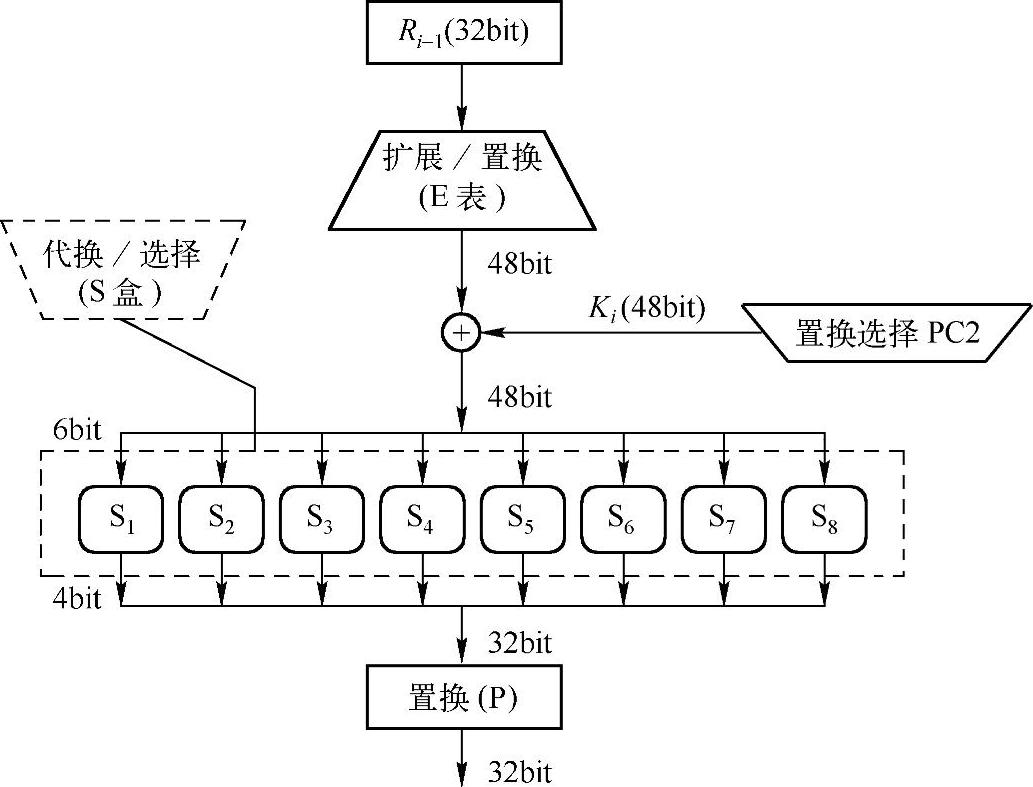
图4-6 轮函数结构框图

图中的子密钥K_i为48bit，f（R_i-1，K_i）的输入R_i-1为32bit，经E表扩展置换成48bit，该48bit与置换选择PC2产生的子密钥K_i（48bit）进行异或运算，运算的结果输入S盒，形成32bit的输出，最后经过P置换后即为函数f（R_i-1，K_i）的输出。

不难看出，f（R_i-1，K_i）函数的执行过程包括扩展置换E表、代换选择S盒、置换P表。子密钥K_i是f（R_i-1，K_i）的输入参数。

（1）子密钥K_i的生成

子密钥K_i的生成大致分成三个过程：置换选择PC1，循环左移，置换选择PC2。如图4-7所示，初始密钥K为64bit，首先置换选择PC1置换后，接着将置换后的56bit分为各28bit的左、右两半，分别记为C₀和D₀。在第i轮分别对C_i-1和D_i-1进行循环左移，移位后的结果作为求下一轮子密钥的输入，同时也作为置换选择PC2的输入。通过置换选择PC2产生的48bit的K_i，即为第i轮的子密钥，作为函数f（R_i-1，K_i）的输入。

1）置换选择PC1：输入初始密钥K为64bit，其中第8、16、24、32、40、48、56、64为奇偶校验位，对剩下的56bit密钥按表4-2通过置换PC1进行重新编排，并将编排后的56bit分为各28bit的左、右两半，分别记为C₀和D₀。

【例4-2】 设初始密钥

K=(123DAB779F658067）₁₆

=(00010010 00111101 10101011 01110111 10011111 01100101 10000000 01100111)₂

经过置换选择PC1，并分成左、右两部分，结果为

C₀=0101010 0101010 0010101 1100001

D₀=1001110 1101110 1000010 1101011

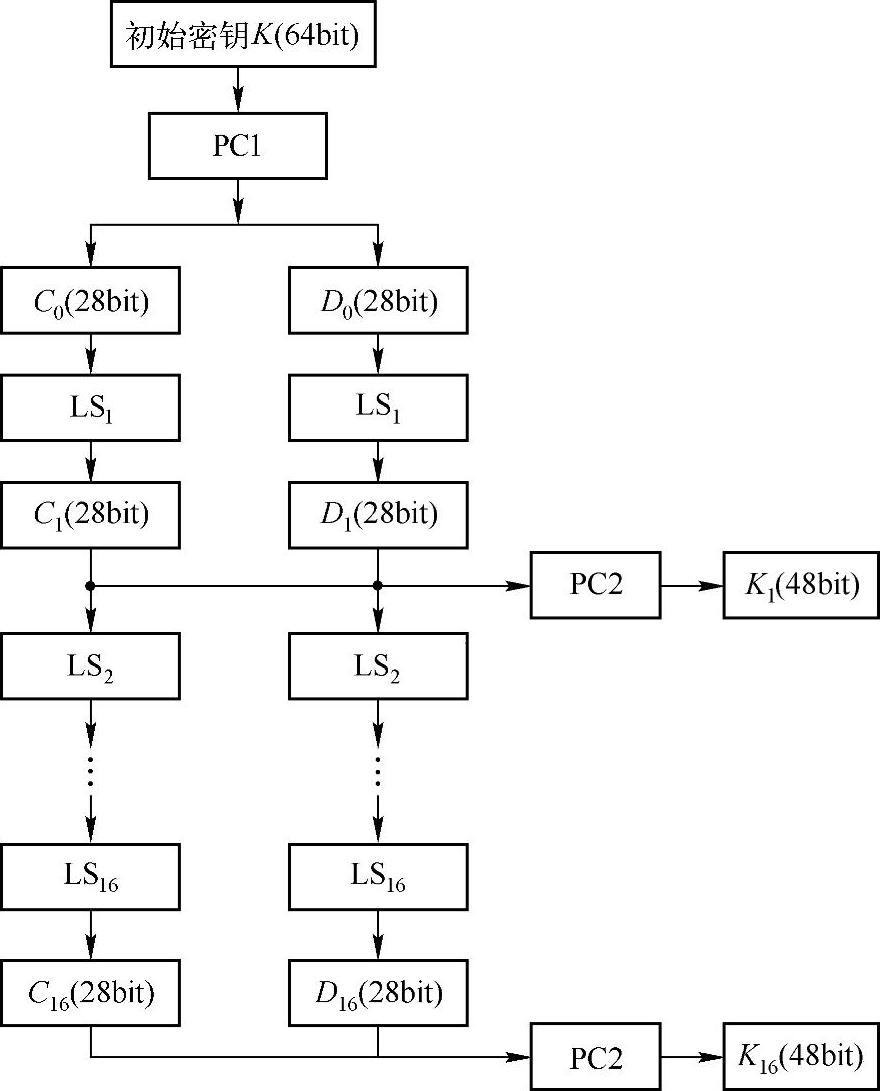
图4-7 子密钥生成过程

2）循环左移：对每个i，1≤i≤16，计算C_i=LS_i（C_i-1），D_i=LS_i（D_i-1），其中LS_i表示一个或两个位置的左循环移位。当i=1，2，9，16时，则左移一个位置，其余左移两个位置。如表4-3所示。

表4-2 置换选择PC1

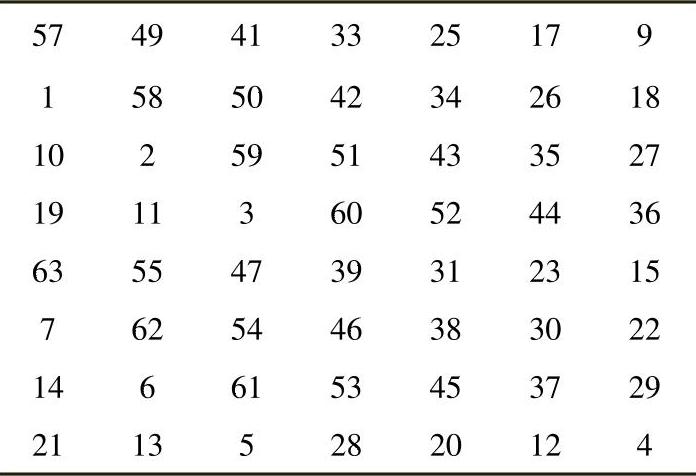
表4-4 置换选择PC2

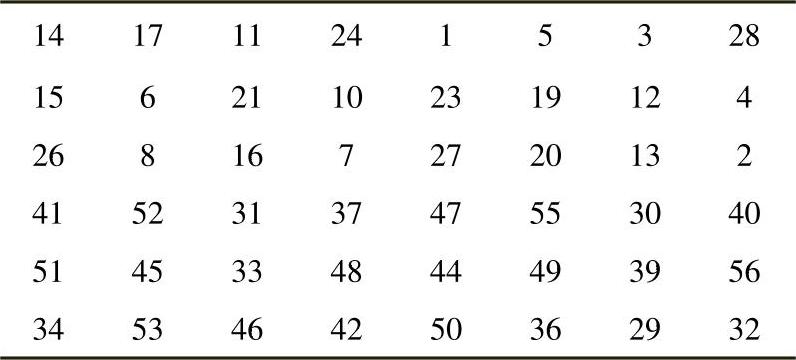
表4-3 循环左移LS

【例4-3】 接例4-2，若

C₀=0101010 0101010 0010101 1100001

D₀=1001110 1101110 1000010 1101011

计算C₁=LS₁（C₀），D₁=LS₁（D₀），即将C₀、D₀循环左移一位后，得

C₁=1010100 1010100 0101011 1000010

D₁=0011101 1011101 0000101 1010111

3）置换选择PC2：按表4-4中的置换选择PC2，对连接在一起的C_iD_i进行重新编排，其作用是将56bit的C_iD_i置换成48bit，成为第i轮迭代的子密钥K_i。

【例4-4】 接例4-3，若

C₁=1010100 1010100 0101011 1000010

D₁=0011101 1011101 0000101 1010111(www.xing528.com)

经过置换选择PC2，生成的48bit子密钥K₁为

K₁=000011 100011 001001 101100 011011 010010 011100 011101

（2）扩展置换E

扩展置换E的功能是将32bit的R_i扩展成48bit。扩展置换E将32bit的输入分成8组，每组4bit，经置换E的扩展后，变成每组6bit输出，如表4-5所示。扩展后的结果与子密钥K_i进行异或运算，结果作为S盒的输入。

表4-5 扩展置换E

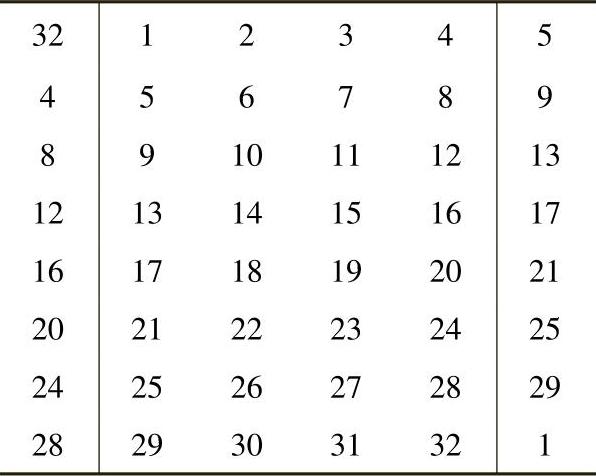
表4-6 P盒置换表

【例4-5】 接例4-1和例4-4，若

R₀=11110000 10101010 11110000 10101010

K₁=000011 100011 001001 101100 011011 010010 011100 011101

经过扩展置换E得

E（R₀）=011110 100001 010101 010101 011110 100001 010101 010101

E（R₀）⊕K₁=011101 000010 011100 111001 000101 110011 001001 001000

（3）S盒代换

DES算法中除了S盒是非线性变换外，其余变换均为线性变换，DES算法保密的关键在于S盒。S盒是经过精心设计和严格挑选的，美国国家安全局（NSA）曾公布了下列几条设计准则：

●S盒的每一行是整数0，1，…，15的一个置换；

●没有一个S盒是它输入变量的线性函数；

●改变S盒输入中的某1bit，至少引起2bit的输出变化；

●对任一S盒的任何两个输入x和x⊕001100，则对应的输出至少有2bit不同；

●对任一S盒的任何两个输入x和x⊕11ab00（其中a，b属于{0，1}），则对应的输出至少有2bit不同；

●任一S盒的6bit输入，若某1bit输入保持不变，当其他5bit输入变化时，则输出中的0与1数目分布的总数接近相等。

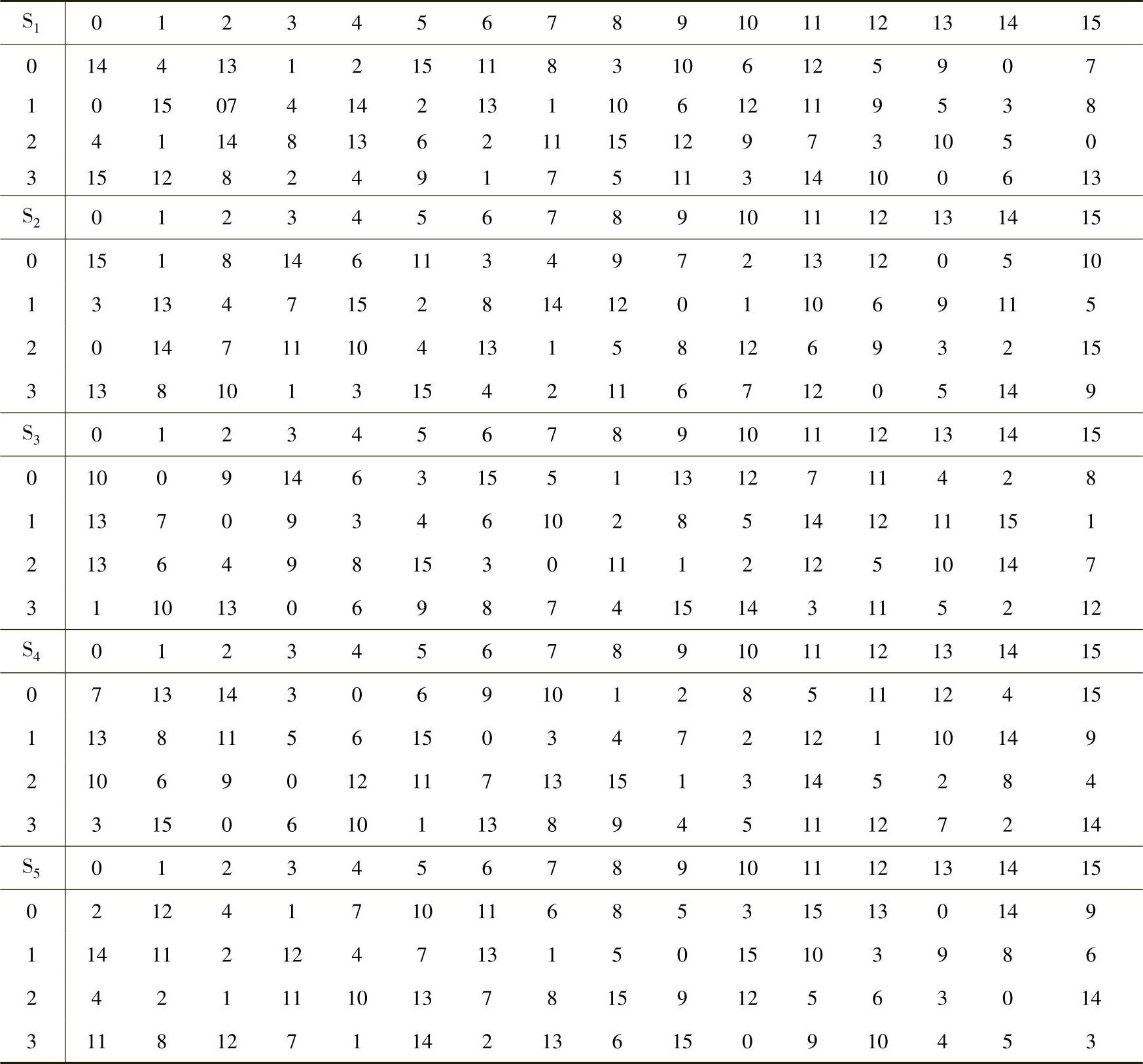
轮函数中的代换由8个S盒组成，每个S盒的输入长为6位、输出长为4位，如表4-7所示。对于S_i盒，其6位输入中，第1位和第6位形成一个2位二进制数，用来选择S_i的行，中间4位用来选择列。行和列选定后，得到其交叉位置的十进制数，将这个数表示为4位二进制数即得这一S盒的输出。

【例4-6】 S₁的输入为011001，行选为01（即第1行），列选为1100（即第12列），行列交叉位置的数为9，其4位二进制表示为1001，所以S₁的输出为1001。

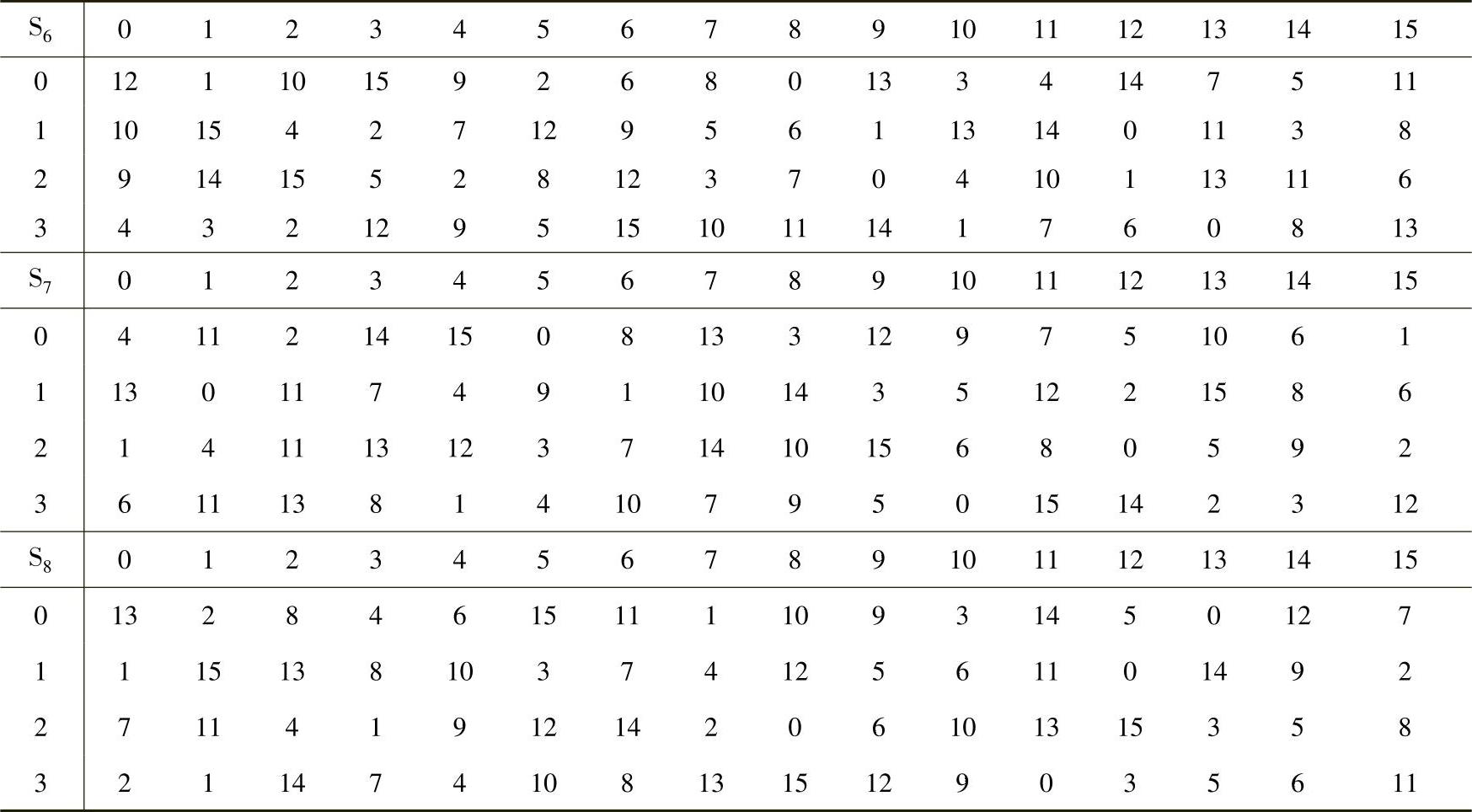
表4-7 DES的S盒

（续）

【例4-7】 接例4-5，已知

E（R₀）⊕K₁=011101 000010 011100 111001 000101 110011 001001 001000作为S盒的输入，经S盒代换输出32bit，结果为

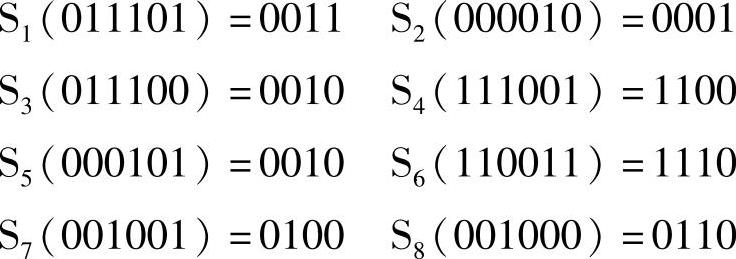
（4）P盒置换

P盒置换将S盒的32bit输出重新按表4-6进行排列，排列后的32bit即为函数f（R_i-1，K_i）的输出。

【例4-8】 接例4-7，S盒的32bit输出为

S（E（R₀）⊕K₁）=0011 0001 0010 1100 0010 1110 0100 0110

再经过P盒置换得到函数f（R₀，K₁）的输出如下

f（R₀，K₁）=00010000 00110010 01010010 11101110

在例4-1中，已知

L₀=11001100 00000000 11001100 11111111

又例4-8中，f（R₀，K₁）=00010000 00110010 01010010 11101110

通过如下运算可得到第1轮迭代输出结果的左、右两部分为

R₁=L₀⊕f（R₀，K₁）=11011100 00110010 10011110 00010001

L₁=R₀=11110000 10101010 11110000 10101010

依此类推，可以得出其他各轮的运算结果。经过16轮迭代，最后一轮（第16轮）迭代输出结果的左、右两部分为：

R₁₆=01110010 00010011 01001111 10010011

L₁₆=10001111 01011110 00000011 10111100

3.逆初始置换IP^-1

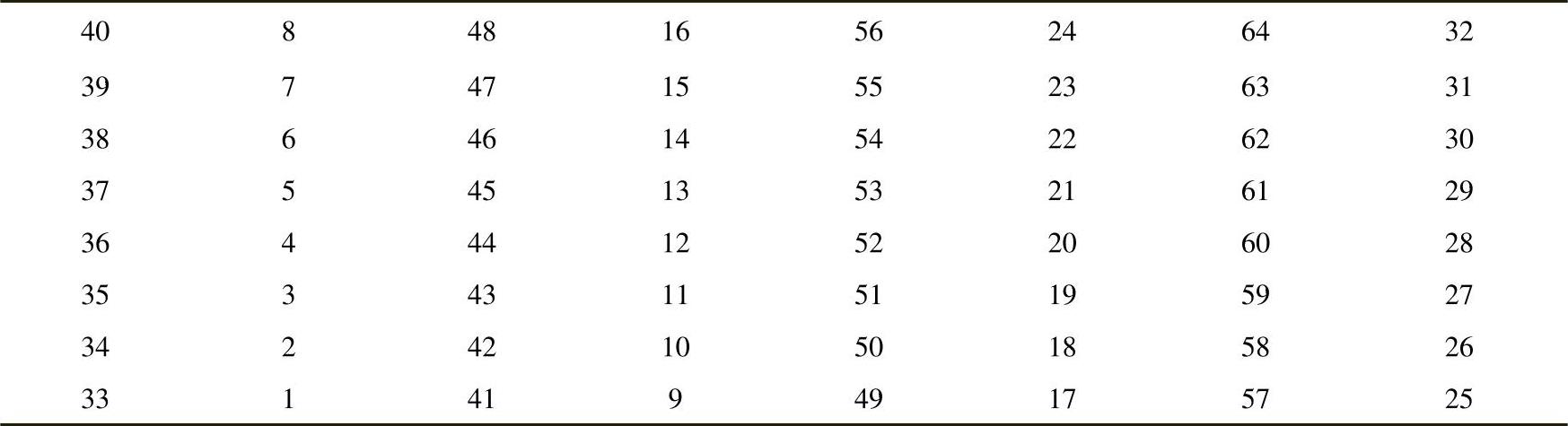
DES算法经过16轮迭代后，最后一步是逆初始置换，该置换IP^-1如表4-8所示，将第16轮迭代的输出经过逆初始置换IP^-1处理得到密文C，即

C=IP^-1（R₁₆L₁₆）

表4-8 逆初始置换IP^-1

【例4-9】 已知第16轮迭代输出结果的左、右两部分为

R₁₆=01110010 00010011 01001111 10010011

L₁₆=10001111 01011110 00000011 10111100

C=IP^-1（R₁₆L₁₆）=10011101 11111101 10100110 10100110 01110011 01000010 01100100 10000011