分组密码的算法结构详解介绍

目前，分组密码所采用的整体算法结构主要有Feistel结构和SP结构。Feistel结构与SP结构的主要区别在于：SP结构的每轮迭代改变整个数据分组；而Feistel结构的每轮迭代只改变输入分组的一半。

1.Feistel结构

Feistel结构把任何函数（一般称F函数，又称轮函数）转化为一个置换，它是由Horst Feistel设计Lucifer分组密码时构造的。图4-2是Feistel结构示意图，加密算法的输入是一个分组长度为2n的明文M₀和一个种子密钥K₀，将明文M₀分成左右两半L₀和R₀，这里L₀是M₀的左半部分nbit，R₀是M₀的右半部分nbit，在进行完r轮迭代后，左右两半再合并到一起以产生密文分组C=R_rL_r。其中第i轮迭代的输入为前一轮输出的函数。根据下列规则计算L_i和R_i（1≤i≤r）：

其中，F是轮函数；⊕表示两个比特串的异或；K_i是第i轮用的子密钥，由种子密钥K₀得到。

加密/解密相似是Feistel结构分组密码的一个实现优点，但Feistel结构分组密码的扩散似乎有些慢，例如需要两轮才能改变输入的每一比特。数据加密标准（Data Encryption Standard，DES）是这种密码结构的代表。

2.SP结构(www.xing528.com)

SP结构是Feistel结构的一种推广，其结构清晰。S一般称为混淆层，是由密钥控制的非线性置换，通常由并行查表（S盒）实现，主要起混淆作用。P一般称为扩散层，通常由与密钥无关的可逆线性变换实现，主要起扩散作用。SP结构框图如图4-3所示。

图4-2 Feistel结构示意图

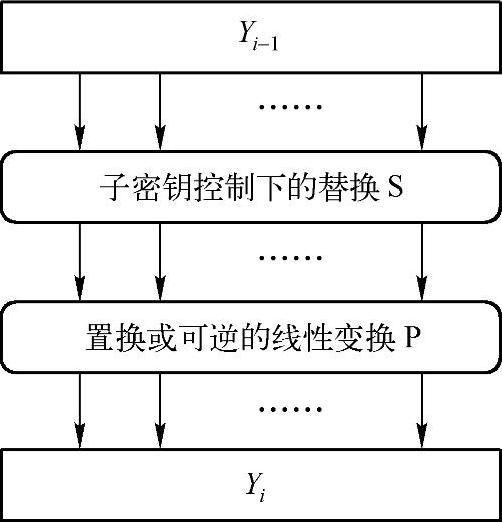
图4-3 SP结构框图

SP结构与Feistel结构相比，SP结构分组密码的加密/解密算法通常不相似，且它的抗线性攻击和抗差分攻击的能力容易衡量，扩散速度快，因此许多著名的密码算法，如高级加密标准（Advanced Encryption Standard，AES）等，都采用了SP结构。