产生二元序列级数最少的线性移位寄存器的级数称为该序列的线性复杂度。n级m序列的线性复杂度为n。对于一个线性复杂度为n的二元周期序列来说，只要知道该序列中任意相继的2n位就可确定整个序列以及产生该序列的LFSR的结构（即特征多项式或反馈函数）。因此，虽然线性移位寄存器产生的m序列具有良好的伪随机特性，但如果其直接作为密钥序列，并应用二元加法进行加密，则在知道移位寄存器的位数n及其2n位明文流与对应的密文流时，就可以推出移位寄存器的特征多项式，破解应用此LFSR的二元加法流密码。具体分析如下。
根据LFSR输出序列{ai}的递推关系
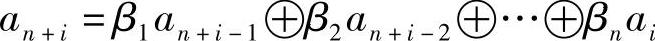
如果以输出流ai直接作为密钥流，即
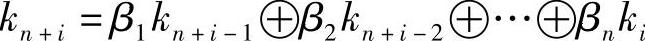
在此方程中，将反馈系数β1，β2，…，βn看做未知数，如果能够用已知的密钥流ki构建一个关于β1，β2，…，βn的线性方程组，则有可能解出n个反馈系数，从而得到反馈函数。要使这个线性方程组有唯一解，则需要如下n个方程构成方程组：
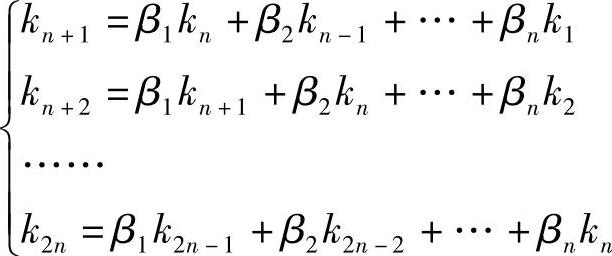
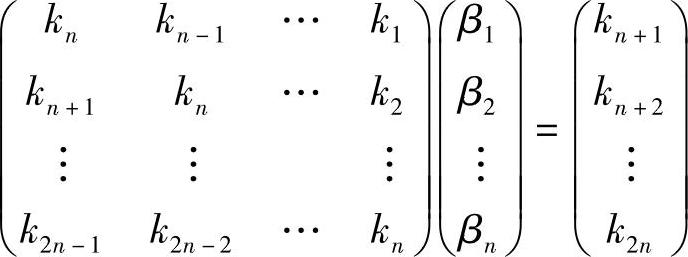
写成矩阵形式为
(www.xing528.com)
因此
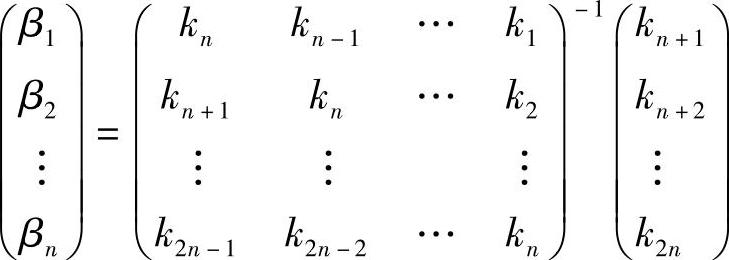
从以上分析可知，要确定反馈系数，需要知道LFSR的位数n及其2n个密钥位串。对于二元加法流密码来说，只要知道2n个明文位串m1，m2，…，m2n及其对应的密文位串c1，c2，…，c2n，则它们的异或可以得出2n个密钥位串，即ki=mi⊕ci（i=1，2，…，2n）。
【例3-10】 已知一个3位的LFSR，明文串为01101001100001及其相应的密文串11001110100100，则计算出相应的密钥串为10100111000101。由密钥串中前6比特可建立如下方程
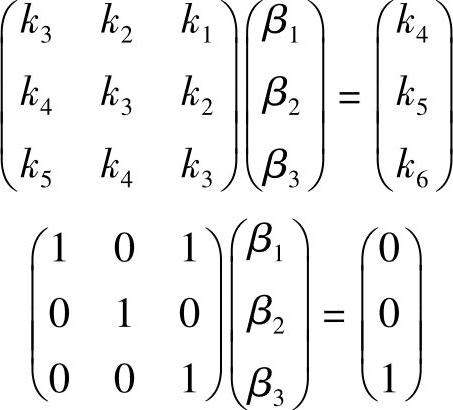
解出β1=1，β2=0，β3=1。这个LFSR的结构如图3-12所示，其特征多项式为p（x）=x3+x+1。
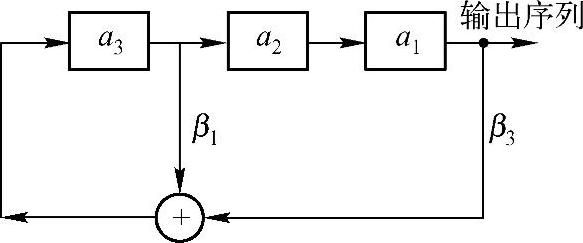
图3-12 一个3位的LFSR
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
