线性反馈移位寄存器的工作原理

生成密钥流序列的通用方法为利用一个有限长的种子产生具有足够长周期的、随机性良好的序列。只要生成方法和种子都相同，就会产生完全相同的密钥流。移位寄存器（Shift Register）结构简单，易于实现且运行速度快，是普遍应用的一个重要方法。

移位寄存器由一系列串接的二值{0，1}存储单元构成，n个存储单元构成n位移位寄存器。按照确定的时钟周期，移位寄存器的每一位都向右移一位，最右边的位作为输出，最左边的位被输入位取代。图3-8显示了一个6位移位寄存器在输入一个0之后的移位操作。

显然，要使移位寄存器生成较长的随机流作为密钥流，需要有随机的输入位序列。这部分功能由反馈函数实现。n位移位寄存器的状态由每一位上的值构成的有限域GF（2）上的n维向量（a₁，a₂，…，a_n）描述。反馈函数是移位寄存器的当前状态的函数，其将移位寄存器的当前状态经过函数计算后，将结果作为下一时间周期的输入，致使移位寄存器的每一位向右移，状态发生变化。可具体描述如下。

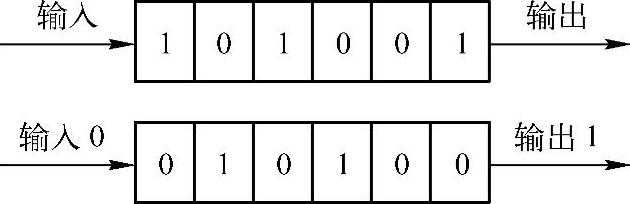
图3-8 移位寄存器的移位操作

设移位寄存器的当前状态为

s_i=（a_i，a_i+1，…，a_i+n-1）

则

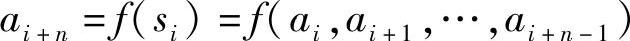
将a_i+n作为移位寄存器的输入，代替第n个位置上的值，而驱使寄存器的所有位向右移，达到新的状态

s_i+1=（a_i+1，a_i+2，…，a_i+n）

且输出a_i。由此可以得到序列a₁，a₂，…，a_n，…。

显然，当移位寄存器的反馈函数f是a₁，a₂，…，a_n的线性函数时，称移位寄存器为线性反馈移位寄存器（LFSR）；否则，为非线性反馈移位寄存器（NLFSR）。

线性移位寄存器的反馈函数f可表示为

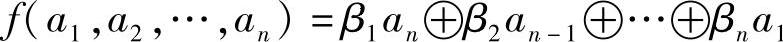
其中，β_i=0或1（i=1，2，…，n）称为反馈系数，其中至少有一个非零，一般总假定β_n=1。β₁，β₂，…，β_n的作用就相当于一个开关，用断开和闭合来表示0和1，这样的线性函数共2ⁿ个。

线性反馈移位寄存器如图3-9所示。图中标有a₁，a₂，…，a_n-1，a_n的小方框表示二值{0，1}存储单元，可以是一个双稳触发器，信号流从左向右。这n个二值存储单元称为该线性反馈移位寄存器的级。在任一时刻，这些级的内容构成该线性反馈移位寄存器的状态。

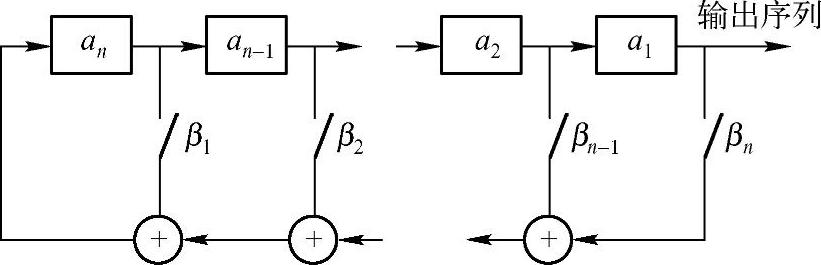
图3-9 n级线性反馈移位寄存器

【例3-6】 有一个6级线性反馈移位寄存器如图3-10所示。其中初始状态为（0，1，1，0，1，0），则LFSR在各时刻的状态如表3-3所示。从表中可以看出，输出序列为

0 1 0 1 1 0 1 0 0 1 0…周期为8。

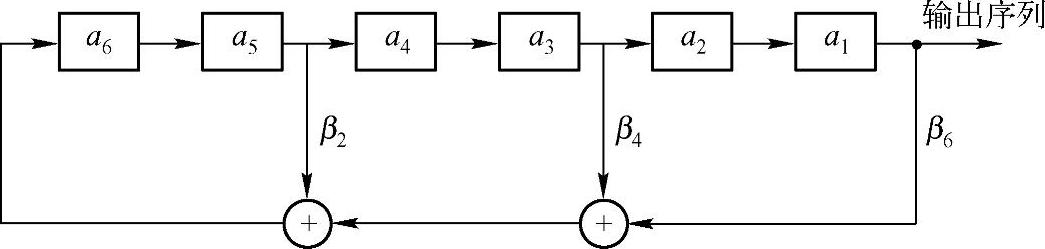
图3-10 一个6级线性反馈移位寄存器(www.xing528.com)

表3-3 LFSR状态表

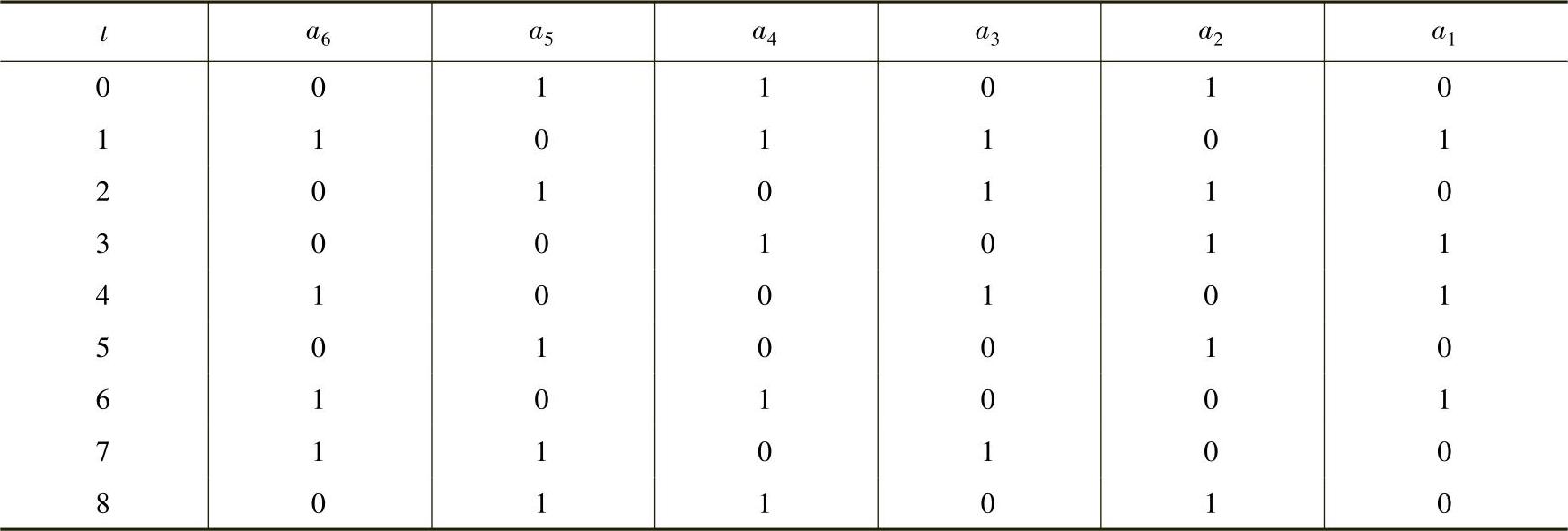
用LFSR产生随机性好的密钥流，需要LFSR的输出流的周期足够长。因此，需要研究对一个给定的LFSR，可生成的序列的最长周期为多少，以及在什么情况下，能够保证产生最长周期序列。以便在设计时能够利用尽可能小的LFSR产生周期长、统计性能好的序列。对于n位的LFSR，最多有2ⁿ个状态（这是一个重复排列问题，每个位置上有两个可取元素0或1）。在线性运算下，全“0”的状态不会转移到其他状态，实际中不会让寄存器出现全“0”状态。因此，n位的LFSR最多会有2ⁿ-1个状态。在反馈函数确定的情况下，每一种状态对应一个确定的输入和输出，相同的状态产生相同的输入和输出，一旦出现状态重复，便会使产生的输出序列重复。因此，n位LFSR能够产生的序列的最长周期为2ⁿ-1。

n位LFSR产生的周期为2ⁿ-1的序列被称为该LFSR的m序列。m序列具有良好的伪随机性，满足Golomb随机性的三个假设。因此，设计能够产生m序列的LFSR具有重要的现实意义，也是设计中需要解决的关键问题。实际中，LFSR的输出序列的周期取决于初始状态和反馈模式。

LFSR的输出序列{a_i}满足以下递推关系：

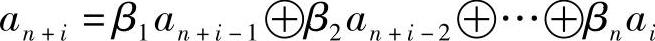
其中，i为正整数。

这种递推关系描述了LFSR的数学结构，可用一个GF（2）上的一元n次多项式表示

称此多项式为n位LFSR的特征多项式。

图3-10所示的LFSR的特征多项式为p（x）=x⁶+x⁴+x²+1。

【例3-7】 已知一个4级LFSR的特征多项式为p（x）=x⁴+x³+1，请表示它的线性反馈移位寄存器循环结构图。

特征多项式为p（x）=x⁴+x³+1的LFSR循环结构如图3-11所示。

对于多项式p（x），能够被其整除的多项式x^k_-1的最小的k称为p（x）的周期或阶。可以证明，一个n位LFSR能够产生m序列的充要条件是其特征多项式p（x）的阶为2ⁿ-1的不可约多项式（即本原多项式）。

【例3-8】 设f（x）=x⁴+x³+x²+x+1是GF（2）上的不可约多项式，但它不是m序列。

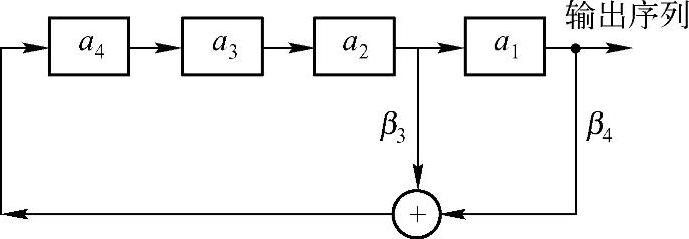
图3-11 一个4级的LFSR

因为一次多项式x，x+1不能整除f（x），则三次多项式也不能整除f（x）。二次多项式x²，x²+1，x²+x也不能整除f（x），相应地，二次不可约多项式x²+x+1不能整除f（x）可直接验证。

以f（x）为特征多项式的LFSR的输出序列可由

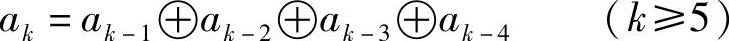
和初始状态求出。

设初始状态为0001，则输出序列为000110001100011…，周期为5，不是m序列。