了解有限状态自动机：状态转移与输出的数学模型

有限状态自动机（Finite State Machine，FSM或者Finite State Automaton，FSA），也称为有限自动机，表示有限个状态以及在这些状态之间的转移和动作等行为的数学模型。有限状态自动机包含有限个状态，一定状态下的输入会产生状态的转移和输出。有限状态集、输入字符集、输出字符集、转移函数、输出函数为有限状态自动机的主要构件。

有限状态机一般用一个多元组表示，例如六元组（∑，Γ，S，s₀，δ，ω），其中

●∑是有限输入字符集；

●Γ是有限输出字符集；

●S是非空有限状态集；

●s₀是初始状态，为S中的元素；

●δ：S×∑→S是状态转移函数；

●ω：S×∑→Γ是输出函数。

可以使用多种类型的状态转移表描述转移函数和输出函数，从而表示有限状态机。也可用有向图表示有限状态机，称为状态转移图（或转移图）。状态转移图的顶点对应自动机的状态，边对应输入、输出有序对。

【例3-4】 设S={s₁，s₂，s₃}，∑={σ₁，σ₂，σ₃}，Γ={γ₁，γ₂，γ₃}，表3-2给出了此有限状态机的状态转移表，图3-7为对应的状态转移图。(www.xing528.com)

表3-2 状态转移表

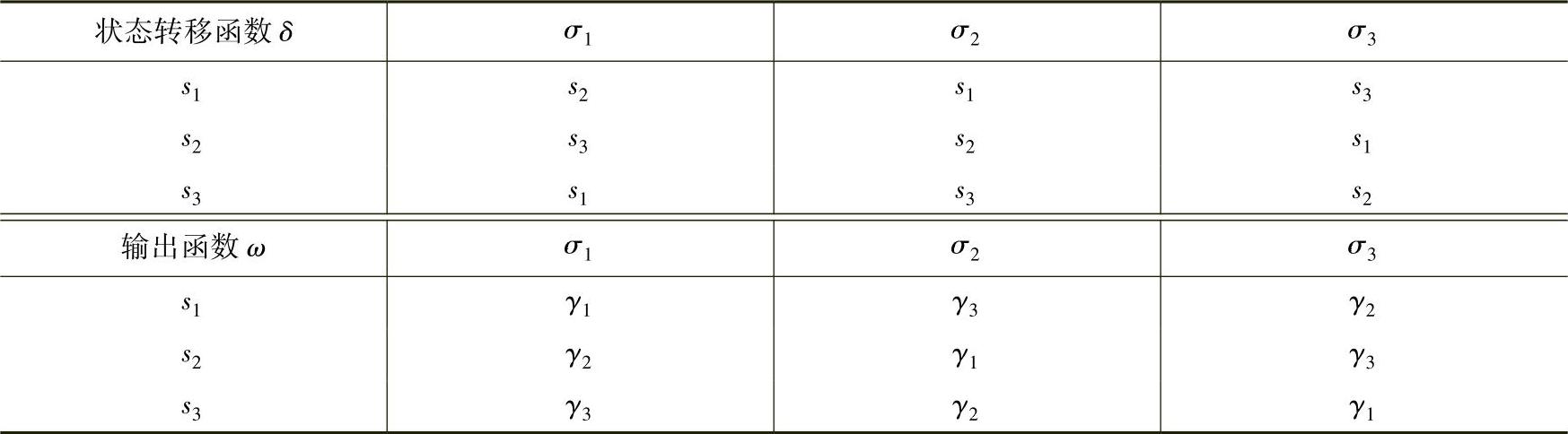
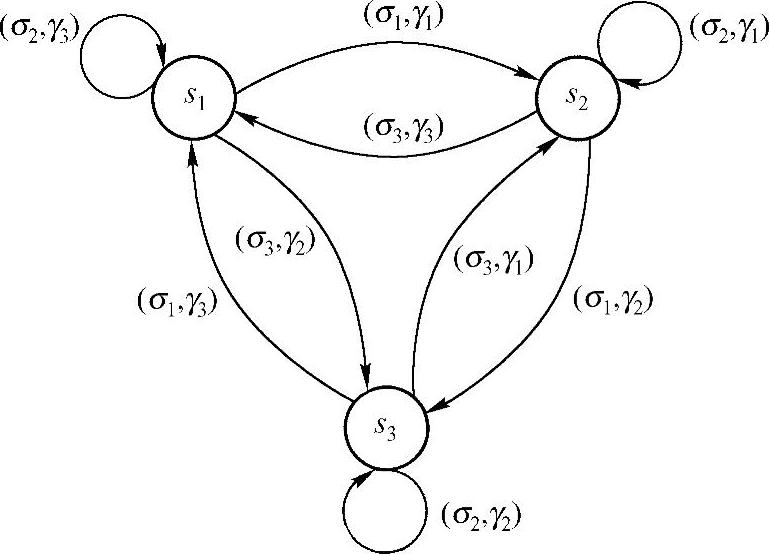
图3-7 状态转移图

【例3-5】 在例3-4中，若输入字符序列为σ₁σ₂σ₁σ₃σ₃σ₁，初始状态为s₁，则得到的状态序列为

s₁s₂s₂s₃s₂s₁s₂

输出字符序列为

γ₁γ₁γ₂γ₁γ₃γ₁

流密码的关键是密钥流生成器，由图3-5和图3-6知，可以将密钥流生成器看做有限状态自动机，其输入字符集为种子密钥k*。对于同步密钥流生成器，函数f为状态转移函数，h为输出函数。对于自同步密钥流生成器，状态为前t个时刻的密文字序列，状态转移函数为密文字序列在时间为t的窗口内的滑动，即若s_i=（c_i-t，c_i-t+1，…，c_i-1），则s_i+1=δ（s_i）=（c_i-t+1，c_i-t+2，…，c_i）。