如何使用多字母替代密码提高账号安全性？

单一字母替代密码表现出明文中单字母出现的频率分布与密文中相同，多字母替代密码使用从明文字母到密文字母的多个映射来隐藏单字母出现的频率分布，每个映射是简单替代密码中的一对一映射，多字母替代密码将明文字母划分为长度相同的消息单元，称为明文分组，对明文成组地进行替代，同一个字母有不同的密文，改变了单一字母替代密码中密文的唯一性，使密码分析更加困难。

多字母替代密码的特点是使用了两个或两个以上的替代表。著名的Vigenere密码和Hill密码等均是多字母替代密码。

1.Vigenere密码

Vigenere密码是最古老而且最著名的多字母替代密码体制之一，这种密码体制被视为最安全的简单多字母替代密码。

该密码体制有一个参数n。在加密/解密时，把英文字母映射为0～25的数字再进行运算，并按n个字母一组进行变换。明文空间、密文空间及密钥空间都是长度为n的英文字母串的集合。Vigenere密码加密/解密算法定义如下：

设密钥k=（k₁，k₂，…，k_n），明文m=（m₁，m₂，…，m_n），则加密算法为

E_k（m）=（c₁，c₂，…，c_n）

其中：c_i≡（m_i+k_i）（mod 26），i=1，2，…，n。

对密文c=（c₁，c₂，…，c_n），解密算法为

D_k（c）=（m₁，m₂，…，m_n）

其中：m_i≡（c_i-k_i）（mod 26），i=1，2，…，n。

【例2-6】 设密钥KEYS，明文消息为GOODCRYPTOSYSTEM，试用Vigenere密码对其进行加密，然后再进行解密。

【解析】 为了表述更加清楚，本例的密文用小写字母，明文和密钥用大写字母。

由密钥KEYS，得n=4，密钥对应的数字序列为（10，4，24，18）。然后将明文按每4个字母进行分组，并转换这些明文字母为相应的数字，再用模26加上对应密钥数字，其加密过程如表2-2所示。

表2-2 Vigenere密码加密过程示例

得到的密文为：qsmvmvwhdsqqcxce。

解密时，使用相同的密钥，但用模26减法代替模26加法，可以解密出明文。具体解密过程留给读者完成。

Vigenere密码的加密/解密算法也可以采用如表2-3所示的字母方块。使用Vigenere密码对明文消息加密时，需要根据密钥选择所使用的行，从而使用不同的行来替代明文消息中的每个字母得到密文。例如，在例2-6中，明文字母“G”对应的密文为“q”，即Vigenere字母方块中G列和K行的交叉点字母“q”。字母“O”对应的密文为“s”，即方块中O列和E行的交叉点字母“s”，依此类推，也可以得到全部的密文。

表2-3 Vigenere字母方块

（续）

2.Hill密码

Hill密码的基本思想是将明文字母通过线性变换，将它们转换为个数相同的密文字母。Hill密码使用的密钥是一个n×n的整数矩阵，加密算法是C≡K×M（mod p），解密时只需做一次逆变换即可。

给定一个具有m个字母的明文，选定一个n值，n＜m，将密钥K构造为一个n×n的矩阵。将m个字母的明文划分为n个字母的多个组，n个字母转换为整数列向量M，通过矩阵乘法C≡K×M（mod p）得到向量C，随后将向量C中的整数转换为密文。

【例2-7】 设明文消息为seed，试用n=2，密钥的Hill密码对其进行加密，然后再进行解密。(www.xing528.com)

【解析】 这里m=4，选择n=2，将明文划分为两组：（s，e）和（e，d）。选定从“a”到“z”的26个字母，并且分别为这些字母分配从0到25的整数值，如表2-1所示。（s，e）和（e，d）的数字为（18，4）和（4，3）。其加密过程如下：

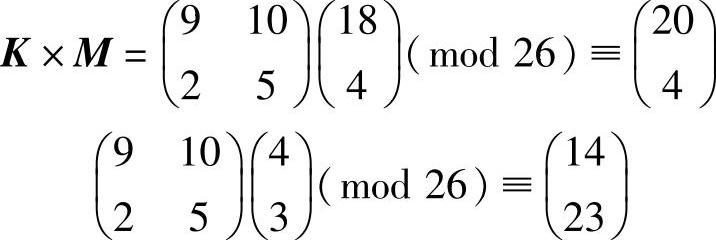
将加密后得到的数字（20，4），（14，23）转换为字母ueox，即seed的加密结果是ueox。显然，明文不同位置的字母“e”加密成的密文字母不同。

执行矩阵运算M≡K^-1×C（mod p）可以完成解密操作。本例中K的逆矩阵K^-1=，解密过程如下：

将解密操作后得到的数字（18，4），（4，3）转换为字母，由此得到正确的明文“seed”。

Hill密码的安全性在于：

●可以较好地抑制自然语言的统计特性，不再有单字母替换的一一对应关系，对抗唯密文攻击有较高安全强度。

●密钥空间较大，在忽略密钥矩阵K可逆限制条件下，K=26n×n。Hill密码的脆弱性在于：

●若提供的矩阵M是可逆的，则能计算出K≡CM^-1（mod 26），从而破译该密码体制。

●若方阵M关于模26不可逆，攻击者可通过尝试其他明文密文对来产生新的方阵M，直到找到一个可逆的明文矩阵M就可破译Hill密码。

3.一次一密密码

若多字母替代密码的密钥是一个随机且不重复的字符序列，这种密码则称为一次一密密码，因为它的密钥只使用一次。该密码体制是美国电话电报公司的Joseph Mauborgne在1917年为电报通信设计的一种密码，又称为Vernam密码。Vernam密码在对明文加密前首先将明文编码为（0，1）序列，然后再进行加密变换。

设m=（m₁m₂m₃…m_i…）为明文，k=（k₁k₂k₃…k_i…）为密钥，其中：m_i、k_i∈（0，1），i≥1，则

加密变换为

c=（c₁c₂c₃…c_i…），其中c_i=m_i⊕k_i，i≥1

解密变换为

m=（m₁m₂m₃…m_i…），其中m_i=c_i⊕k_i，i≥1

在应用Vernam密码时，如果对不同的明文使用不同的随机密钥，这时Vernam密码为一次一密密码。

【例2-8】 设明文消息是10111001，密钥（随机序列中的一段）是00101011，那么加密过程如下

由于每一密钥序列都是等概率随机产生的，敌手没有任何信息用来对密文进行分析。香农从信息论的角度证明了这种密码体制在理论上是不可破译的。但如果重复使用同一个密钥加密不同的明文，则这时的一次一密密码就较为容易破译。

若敌手获得了一个密文c=（c₁c₂c₃…c_i…）和对应明文m=（m₁m₂m₃…m_i…）时，就很容易得出密钥k=（k₁k₂k₃…k_i…），其中k_i=c_i⊕m_i，i≥1。

实际上，一次一密体制属于流密码，加密/解密方法都使用异或，这使软、硬件实现都非常简单。虽然这种密码体制在理论上是不可破译的，然而在实际应用中，真正的一次一密体制却受到很大的限制，其主要原因在于一次一密体制需要非常长的密钥序列，需要花费相当大的代价去产生、传输和保存，且密钥不允许重复使用。这样，分发和存储这样的随机密钥序列，并确保密钥的安全都是很困难的；另外，如何生成真正的随机序列也是一个现实问题。一般情况下，选择一个短的随机输入产生一个伪随机序列作为密钥序列，称为“近似”的一次一密乱码本。