矢量信号分析的技术背景探析

在现代通信网络中，数字通信克服了信道带来的各种不利影响，同时能够提高频谱资源的利用率，并具有较高的保密性能。正是由于其抗干扰性好、保密性强、容量大等诸多特点已成为现代通信的基本形式。数字调制解调技术的应用场合很多，包括无线通信、广播电视、卫星通信等各种通信系统以及军事通信中的扩频通信、通信对抗等。

经过几十年的发展，出现了很多数字无线通信系统，例如：GSM蜂窝移动通信系统、CDMA蜂窝移动通信系统、无线寻呼系统、数字集群通信系统等。各种数字无线通信系统的信号调制方式也越来越多，如QPSK、DQPSK、π/4DQPSK、SPSK、DSPSK、16QAM、MSK、GMSK等。无线通信系统的多址方式从采用频分多址（FDMA）技术的第一代模拟系统发展到以第二代数字移动通信为主体的时期（主要是GSM技术，采用时分多址技术），采用CDMA技术的第三代移动通信系统也于2009年在我国全面商用。特别是代表未来数字移动通信方向的OFDM/MIMO技术，也是高度依赖数字调制技术的。各种数字无线通信系统的符号速率也不相同，例如GSM信号符号速率为270.8333333 kSymbol/s、CDMA2000信号的符号速率为1.228 8 MSymbol/s、WCDMA信号的符号速率为3.86 MSymbol/s。

通信技术的迅速发展对相应的测试技术提出了更新更高的要求，特别是针对第三代移动通信系统、Wi MAX系统等，这要求测量的频谱带宽达到5～20 MHz，相邻信道泄漏功率比达-70 dBc，同时对TDMA及CDMA系统中连续载波或突发载波的测量等，都是传统的测量手段所难以实现的。在调制域，要想实现既数字化又直观的调制参数测量，需要矢量解调分析仪表。

矢量信号分析技术就是通过正交解调和分析，同时结合其他分析方法的分析测试技术。复杂的数字射频通信系统需要精确地测量各种参数，测量一般包括4个方面：功率测量、频率测量、时序测量和调制准确度测量。功率测量包括载波功率、邻近信道功率、突发脉冲功率等的测量。频率测量包括载波频率、占用带宽等的测量。时序测量主要针对脉冲信号，包括脉冲重复周期测量、上升时间测量、下降时间测量、占空比测量等。矢量调制误差参量衡量的是实际调制信号偏离理想信号的程度，包括误差矢量幅度、I/Q幅度误差、I/Q相位误差、I/Q原点偏移等。矢量信号分析仪能够完成上述的测量任务，特别是精确分析数字调制信号的各种误差，为电路和系统设计提供理想的测试手段。

在现代无线通信网络中，数字传输方式的采用克服了无线信道带来的各种不利影响，同时能够提高频谱资源的利用率，并具有较高的保密性能。数字通信系统的发展对测试提出了新的要求。矢量信号分析仪就是近年来随着数字通信的发展而产生的一种新型信号测量分析仪器。矢量信号分析仪作为一种新型的测试仪器，可以满足用户对复杂数字调制信号的测试，为无线通信设备提供完整的测量解决方案。

矢量信号分析仪扩大了频谱分析仪所具有的功能，提供了在整个微波频段进行测量的能力，能进行快速、高分辨率的频谱测量、解调以及先进的时域分析，非常适合于表征一些复杂信号，如通信、电视、广播、声呐和超声成像中所使用的猝发脉冲、瞬变信号和已调信号。矢量信号分析仪也能进行深入的调制分析，由于能捕获到信号的幅度和相位，矢量信号分析仪特别适于分析数字调制信号，对各种复杂的数字调制信号进行定性定量的衡量，提供既精确又直观的调制参数测量结果。

图3-14　正交解调的基本模型

在当代数字通信系统中，通信信号的种类很多，如ASK、FSK、MSK、GMSK、PSK、DPSK、OPSK、QAM等等，从理论上来说，各种通信信号都可以用正交调制的方法加以实现。同样，对于几乎所有的调制样式，都可以采用正交（I/Q）解调法进行解调。如图3-14所示为正交解调的基本模型。利用两路对称的解调电路将输入的射频信号直接变换到基带信号（I分量和Q分量），该功能的实现是建立在将输入射频信号功分并与两路正交90°的本振信号混频的基础上的。正交90°的本振信号是为了获得I分量和Q分量，随后的低通滤波器是为了滤除混频的高频分量。

对于连续波复合调制，已调信号的数学表达式为：

式中，fc为信号载波频率，A（t）为幅度调制，θ（t）为相位调制。s（t）与本地载波进行正交混频，并分别经过低通滤波后得到两路正交分量，s（t）与被测信号经模拟前端接收并由ADC数字化后进行数字混频和数字抽取滤波，完成信号的捕获，并将捕获数据存储在捕获RAM中，在完成数据存储后，通过数字信号处理（DSP）实现测量信号的矢量分析。

本地载波频率为f0，在实际解调中必须与信号载频同频同相，否则解调输出就会严重失真。(www.xing528.com)

采用模拟混频器方式的I/Q解调电路存在着一些不容易克服的问题，如增益不平衡、本振泄漏、本振不正交、直流偏移、阻抗失配等。

在实际运用中，信号的处理基本上采用数字化方式，从而有效克服模拟混频中I、Q两路的不平衡等缺点。数字正交解调的基本模型如图3-15所示。A/D转换器采样时钟满足奈奎斯特抽样定理，采样后的信号形式为：

式中，ωc为信号载波的角频率。图3-15中的h（n）为数字低通滤波器的冲激响应，两路是完全相同的。最后得到的两路正交信号分别为：

图3-15　数字正交解调原理框图

传统的正交解调电路采用模拟器件，由此引入的一系列模拟器件所固有的误差降低了正交解调器的性能，例如增益平衡度、正交平衡度、直流偏移、阻抗匹配以及本振泄漏等。如今，传统的模拟解调机制正在被数字化解调逐步代替，从而提高了系统的稳定性和信号分析的灵活性。图3-15是数字正交解调电路的一种基本模型，输入的模拟中频信号首先经过A/D转换，实现数字采样，其数据流分两路通过数字乘法器分别与本地数字振荡器（NCO）产生的cos分量和sin分量相乘，实现输入信号在频域的搬移，即载波频率为零，随后进入数字低通滤波器，并根据信号带宽进行抽取，得到同相分量I（in-phase）和正交分量Q（quadrature）两路基带信号，从而实现中频信号的下变频和两路正交基带信号的获得。上述过程可以用数学表达式的形式说明，A/D转换后的信号以正交形式表示：

其中，xI（n），xQ（n）分别为信号的同相分量和正交分量，ωc是输入中频信号的载波频率。

S（n）通过与数字振荡器信号相乘便可实现下变频：经过数字低通滤波器滤除二次谐波分量后即可得到期待的两路基带信号

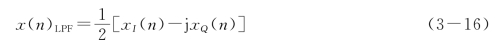
根据测量仪器不同的信号分析要求，输出结果由FPGA加上DSP做进一步的处理。由于数字本振、数字混频和数字滤波器的应用，电路的稳定性得到了很好的保证，通过改变数字本振的频率和相位、数字滤波器的通带特性，能够方便灵活地获得输入中频信号的幅度和相位特征，并且具有很好的一致性。