数字直接合成法：直接合成的另一种方式

前面两种信号合成方法都是基于频率合成的原理，通过对基准频率进行加、减、乘、除算术运算得到所需的输出频率。自20世纪70年代以来，由于大规模集成电路的发展，开创了另一种信号合成方法——直接数字合成法（Direct Digtal Frequency Synthesis，简写为DDFS或DDS）。它突破了前两种频率合成法的原理，从“相位”的概念出发进行频率合成。这种合成方法不仅可以给出不同频率的正弦波，而且还可以给出不同初始相位的正弦波及其他各种各样形状的波形。在前述两种合成方法中，后两个性能是无法实现的。由于DDS具有频带宽、频率转换速度快且相位连续、分辨率高、容易实现各种调制及扫频，以及工作稳定等优点，因而近十多年来得到了飞速发展。这里仅讨论正弦波的合成问题，关于任意波形将在后面进行讨论。

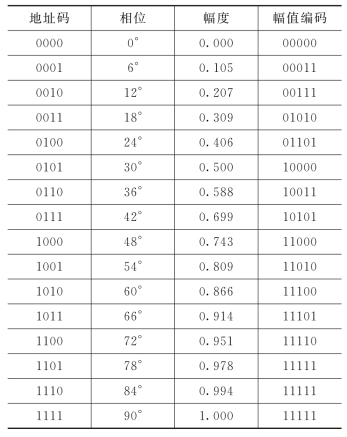
表2-1　正弦波信号相位-幅度关系

1）直接数字合成基本原理

由图2-9可见，直接数字合成的过程是在参考时钟CLK的作用下，相位累加器输出按一定间隔递增的地址码寻址ROM（或RAM），地址递增的间隔取决于频率控制字。在ROM内存放波形数据，因而称为正弦查阅表。被寻址的ROM单元中的数据被读出，再进行数模转换（D/A），就可以得到一定频率的输出波形。由于输出信号（在D/A的输出端）为阶梯状，为了使之成为理想正弦波还必须进行滤波，滤除其中的高频分量，所以在D/A之后接一平滑滤波器，最后输出频率为f0的正弦信号波形。

现以正弦波为例进一步叙述如下。在正弦波一周期（360°）内，按相位划分为若干等分（ΔΦ），将各相位所对应的幅值（A）按二进制编码并存入ROM。设相位间隔ΔΦ=6°，则一周期内共有60等分。由于正弦波对180°（为奇对称，对90°和270°为偶对称），因此ROM中只需存0°～90°范围的幅值码。若以ΔΦ=6°计算，在0°～90°之间共有15等分，其幅值在ROM中占16个地址单元。因为24=16，所以可以按4位地址码对数据ROM进行寻址。现设幅度码为5位，则在0°～90°范围内编码关系如表2-1所示。

2）信号的频率关系

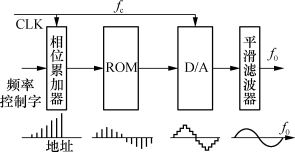
图2-9　直接数字合成原理框图

在图2-9中，时钟CLK的速率为固定值fc。在CLK的作用下，如果按照0000→0001→0010→…→1111的地址顺序读出ROM中的数据，即表2-1中的幅值编码，其输出正弦信号频率为f01；如果每隔一个地址读一次数据（即按0000→0010→0100→…→1110次序），其输出信号频率为f02；f02将比f01提高1倍，即f02=2f01，依此类推。这样，就可以实现直接数字频率合成器的输出频率的调节。

上述过程是由图2-10中的相位累加器实现的，由相位累加器的输出决定选择数据ROM的地址（即正弦波的相位）。输出信号波形的产生是相位逐渐累加的结果，因而称为相位累加器。图中4位寄存器的Q4～Q1输出作为ROM的当前地址码，同时送到4位加法器的B4～B1端与K值（送至A4～A1端）相加得∑4～∑1。后者送至寄存器的D4～D1端，在下一个CLK作用下打入寄存器，作为下一地址码。K为累加值，即相位步进码，又称频率控制字。如果K=1，每次累加结果的增量为1，则依次从每个数据ROM的单元中读取数据。如果K=2，则每隔一个ROM地址读一次数据，依此类推。因此K值越大，相位步进越快，输出信号的频率越高。

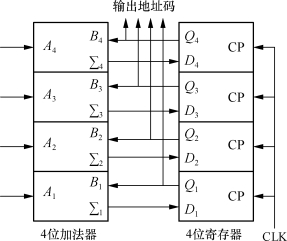
图2-10　相位累加器原理

在时钟（CLK）频率一定的情况下，输出的最高信号频率为多少？或者说在相应于n位地址的ROM范围内，最大的K值应为多少？对于n位地址来说，共有2n个ROM地址，在一个正弦波中有2n个样点（数据）。如果取K=2n，就意味着相位步进为2n，一个信号周期中只取一个样点，它不能表示一个正弦波，因此不能取K=2n；如果取K=2n-1，2n/2n-1=2，则一个正弦波形中只有两个样点，这在理论上满足了取样定理，但实际上是难以实现的。一般限制K的最大值为

这样，一个波形中至少有4个样点（2n/2n-2=4），经过D/A变换，相当于4级阶梯波，即图2-9中的D/A输出波形由4个不同的阶跃电平组成，在后继平滑滤波器的作用下，可以得到较好的正弦波输出。相应地，K为最小值（Kmin=1）时，一共有2n个数据组成一个正弦波。

根据以上讨论可以得到如下一些频率关系。假设时钟频率为fc，ROM地址码的位数为n。当K=Kmin=1时，输出频率f0为：

故最低输出频率f0min为：

故最高输出频率f0max为：

在DDS中输出频率点是离散的，当f0max和f0min已经设定时，其间可输出的频率个数M为

现在讨论DDS的频率分辨率。如前所述，频率分辨率是两个相邻频率之间的间隔，现在定义f1和f2为两个相邻的频率，若：

则：

(www.xing528.com)

因此，频率分辨率Δf为：

故得：

为了改变输出信号频率，除了调节累加器的K值以外还有一种方法，就是调节控制时钟的频率fc。由于fc不同读取一轮数据所花时间不同，因此信号频率也不同。用这种方法调节频率，输出信号的阶梯仍取决于ROM单元的多少，只要有足够的ROM空间都能输出逼近正弦的波形，但调节fc比较麻烦。

3）杂散分量和噪声分析

在DDS输出波形中所含的杂散分量和噪声主要有下列几种：镜像频率分量；模拟信号幅度的量化噪声；时间轴量化不均匀导致的相位噪声；D/A转换器性能误差导致的信号失真。下面分别讨论。

（1）采样信号的镜像频率分量

由图2-9可见，DDS合成的是正弦波的离散采样值的数字量经D/A转换成阶梯状的模拟波形，它与我们期望的单频正弦波是有差别的。实际上，DDS输出的是一个被取样的正弦信号。根据取样理论，未经滤波的DDS输出信号的频谱如图2-11所示。由图可见，DDS输出信号中除了要求的f0基频信号外，还有一系列镜像频率信号，其频率为（nfc±f0），n=1，2，3。整个频谱的幅度沿sin（πf0/fc）/（πf0/fc）包络滚降。最大的电压杂散信号出现在第一镜像频率（fc-f0）处。随着f0的增加，杂散信号将逐渐靠近输出频率。当f0=fc/2时f0将与第一镜像频率（fc-f0）重合在一起，因而无法用低通滤波器将（fc-f0）滤掉。为此，虽然在理论上DDS最高输出频率可达fc/2，实际上通常选择f0＜fc/3；这样能较好地滤除镜像频率，而低通滤波器的设计也不太困难。

图2-11　未滤波的DDS输出典型频谱

由图2-11可见，输出信号（f0）与最大杂散（fc-f0）的功率比（即信噪比）为：

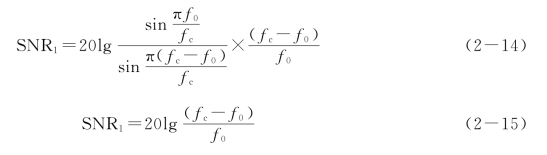
（2）幅度量化噪声

正弦查阅表内存储的波形码是一个模拟信号被均匀量化后的值。如果选用的DAC有D位，则模拟量在2D个离散区间内进行量化，由此造成的误差均匀地分布在-Δ/2～Δ/2之间。Δ=VFS/2D，VFS是DAC转换电压的满度值。

（3）相位噪声

为了得到高的频率分辨率，相位累加器的位数L一般取的比较大，例如L=32，这样，它能访问4 G（232）个存储器单元。但实际上ROM容量有限，不宜做这样大。因而就要从工位相位累加字中，截取高n位来寻址ROM，这就导致相位噪声。因为这时L分成两个部分L=n+B，高n位寻址ROM，低B位是被截掉的。当相位累加器在累加过程中，低B位的值RB小于2B（RB＜2B）时，则低B位向高n位无进位；当RB≥2B时，就要向高n位进1。若进l后的余数不为0，则下一次进位就会提前到来。经分析表明，这一误差序列是周期序列，其信噪比可用下式近似计算：

式中n为截取的位数，亦即ROM的地址码位数。

（4）D/A转换器非线性引起的杂散分量

D/A转换器的非线性转换特性会使它的输出电压V0产生失真，从而使DDS的输出信号频谱中增加杂散分量，这主要是f0的各次谐波分量。此外，由于分布电容等的影响，时钟fc亦会泄漏到D/A输出，造成杂散。时钟的相位噪声也会影响输出。

综合上述各种原因，表示了实际的DDS输出信号的频谱，其中除f0外，还包括由幅度及相位量化产生的噪声、镜像频率fc-nf0、f0的各次谐波泄漏及其他未知的杂散分量。

为了减小DDS输出电压中的杂散及噪声，应采取下列措施：

①设计良好的低通滤波器，以滤除各种杂散及带外噪声。

②选用性能优良的D/A转换器。

③减小f0/fc比例，可改善信号质量，一般选用f0/fc≤33%。

④适当提高D/A位数及正弦查询表的长度。D/A位数D与查询表ROM的地址线数n对信噪比的影响是基本相同的，而总的噪声是它们的合成，因此单独增加D或n没有实际意义，应使n=D或n=D+2，这就是所谓的对称性设计原则。

⑤谨慎排版、布线，以减小各种泄漏和干扰。