回转面与回转体的几何形态及投影方法

由一条母线(直线或曲线)围绕轴线回转而形成的表面被称为回转面； 由回转面或回转面与平面围成的立体被称为回转体。

圆柱、 圆锥、 球等都是回转体， 它们的画法和回转面的形成条件有关， 下面分别介绍。

画回转体的三视图时， 轴线的投影用细点画线绘制， 圆的中心线用相互垂直的细点画线绘制， 其交点为圆心。 所画的细点画线均应超出轮廓线3 ~5mm。

1. 圆柱体

(1)圆柱体的形成。 如图2-54(a)所示， 圆柱面可看作一条直线AB 围绕与它平行的轴线OO 回转而成。 OO 被称为回转轴， 直线AB 被称为母线， 母线转至任一位置均被称为素线。

圆柱体的表面是由圆柱面和上、 下底圆平面围成的。

(2)圆柱体的三视图。 如图2-54(b)所示为圆柱体的投射情况， 如图2-54(c)所示为圆柱体的三视图。 由于圆柱体的轴线为铅垂线， 圆柱面上的所有素线都是铅垂线，所以其水平投影积聚成一个圆。 圆柱体的上、 下两底圆均平行于水平面， 其水平投影反映实形， 为与圆柱面水平投影重合的圆平面。

主视图的矩形表示圆柱面的投影， 其上、 下两边分别为上、 下底面的积聚性投影；左、 右两边分别为圆柱面最左、 最右素线的投影， 这两条素线的水平投影积聚成两个点， 其侧面投影与轴线的侧面投影重合。 最左、 最右素线将圆柱面分为前、 后两半[见图2-54(b)]， 是圆柱面由前向后的转向线， 也是圆柱面在正面投影中可见与不可见部分的分界线。

图2-54　圆柱体及其三视图

(a)圆柱面的形成　(b)圆柱体的投射情况　(c)圆柱体的三视图

左视图的矩形线框可与主视图的矩形线框做类似的分析。

轴线为侧垂线的圆柱体投射情况及其三视图如图2-55 所示。

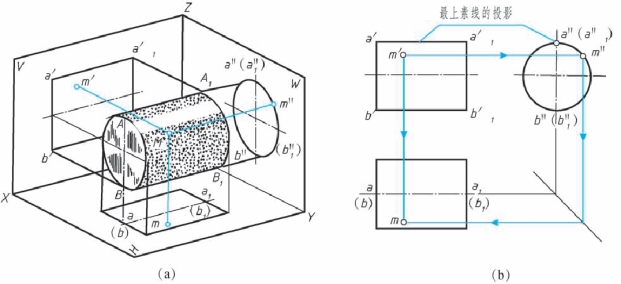
图2-55　圆柱体的三视图及其表面上的点

由此可总结出圆柱的形体特征: 圆柱由两个相等的圆底面和一个与其垂直的圆柱面围成； 其三视图的特征是: 一个视图为圆， 其他两个视图均为相等的矩形线框。

画圆柱体的三视图时， 先用细点画线画出轴线的投影和圆的两条中心线， 再画出圆柱面有积聚性的投影(圆)， 最后根据圆柱体的高度和投影规律画出其他两视图。

(3)圆柱体表面上的点。 如图2-55 所示， 已知圆柱面上点M 的正面投影m′， 求m和m″。

由于圆柱的轴线为侧垂线， 圆柱面的侧面投影积聚成一个圆， 点M 的侧面投影一定重影在圆周上。 据此， 作图时应先求出m″， 再由m′和m″求出m。 因点M 位于圆柱的上表面， 所以其水平投影m 为可见。

2. 圆锥体

(1)圆锥面的形成。 如图2-56(a)所示， 圆锥面可看作一条直母线SA 围绕和它相交的轴线OO 回转而成。 圆锥体的表面是由圆锥面和一个垂直于轴线的底圆平面围成的。

(2)圆锥体的三视图。 如图2-56(b)所示为圆锥体的投射情况， 如图2-56(c)所示为圆锥体的三视图。 由于圆锥体的轴线为铅垂线， 底面为水平面， 它的水平投影为一圆， 反映底面的实形， 同时也表示圆锥面的投影。

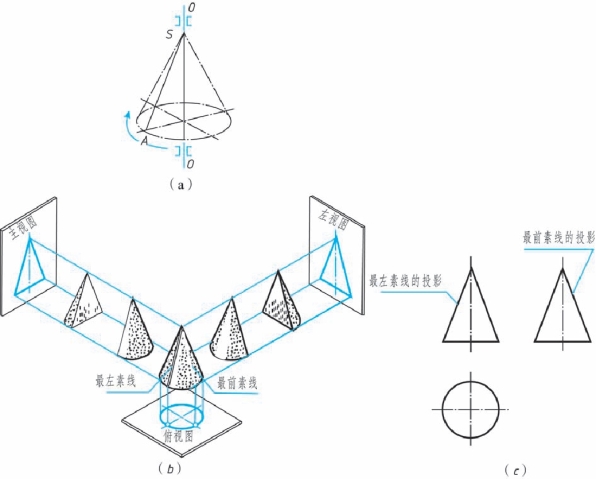
图2-56　圆锥体及其三视图

(a)圆锥面的形成　(b)圆锥体的投射情况　(c)圆锥体的三视图

主视图、 左视图均为等腰三角形， 其下边均为圆锥底面的积聚性投影。 主视图中三角形的左、 右两边， 分别表示圆锥面最左、 最右素线的投影(反映实长)； 左视图中三角形的两边， 分别表示圆锥面最前、 最后素线的投影(反映实长)， 也是圆锥面在侧面投影中可见与不可见部分的分界线。 上述四条线的其他两面投影与圆柱相类似。

由此可总结出圆锥的形体特征: 它由一个圆底面和一个锥顶位于与底面相垂直的中心轴线上的圆锥面围成； 其三视图的特征是: 一个视图为圆， 其他两个视图均为相等的等腰三角形。

画圆锥体的三视图时， 应先依次画出轴线的投影、 圆的中心线、 底圆及顶点的各投影， 再画出四条特殊位置素线的投影。

(3)圆锥体表面上的点。 如图2-57 所示， 已知圆锥体表面上点M 的正面投影m′，求m 和m″。 根据m′的位置和可见性， 可判定点M 在前、 左圆锥面上， 因此点M 的三面投影均为可见。

图2-57　圆锥体的三视图及表面上的点

作图时可采用以下两种方法。

①辅助素线法: 如图2-57(a)所示， 过锥顶S 和点M 作一辅助素线S1， 即在图2-57(b)中连接s′m′， 并延长到与底面的正面投影相交于1′， 求得s1 和s″1″； 再由m′根据点在线上的投影规律求出m 和m″。

②辅助圆法: 如图2-57(a)所示， 过点M 在圆锥面上作垂直于圆锥轴线的水平辅助圆， 该圆的正面投影积聚为一直线， 即过m′所作的2′3′ [见图2-57(c)]， 其水平投影为一直径等于2′3′的圆。 由于点M 的投影应在辅助圆的同面投影上， 所以即可由m′求得m， 再由m′和m 求得m″。(www.xing528.com)

圆锥体被平行于底面的平面截去其上部， 所剩的部分被称为圆锥台， 简称圆台。圆台及其三视图如图2-58 所示。

图2-58　圆台及其三视图

(a)方位一　(b)方位二　(c)方位三

由此可总结出圆台三视图的形体特征: 一个视图为两个同心圆， 其他两个视图均为相等的等腰梯形。

3. 球

(1)球面的形成。 如图2-59(a)所示， 球由球面围成。 球面可看作一圆母线围绕它的直径回转而成(球体的任何直径都可视为回转轴线)。

(2)球的三视图。 如图2-59(b)所示为球的投射情况， 如图2-59(c)所示为球的三视图。 它们都是与球直径相等的圆， 均表示球面的投影。 球的各个投影虽然都是圆，但各个圆的意义却不相同。 主视图中的圆是平行于V 面的圆素线Ⅰ(前、 后半球的分界线， 球面正面投影可见与不可见的分界线)的投影[见图2-59(b)(c)]； 按此做类似分析， 俯视图中的圆是平行于H 面的圆素线Ⅱ的投影； 左视图中的圆是平行于W 面的圆素线Ⅲ的投影。 这三条圆素线的其他两面投影都与圆的相应中心线重合。

图2-59　球及其三视图

(a)球面的形成　(b)球的投射情况　(c)球的三视图

(3)球表面上的点。 如图2-60(a)所示， 已知圆球面上点M 的水平投影m， 求其他两面投影。 根据m 的位置和可见性， 可判定点M 在前半球的左上部分， 因此点M 的三面投影均为可见。

图2-60　球的三视图及表面上的点

作图时应采用辅助圆法。 即过点M 在球面上作一平行于正面的辅助圆(也可作平行于水平面或侧面的圆)。 因点在辅助圆上， 故点的投影必在辅助圆的同面投影上。

作图时， 先在水平投影中过m 作ef/ /OX， ef 为辅助圆在水平投影面上的积聚性投影，再画正面投影为直径等于ef 的圆， 由m 作OX 轴的垂线， 其与辅助圆正面投影的交点(因m 可见， 应取上面的交点)即为m′， 再由m、 m′求得m″ [见图2-60(b)]。

4. 圆环

(1)圆环面的形成。 如图2-61(a)所示， 圆环由圆环面围成。 圆环面可看作由一圆母线绕一与圆平面共面但不通过圆心的轴线回转而成。

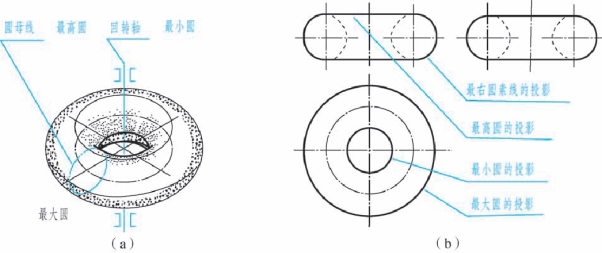
图2-61　圆环面的形成及其视图分析

(2)圆环的三视图。 如图2-61(b)所示: 主视图上的两个小圆是平行于V 面的两条圆素线的投影； 左视图上的两个小圆是平行于W 面的两条圆素线的投影: 俯视图中的两个实线圆分别是最大圆和最小圆的投影； 主、 左视图中两个小圆的上、 下公切线分别是圆环最高圆和最低圆的投影。

(3)圆环表面上的点如图2-62 所示， 已知圆环面上点M 的正面投影m′(可见)， 求其他两面投影。 根据m′的位置和可见性， 可判定点M 在外环面的左、 前、 上方， 所以水平投影m 应在左前方， 是可见的。 具体作图时， 可应用辅助圆法。

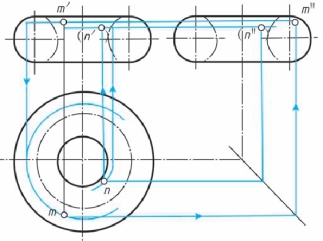
图2-62　圆环表面上的点

5. 不完整的回转体

几何体作为物体的组成部分不都是完整的， 也并非总是直立的。 多看、 多画些形体不完整、 方位多变的几何体及其三视图， 熟悉它们的形象， 对提高看图能力非常有益。 为此， 下面给出了多种形式的不完整回转体及其三视图(见图2-63、 图2-64)以做参考。

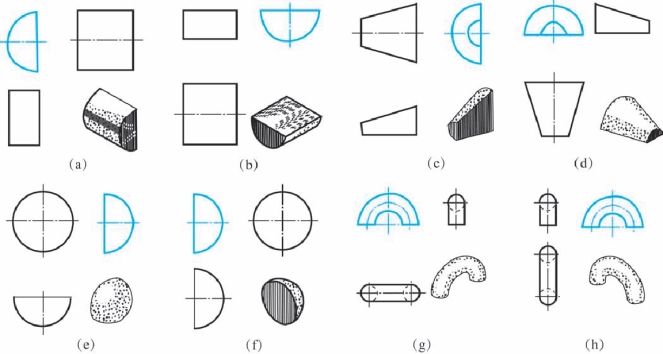
图2-63　二分之一回转体及其三视图

图2-64　四分之一回转体及其三视图

阅读时， 应先看具有特征形状的视图， 即先看具有圆(或其一部分)的视图， 再根据其他两视图的外形轮廓线， 分析它是哪种回转体， 属于哪一部分， 再将它归属于完整的回转体及其三视图的方位之中。 这样， 在整体形象的提示下进行局部想象， 往往会收到很好的效果。

值得一提的是， 在看物记图、 看图想物的过程中， 不应忽略图中的细点画线。 它往往是物体对称中心面、 回转体轴线的投影或圆的中心线， 在图形中起着基准或定位的作用。 弄清这个道理， 对画图、 看图、 标注尺寸等都很有帮助。