使用换面法计算直线长度和平面形状

1. 认识换面法

如图2-37 所示为一处于铅垂位置的三角形平面在V/H 体系中不反映实形， 现作一个与H 面垂直的新投影面V1 平行于三角形平面， 组成新的投影面体系V1/H， 再将三角形平面向V1 面进行投影， 这时三角形平面在V1 面上的投影就反映该平面的实形。 这种变换投影面使空间的直线或平面在新投影面上处于有利于解题(反映实长、 实形)的位置的方法称为换面法。

图2-37　换面法的原理

2. 点的投影变换

点是最基本的几何元素， 因此必须首先研究在变化投影面时， 点的投影变换规律。

(1)新投影面的选择。 在进行投影变换时， 新投影面是不能任意选择的， 首先要使空间几何元素在新投影面上的投影能够帮助我们更方便地解决问题。 并且新投影面必须要和不变的投影面构成一个直角两面体系， 这样才能应用正投影原理作出新的投影图来。 因而新投影面的选择必须符合以下两个基本条件。

①新投影面必须垂直于原投影面体系中的一个不变的投影面。

②新投影面必须使空间几何元素处于有利于解题的位置。

(2)点的一次换面。 根据选择新投影面的条件可知， 每次只能变换一个投影面。 变换一个投影面即能达到解题要求的称为一次换面。

①变换V 面， 即V/H→V1/H。 如图2-38 中a、 a′为点A 在V/H 体系中的投影， 在适当的位置设一个新投影面V1 代替V， 必须使V1⊥H， 从而组成了新的投影体系V1/H。V1 与H 的交线X1 为新的投影轴。 由A 向V1 作垂线得到新投影面上的投影a1′， 而水平投影仍为a。

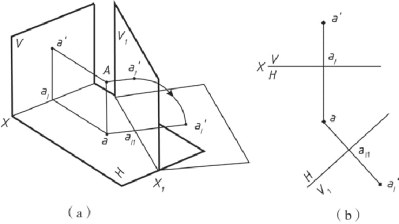
图2-38　变换V 面

②变换H 面， 即V/H→V/H1。 从图2-39 中看出， 用H1 代替H 组成新投影面体系V/H1， 由于V 面不变， 所以点到V 面的距离不变。 即a1ar1 ＝aar ＝y 坐标。

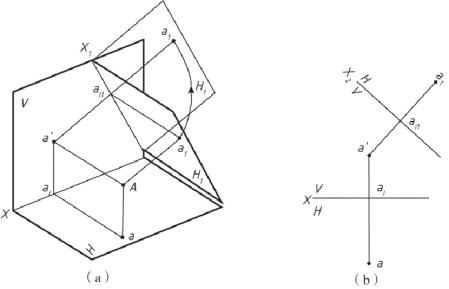
图2-39　变换H 面

(3)点的二次换面。 点的二次变换的原理和方法与第一次变换基本相同， 只是将作图过程重复一次， 但要注意新、 旧体系中坐标的量取， 其作图方法和步骤如图2-40所示。

图2-40　点的二次变换

注意: 新投影面的设置必须符合前述两个原则， 而且必须交替变换， 若第一次用V1 面代替V 面， 组成V1/H 新体系， 第二次变换则应用H2 面代替H 面组成V1/H2 体系，可如此交替多次变换达到解题目的。

3. 直线的投影变换

直线是由两点决定的， 因此当直线变换时， 只要将直线上任意两点的投影加以变换， 即可求得直线的新投影。

在解决实际问题时， 根据实际需要经常要将一般位置线变换成平行或垂直于新投影面的位置。

(1)直线的一次换面。

①将一般位置线变换为投影面平行线。 当一般位置线变换为投影面平行线时， 就可以求出线段的实长和对投影面的倾角。

如图2-41 所示， AB 为一般位置线， 如要变换为正平线， 则必须变换V 面， 使新投影面V1 面平行AB， 这样AB 在V1 面上的投影a1′b1′将反映AB 的实长， a1′b1′　与X1 轴的夹角反映直线对H 面的倾角α。

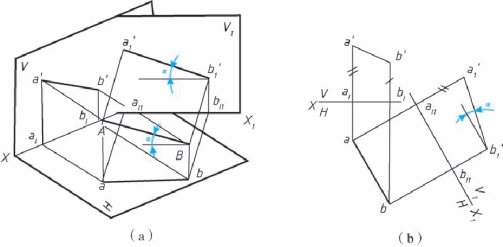
图2-41　一般位置线变换为投影面平行线(求α 角)

②将投影面平行线变换为投影面垂直线。 如图2-42 所示， 将正平线AB 变换为垂直线。 根据投影面垂直线的投影特性， 反映实长的投影必定为不变投影， 只要变换水平投影面， 即作新投影面H1 面垂直AB， 这样AB 在H1 面上的投影重影为一点。(www.xing528.com)

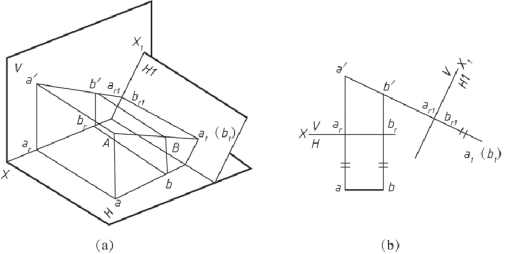
图2-42　正平线变换为投影面垂直线

在图中， 如果要求将水平线AB 变换为垂直线， 只要变换正投影面， 即作新投影面V1 面垂直AB， 这样AB 在V1 面上的投影重影为一点， 如图2-43 所示。

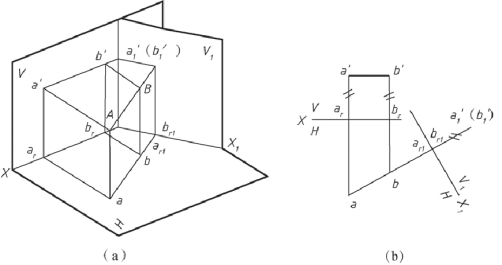
图2-43　水平线变换为投影面垂直线

(2)直线的二次换面。 直线的二次换面可以将一般位置线变换为投影面垂直线。 第一次将一般位置线变换为投影面平行线， 第二次将投影面平行线变换为投影面垂直线。

如图2-44 所示， AB 为一般位置线， 如先变换V 面， 使V1 面平行AB， 则AB 在V1/H 体系中为投影面平行线， 再变换H 面， 作H2 面垂直AB， 则AB 在V1/H2 体系中为投影面垂直线。

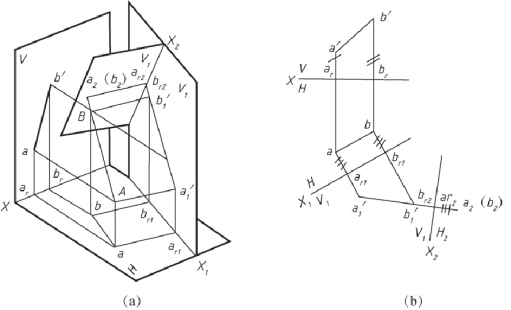
图2-44　一般位置线变换为投影面垂直线

4. 平面的投影变换

平面的投影变换， 就是将决定平面的一组几何要素的投影加以变换， 从而求得平面的新投影。 根据具体要求， 可以将平面变换成平行或垂直于新投影面的位置。

(1)平面的一次换面。

①将一般位置面变换为投影面垂直面。 当一般位置面变换为投影面垂直面时， 就可以求出平面对投影面的倾角。

如图2-45 所示， △ABC 为一般位置面， 如要变换为正垂面， 则必须取新投影面V1代替V 面， V1 面既垂直于△ABC， 又垂直于H 面， 为此可在三角形上先作一水平线，然后作V1 面与该水平线垂直， 则它也一定垂直H 面。

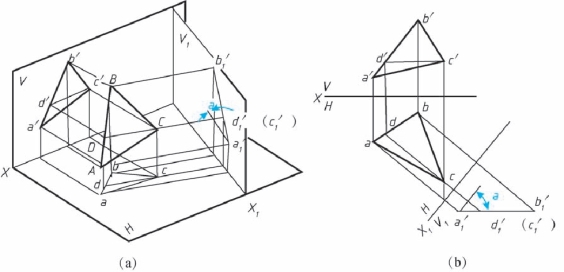
图2-45　一般位置平面变换为投影面垂直面(求α 角)

在图中， 如果要求△ABC 对V 面的倾角β， 可在此三角形平面上先作一正平线AE，然后作H1 面垂直AE， 则△ABC 在H1 面上的投影为一直线， 它与X1 轴的夹角反映△ABC 对V 面的倾角β， 如图2-46 所示。

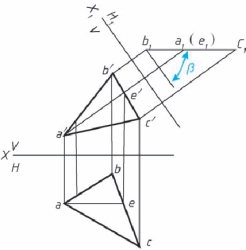
图2-46　一般位置平面求β 角

②将投影面垂直面变换为投影面平行面。 如图2-47 所示为铅垂面△ABC， 要求变换为投影面平行面。 根据投影面平行面的投影特性， 重影为一直线的投影必定为不变投影， 因此可以变换V 面， 使新投影面V1 平行△ABC， 这样△ABC 在V1 面上的投影△a1′b1′c1′反映实形。

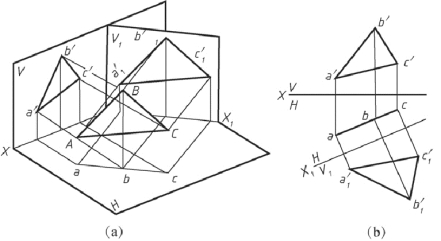
图2-47　垂直面变换为平行面

(2)平面的二次换面。

平面的二次换面可以将一般位置面变换为投影面平行面。 第一次将一般位置面变换为投影面垂直面， 第二次将投影面垂直面变换为投影面平行面。

如图2-48(a)所示为△ABC 为一般位置面， 为了求出它的实形， 必须变换两次， 先将△ABC 变换为垂直面， 再变换为平行面。

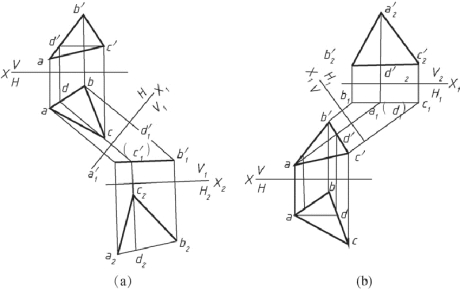
图2-48　一般位置面变换为投影面垂直面

同理， 也可以先变换H 面， 在此基础上再变换一次V 面， 如图2-48(b)所示，△a2′b2′c2′为所求实形。