点的三面投影如何绘制？

点的投影

点是最基本的几何要素。 为了迅速而正确地画出物体的三视图，首先必须掌握点的投影规律。 例如图2-11(b)所示的正三棱锥， 由△SAB、 △SBC、 △SAC 和△ABC 四个棱面组成， 各棱面分别交于校线SA、 SB……各校线分别汇交于顶点A、 B、 C、 S。 显然， 绘制三棱锥的三视图， 实质上就是画出这些顶点的三面投影， 然后依次连线而成， 如图 2-11(a)所示。

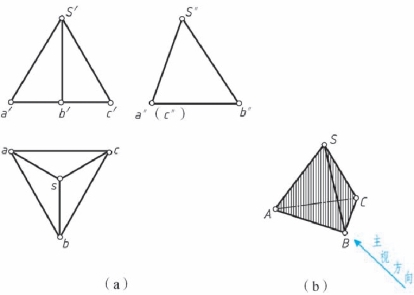
图2-11　物体上点的投影分析示例

1. 点的投影规律

如图2-12(a)所示， 求点S 的三面投影， 就是由点S 分别向三个投影面作垂线， 其垂足s、 s′、 s″即为点S 的三面投影图^[1]。 移去空间点S， 将H、 W 面按箭头所指的方向[见图2-12(b)] 旋转至与V 面在同一个平面上、 便得到点S 的三面投影图[见图2-12(c)]。 图中sx、 syH、 syW、 sz 分别为点的投影连线与投影轴OX、 OY、 OZ 的交点。

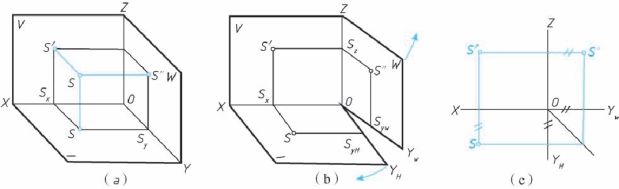
图2-12　点的三面投影

通过点的三面投影图的形成过程， 可总结出点的投影规律。

(1)点的两面投影的连线必定垂直于相应的投影轴。 即: ss′⊥OX、 s′s″⊥OZ、 ssyH⊥OYH、 s″syW⊥OYW。

(2)点的投影到投影轴的距离， 等于空间点到相应的投影面的距离， 即“影轴距等于点面距”。

s′sx ＝s″sy ＝Ss(点S 到H 面的距离)；

ssx ＝s″sz ＝Ss′(点S 到V 而的距离)；

ssy ＝s′sz ＝Ss″(点S 到W 面的距离)。

2. 点的投影与直角坐标的关系

点的空间位置可用直角坐标来表示， 即把投影面当作坐标面， 投影轴当作坐标轴， 三个轴的交点O 即为坐标原点。 从图2-13(a)可以看出，空间点S 到W 面的距离Ss″平行且等于OX 轴上的线段Osx。 把Osx 称为点S 的X 坐标， 并以x 表示。 对其他两个方向做类似的推导， 即可得出点的坐标与点到投影面距离的关系[见图2-13(b)]:

点的投影与直角坐标的关系

图2-13　点的投影与直角坐标的关系

x ＝Osx ＝Ss″(点S 到W 面的距离)；

y ＝Osy ＝Ss′(点S 到V 面的距离)；

z＝Osy ＝Ss(点S 到H 面的距离)。

由此可见， 点的投影与其坐标是一一对应的。 因此， 可以直接从点的投影图中量得点的各向坐标， 或根据点的投影确定点的空间位置。 反之， 根据点的坐标可以直接判定点的空间位置， 并画出其点的三面投影图。

【例2-1】 已知点A 的两面投影和点B 的坐标为(25， 20， 30)， 求点A 的第三面投影及点B 的三面投影[见图2-14(a)]。

解: (1)求A 点的侧面投影。 先过原点O 作45°辅助线。 过a 作∥OX 轴的直线与45°辅助线相交于一点， 过交点作⊥OYW 的直线， 该直线与过a′平行于OX 轴的直线相交于一点即为所求侧面投影a″。

(2)求B 点的三面投影。 在OX 轴取ObX ＝25mm， 得点bX， 过bX 作OX 轴的垂线，取b′bX ＝30mm， 得点b′， 取bbX ＝20mm， 得点b； 同求A 点的侧面投影一样， 可求得点B 的侧面投影b″。 答案见图2-14(b)。

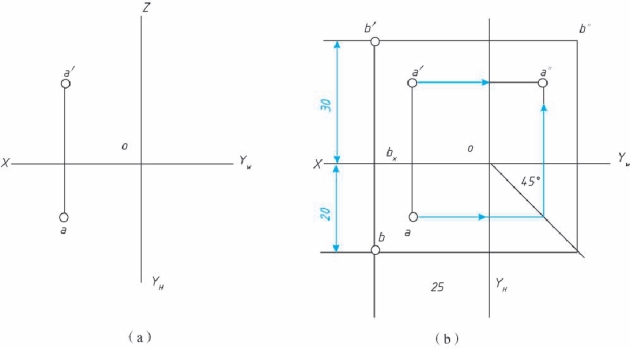
图2-14　求作点的投影

3. 两点的相对位置

两点在空间的相对位置可以由两点的三向坐标差来确定， 如图2-15 所示。

(www.xing528.com)

图2-15　两点的相对位置

两点的左、 右位置由X 坐标差确定， X 坐标值大者在左， 故点A 在点B 的左方；

两点的前、 后位置由Y 坐标差确定， Y 坐标值大者在前， 故点A 在点B 的后方；

两点的上、 下位置由Z 坐标差确定， Z 坐标值大者在上， 故点A 在点B 的下方。

在图2-16 所示E、 F 两点的投影中， e′和f′重合， 这说明E、 F 两点的X、 Z 坐标相同， 即E、 F 两点处于对立面的同一条投射线上。

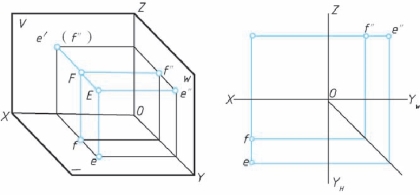
图2-16　利用两点不重影的坐标大小判别重影点的可见性

可见， 共处于同一条投射线上的两点， 必在相应的投影面上具有重合的投影。 这两个点被称为对该投影面的一对重影点。

重影点的可见性需根据这两点不重影的投影的坐标大小来判别。

对V 面， “前遮后”； 对H 面， “上遮下”； 对W 面， “左遮右”。

对不可见的点需加圆括号表示、 如图2-16 中点F 的V 面投影不可见， 加圆括号表示为(f′)。

4. 读点的投影图

从最基本的几何元素(点)开始讨论读图问题， 有利于培养正确的读图思维方式，从而为识读体的投影图打好基础。

【例2-2】 识读A、 B 两点的三面投影图[见图2-17(a)]。

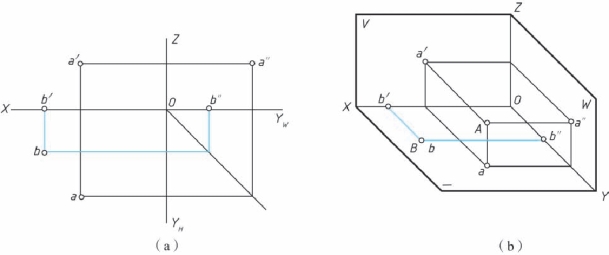
图2-17　识读A、 B 两点的投影图

(a)A、 B 两点的投影图　(b)A、 B 两点的空间位置

分析: 读两点的投影图， 首先应分析每个点的空间位置， 再根据其坐标确定两点的相对位置。

解: 从图中可见， 点B 的V、 W 面投影b′、 b″分别在OX、 OYW 轴上， 说明点B 的Z 坐标为0， 点B 在H 面上， 水平投影b 与其重合(点A 的分析从略)。

判别A、 B 两点的空间位置:

左、 右相对位置: xB－xA ＝7mm、 故点A 在点B 右方7mm；

前、 后相对位置∶yA－yB ＝9mm、 故点A 在点B 前方9mm；

上、 下相对位置: zA－zB ＝9mm， 故点A 在点B 上方9mm。

即点A 在点B 的右方7mm、 前方和上方各9mm 处。

至此， 看图的任务似乎已经完成。 其实不然， 还应在此基础上， 通过“想象” 建立起空间概念， 即在脑海中呈现出如图2-17(b)所示的立体状态， 这样才算真正将图看懂。

【例2-3】 以识读点A 的投影图[见图2-18(a)] 为例， 说明“想象” 点A 空间位置的过程， 具体如图2-18(b)(c)所示。

图2-18　根据投影图， 想象空间点位置的过程

(a)读点A 的三面投影图　(b)将H、 W 面转回90°， 使其与V 面垂直(c)过a′、 a、 a″分别作V、 H、 W 面的垂线， 交点即为点A 的空间位置

解: 因为图2-18(b)(c)这种图比较难画， 所以通常可以用简化的轴测图(画法如图2-19 所示)代替， 其直观效果与图2-18(b)(c)是一样的。

图2-19　作点的轴测图的步骤

(a)画轴测轴OX、 OY、 OZ　(b)画投影面， 在轴上取点的坐标　(c)作点A 的三面投影(d)过a′、 a、 a″分别作V、 H、 W 面的垂线， 交点即为点A 的轴测图