深入探究井巷工程仿真技术

通过对井巷工程的各种模型分析，井巷工程的仿真信息包括两部分内容：一部分是巷道底部中心线的属性信息，一般为起点坐标与终点坐标；另一部分是巷道断面的参数信息。由于断面类型（主要包括矩形、梯形和拱形3类）的不同，其巷道参数信息也各不相同，故需进一步求解断面各关键点的信息，从而形成适合面绘制技术的模型。在此，按照求解过程将井巷工程面绘制过程分解为3个部分：一是对巷道底部各点求解；二是对断面各关键点求解；三是利用三角面片、矩形面片或圆筒面片构建巷道的仿真模型。

1.巷道底边各点求解

所有类型的巷道均以直巷道形式存储，其存储方式为底部中心线的起点和终点以及断面形状。为了表现巷道整体形态，故须由底部中心线和断面宽度信息求解巷道底部的各点坐标值。对于水平巷道底部的形状，在平面上可以视为一个规则的矩形结构；对于斜巷道底部的形状，通过向水平投影，同样可以视为一个矩形结构。所以，对巷道底部各点坐标值的求解，就可以转换为求矩形各点的坐标值。

设巷道底部的中心线为AB，巷道宽度为width，则其底部矩形为A1B1B2A2，见图4.12（a）。若直接求A1、A2、B1、B2各点，则需考虑很多种特殊情况，如中心线AB所在象限的不同引起的求解不同等情况，故采用平移和坐标变换的方法对中心线AB进行修改，将中心线AB限定某一具体象限中。其具体方法如下。

（1）判断A点与B点的位置关系，并调整A、B点以保证XA＜XB，即若XA＞XB，互换A点B点。

（2）平移坐标，将A点作为原点，计算B点在新坐标系X′O′Y′中的相对位置，若YB＜0则在平移后中心线AB在第四象限中，YB＞0则在平移后中心线AB在第一象限，如图4.12（b）所示。

通过上述过程，就可以按以下5种情况确定A1、A2点所在象限。

（1）若YB＞0且XB≠0，因A1A2线与AB线垂直，且这两点关于O′点对称，故即A1点在第二象限，而A2点在第四象限。

（2）若YB＜0且XB≠0，则A1点在第一象限，而A2在第三象限。

（3）若YB＞0且XB=0，则A1点在X负坐标轴上，而A2在X正坐标轴上。

（4）若YB＜0且XB=0，则A1点在X正坐标轴上，而A2在X负坐标轴上。

（5）若YB=0，则A1点在Y正坐标轴上，而A2在Y负坐标轴上。

图4.12　巷道底部关键点求解示意图

现以A1点为例，如图4.12（c）所示，进行坐标的求解。由于将A点作为原点就可以将AB的直线方程式（4.8）简化为式（4.9）。

根据B点坐标可由式（4.10）求出AB斜率k，又因A1B1与AB平行，所以A1B1斜率也应为k，且A1B1到AB的距离为width/2，故A1到原点A应满足圆形方程式（4.11），求解二元二次方程组（4.12）。

根据解与系数的关系，方程组应存在两组解如式（4.13），由于此前对A1、A2点所在象限已经讨论，故可以快速地确定点A1坐标、A2坐标

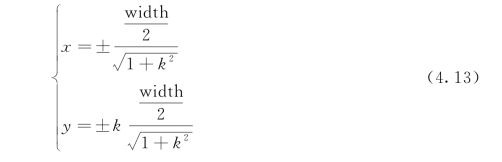(www.xing528.com)

同时，由于A1点、A点的关系与B1点与B点的关系类似，故可通过式（4.14）进行求解。

同理，根据A2点与A点的关系，以及B点坐标可求出B2点坐标。对于各点的Z坐标则以两端点的Z坐标为准，即至此，巷道底部矩形的各顶点坐标均已求出。

2.巷道断面各关键点求解

巷道的断面有很多种，但大体上可分为矩形、梯形和拱形等3种断面，如图4.13所示。在此，按照这3种断面将求解方法也分为矩形断面求解方法、梯形断面求解方法和拱形断面求解方法3类。

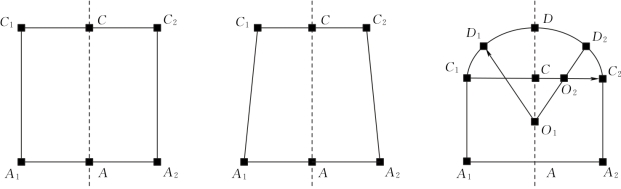
图4.13　断面类型

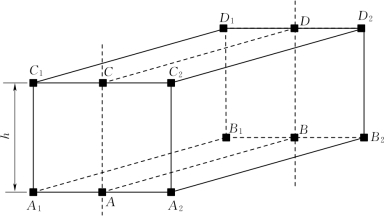
图4.14　矩形巷道示意图

（1）矩形断面求解方法。对于矩形断面的求解，如图4.14所示，已知巷道高度h和底部矩形的4个顶点的坐标，则顶部矩形的4个顶点C1、D1、D2、C2的坐标可分别由A1、B1、B2、A2点的坐标变换得出，即相对应点的X、Y坐标不变，Z坐标增加h。

（2）梯形断面求解方法。对于梯形断面的求解，如图4.15所示，若已知巷道高度h和底部矩形的4个顶点的坐标，及梯形断面的角度α，则可通过三角函数求出C1、C2点到中心C点的距离和D1、D2点到中心D点的距离，又因为C点、D点坐标可由A点、B点坐标求出，即相对应点的X、Y坐标不变，Z坐标增加h。故可以求解巷道底边各点的方式，求出巷道顶部矩形的4个顶点C1、D1、D2、C2的坐标。若已知w2，则可直接采用求解巷道底边各点的方式，求出巷道顶部矩形的坐标。

图4.15　梯形巷道示意图

（3）拱形断面求解方法。以三心拱为例求解拱形断面各关键点，如图4.16所示，已知巷道的底部矩形的4个顶点的坐标、高跨比f、宽度w和巷道高度，可求得高度h1、拱高h2以及C、C1、C2、E、E1、E2、D、F各点坐标；又知三心拱的大弧半径R和小弧半径r，就可求得O1、O2点的坐标值；进而利用α角或β角求出D1、D2、F1、F2各点的坐标。

图4.16　拱形巷道示意图

3.巷道面绘制

就巷道的表现内容而言，通常所关注的是各种井筒、巷道、硐室、地下车场等的空间位置、形体及互关系等内容，这些内容可通过井巷所知的参数和属性信息构建面模型，并以面绘制方式进行展现。

对于矩形和梯形断面巷道，由于已知其模型的各顶点坐标，可以方便地采用矩形或三角形面片方式进行表示；而就拱形断面巷道而言，其侧壁及底部可采用矩形或三角形面片形成进行表达，对于顶部拱形结构在精度要求不高的情况下，可直接采用三角网连接各顶点进行绘制，对于要求仿真效果要求较高的情况，如需进行虚拟漫游时，则应采用以直代曲的方式，将弧形分解为更小的直线，用这些直线去逼近弧线，再以三角网去逼近拱形结构。