如何用MC法构造矿体模型？

在对矿体数据进行预处理和体素化后，矿体信息可被处理为以体素为基本单元的实体集合，并通过对体素空间所标识的属性将矿体实体与其他实体对象划分开。另外，MC法作为等值面构造模型可以方便地对指定品位的矿体进行面绘制，以表达相应品位条件下的矿体三维形态[160]。

1.矿体仿真的主要步骤

在矿体一体化模型的基础上，以体素作为最基本的处理单元，在每一个体素内构造三角面片作为等值面来逼近表示矿体表面，实现矿体表面的三维重建。在此，采用MC法进行三角面片的产生和矿体形状的三维可视化仿真。

（1）体素中等值面剖分方式的确定。确定体素中等值面的分布是MC法的基础。在体素空间中，体素可以用由空间数据场中的8个相邻点来表示。MC法的基本假设是沿着体素的棱边，数据场呈连续线性变化，也就是说，如果一条边的两个顶点分别大于、小于等值面的值，则在该边上必有也仅有一点是这条边与等值面的交点。根据这一原理就可以判断出所求等值面将与哪些体素相交，或者说将穿过哪些体素。

为了确定体素中等值面的剖分方式，首先给出所求等值面的一个阈值C（对于矿体而言，C表示矿体品位值），然后对体素的8个顶点进行分类，以判定其顶点是位于等值面之内还是位于等值面之外。再根据顶点分类的结果，确定等值面的剖分模式，如图4.2所示。顶点分类规则如下。

图4.2　体素中等值面位置的确定

1）如果顶点的数据值f≥等值面的阈值C，则定义该顶点位于等值面之内，标记为“1”。

2）如果顶点的数据值f＜等值面的阈值C，则定义该顶点位于等值面之外，标记为“0”。

由于每个体素有8个顶点，每个顶点可能有0或1两种状态，因此每个体素按其顶点的0、1分布而言，共有28=256种不同的构型。尽管判断等值面将与哪些体元相交在原理上很容易理解，但是根据这256种情况求出每个体素中的等值面却相当繁琐，也容易出错。

可利用对称性将这256种构型简化为15种。首先，利用互补对称性，将体素8个顶点的标记置反（0变为1、1变为0）。此时，等值面与体素中8个顶点之间的拓扑关系不会改变，亦即生成的等值面是相同的，这样可以将256种构型简化为128种。其次，根据旋转对称性可以将不同情况的种类进一步组合，可以将128种构型简化成15种。图4.3给出了这15种基本构型的三角剖分，它们反映了一个体素中8个顶点可能存在的全部256种状态。

图4.3　体素中等值面的15种基本构型

基于以上分析，MC法用一个字节的空间构造了一个体素状态表。如图4.4所示，该状态表中的每一位可表示该体素中一个顶点的0或1状态。根据这一状态表，就可以知道当前体素属于图4.3中的哪一种情况，以及等值面将与哪一条边相交。在Lorensen的处理中，首先建立一个“构型—三角剖分”查找表（图4.5），它包含256个索引项，每个索引项包含索引、旋转以及指向15种三角剖分中的一种指针。其中，索引（Index）是体素8个角点标记的有序二进制编码，即图4.4所示的体素状态表。对于每个体素，首先根据它的索引在“构型—三角剖分”查找表确定其三角剖分形式，然后再根据相应索引项中的旋转参数确定最终的三角剖分。

（2）求等值面与体元边界的交点。在确定体元内三角片的构成后，利用线性插值计算三角片顶点位置。对于矿体体素的某棱边，如果它的两个端点v1、v2标记不同，那么等值面一定与此棱边相交。

1）若体元棱边与x轴平行时，设该边的两端点为v1（i，j，k）、v2（i+1，j，k），则交点为v（x，j，k），x值的计算公式为

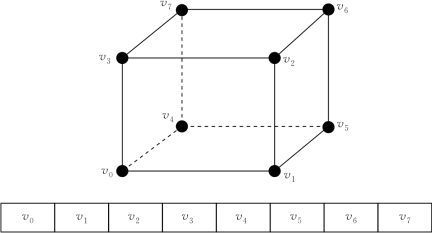
图4.4　体素角点函数值分布状态表

图4.5　构型—三角剖分结构

2）若体元棱边与y轴平行时，设该边的两端点为v1（

i，j，k）、v2（i，j+1，k），则交点为v（i，y，k），y值的计算公式为

3）若体元棱边与z轴平行时，设该边的两端点为v1（i，j，k）、v2（i，j，k+1），则交点为v（i，j，z），z值的计算公式为

利用上述公式，求得等值面与体元棱边的交点之后，根据数组索引确定三角片的构成，即可将这些交点连接成三角片，得到该体素内的等值面片。

（3）等值面的法向量计算。除了三角面片的生成，MC法还必须解决显示中表面法向量的计算问题。在确定了形成等值面的各三角面片的法向量之后，就可以选择适当的光照模型进行光照计算，生成真实感图形。

对于等值面上的每一点，其沿面的切线方向的梯度分量是零。因此，该点的梯度矢量的方向也就代表了等值面在该点的法向。MC方法就是利用这一原理来决定三角面片法向的，并且等值面往往是两种具有不同密度的物质的分界面，因而其梯度矢量不为零值，即

直接计算三角面片的法向是比较费时的，而且为了消除各三角面片之间明暗度的不连续变化，只要给出三角面片各顶点处的法向并采用哥罗德模型绘制各三角面片即可。

三角面片顶点的梯度也是通过所在棱边的两个端点的梯度经过线性插值得到。对于体元各角点处的梯度有不同的计算方法，但原理和效果基本类似。例如，可以采用中心差分计算各角点处的梯度，再利用线性插值求出三角面片各顶点的梯度，也就是各顶点处的法向，从而实现等值面的绘制。体元角上各点的中心差分计算公式为

(www.xing528.com)

式中：Δx、Δy、Δz分别是体元的边长。

2.MC算法实现过程

在MC法的算法实现过程中，须事先计算或读入具有256个元素的MC体元三角面片分布数组，然后按以下7步进行处理。

（1）将三维离散规则数据场分层读入。

（2）扫描两层数据，逐个构造体元，每个体元中的8个角上顶点取自相邻的两层。

（3）对每个体元，将体素中每个角上点的函数值与给定的品位值C做比较，以构造该体元的索引。

（4）根据索引在上面建立的256个元素的数组中查得该体元三角面片的分布情况。

（5）通过线性插值方法计算出该体元棱边与等值面的交点。

（6）利用差分方法（如上面介绍的中心差分方法），求出这个体元各角点处的法向量，再通过线性插值方法，求出三角面片各顶点处的法向。

（7）根据各三角面片各顶点的坐标、法向量绘制三角形，从而得到等品位值的三维矿体的面元模型。

3.MC算法二义性的排除

在上述由Lorenson提出的原始MC算法中，存在着构造三角面片的二义性问题，这一问题最早由M.I.Durst在1988年发现。

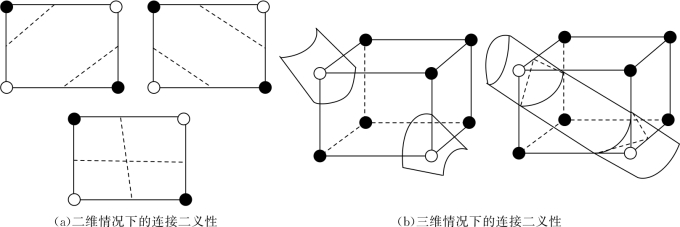
图4.6　等值面连接的二义性

在Lorenson的算法中，三角面片是根据等值面与体元棱边的交点确定的。但实际上，仅仅依靠交点，三角形的构造并不唯一，原因是在体元各个表面上的连线不唯一。通常情况下，等值面与体元的一个表面上的棱边的交点只有一对，这时在这个表面上只能产生一条用于构造三角面片的线段，也就是说，在这个面上，三角形的连接方式是确定的。但在图4.6中，等值面与体元的一个表面上的棱边的交点却有两对，能产生两条用于构造三角面片的线段，而且有两种连接这两条线段的方式，导致三角面片的结构不唯一。这样的面称为二义性面，包含一个以上的二义性面的体元即为具有二义性的体元。在图4.3中的15种构型中，第3、6、7、10、12、13种构型是具有二义性的。

当两个体元以一个二义性面作为它们的公共面时，如果这两个体元上的三角剖分导致它们的公共面具有不同的拓扑结构，那么就出现了拓扑不一致，这样就导致了所构造的等值面上出现孔隙的现象，显然这是不允许的。图4.7就是这样的一个例子。

图4.7　相邻立方体边界面上连接方式不一致而形成孔隙

目前，人们对该算法进行了不同的改进，以消除等值面构造的二义性。解决二义性的方法主要有以下几种。

（1）二义面平均值判定法（Facial Average Values）。计算二义面上4个顶点值的平均值，比较该平均值与阀值C的大小，并根据平均值大于或小于C分别选择可能的拓扑流形中的一种。

（2）子构型查找表（Subcase Table）。对于15种基本构型中的那些具有二义性的构型，各自建立一个子查找表，每个子查找表包含两种三角剖分方式。此外，还需存储一个表来记录这些三角剖分方式的相容性。

（3）梯度一致性准则（Gradient Consistency Heuristics）。由二义面上的4个角点梯度的平均值估算二义面中心点上的梯度，并根据该梯度方向决定二义面的拓扑流形。

（4）渐近线判别法（Asymptotic Decider）。该方法是由Nielson等人提出的最为常用的一种消除二义性的方法。

在一般情况下，等值面与体素边界面所在平面的交线是双曲线。该双曲线的两支及其渐近线与体素的一个边界的相互位置关系可用图4.8来表示。在该图所列的4种状态中，当双曲线的两支均与某边界面相交时，就产生了连接方式的二义性。此时，双曲线的两支将边界面划分为3个区域。可见，双曲线中两条渐近线的交点必然与边界面中位于对角线上的一对角点落在同一个区域内。

图4.8　双曲线与体素边界面的相互位置关系

式（4.7）所表示的双曲线的两条渐近线的交点坐标为

当出现二义性时，需要计算f（x，y，z0）的值。如果f（x，y，z0）＞C0，则渐近线的交点应与其函数值大于C0的一对角点落在同一区域内。如果f（x，y，z0）＜C0，则渐近线的交点应与其函数值小于C0的一对角点落在同一区域内。这就是当出现二义性时，交点之间的连接准则，如图4.9所示。在图中，当f（x，y，z0）＞C0时，对渐近线的交点标以正值，其对应的二义面称为正值二义面。当f（x，y，z0）＜C0时，对渐近线的交点标以负值，其对应的二义面称为负值二义面。

图4.9　出现二义性时交点之间的连接准则

在图4.3所列出的全部15种构型中，第0、1、2、4、5、8、9、11、14种不存在二义性面，因而它们只存在一种连接方式。第3、6种构型，各存在一个二义性面，因此各有两种不同的连接方式。第10、12种构型各存在两个二义性面，因而各有4种不同的连接方式。第7种构型存在3个二义性面，因而有8种不同的连接方式。第13种构型存在6个二义性面，因而有64种不同的连接方式。将以上各种情况加在一起，共有93种不同的连接方式，除去对称的和相同的方式，共有34种不同的连接方式。对于存在二义性的体素，按上述方法解决二义性问题，虽然增加了计算工作量，但是为了得出正确的结果却是十分必要的。