一体化构模方法优化指南

1.混合模型构造

构造三维实体模型的常用方法有边界描述法（Boundary Representation，Brep）、构造实体几何法（Constructive Solid Geometry，CSG）和混合法3种[157]。其中，Brep所构造的模型是由小平面或多边形构成表面，虽然可以较容易地建立不同的形状、曲线或复杂的模型，但其算法仅考虑对象的边界，没有考虑实体内部信息；而CSG造型则是通过一些基本简单实体如立方体、平行六面体、柱体、球体等来组合在一起构造复杂实体，由于这些简单对象的每一种也是一个实体，所以对复杂实体的内部特征的描述更加完备；混合法是混合采用Brep造型和CSG造型方法，共同构造三维实体模型。

出于矿山复合场仿真对象的范围及特点考虑，既有对如地表地形、断层等曲面的描述，又存在对矿体、巷道等实体的描述，故采用基于场量的混合构模方法进行实体构模。

对于Brep造型，也可采用场量作为基本构造单位，然后通过适当的组织和计算，以面片形式代替体元进行三维实体的造型。

对于CSG造型，一般是通过实体间的逻辑运算实现的，而这种逻辑运算常常产生实际上不存在的对象，如图3.1所示，实体A与实体B采用交运算而产生的悬面。通过分析可知，这种现象的产生主要是源于对所构造后实体边界的划分不确定所造成的，即在边界上的对象（悬面）既属于实体A又属于实体B，故逻辑运算后会产生实际上并不存在的对象。针对这一问题，在基于场量的矿山复合场模型构造的过程中，为使实体造型的过程满足一体化模型构模过程的需要，对研究区域中场量的基本性质和划分规则作出了两个基本规定。

（1）场量的基本性质。场量中的场元是最小实体单元，即具有不可再分性；同时，场元具有确定性，即一旦场元所属对象确定，并且场量中的场强和场向具有均质性，即它所代表的属性值唯一。

（2）对象空间划分规则。在三维对象的轮廓边界中，若存在某个场元被多个对象共同占有，则以几何体积所占比例最大的对象作为该场元所属对象。

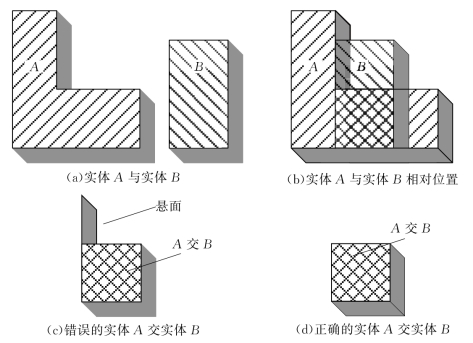
图3.1　CSG造型中逻辑运算产生的悬面

在这两个规定的基础上，针对某一对象的混合模型，均可按照面向对象的原则把其组织结构划分为场量、场量集合、实体类和仿真对象等4部分。

（1）场量。它是系统空间的最小组成单元，以一个三维数组作为组织结构。

（2）场量集合。它是在对三维空间进行规则划分后由一系列场量所构成的集合，该集合通过所包含的场元体现仿真对象的几何形体状态，是构造实体的基本组成结构，由于场量具有时效性，故其数据结构为一个场量的动态集合。

（3）实体类。由多个场量集合进行运算后所构成的单个仿真对象，是构成仿真对象的基本单元，其数据结构为一个类的对象，如一截巷道等。

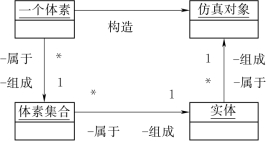
图3.2　实体造型关系图(www.xing528.com)

（4）仿真对象。它是一种特定类型仿真对象，是多个实体类的集合，如整个矿体、运输系统、开拓系统等。

基于上述组织结构，实体模型的构造过程具体表达为：一个仿真对象由一系列实体类组合表示，一个实体类又由一个或几个场量集合通过逻辑运算共同构成。从而，利用一体化模型构造一个复杂仿真对象，其关系如图3.2所示。

2.逻辑树表达

在一体化模型构造复杂实体对象过程中，需要建立一个用以描述实体对象间拓扑关系的结构，以解决一体化模型中复杂对象模型构建的问题。针对这一问题，本书采用二叉树结构来描述这种集合间、对象间、集合与对象间的关系，从而解决一体化模型中对象间、实体间、集合间和场量间的拓扑关系。

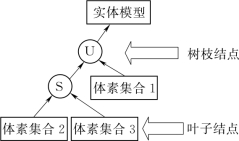
图3.3　逻辑树示意图

根据二叉树定义，树中的每个结点最多只有两棵子树，即树中任何结点的入度不大于2，且二叉树的子树有左右之分。在二叉树中，主要包括两种结点，即树枝结点和叶子结点，其中树枝结点是在该结点下仍有子二叉树存在的结点，主要用于描述场量集合及对象的逻辑运算（并集、交集、差集）；叶子结点是在该结点下无子树存在的结点，一般用于描述各场量集合及对象，由于这样的二叉树主要是对场量集合之间、对象之间及集合与对象之间逻辑关系的描述，故也可称为逻辑树，其结构如图3.3所示。

（1）逻辑运算类型。在逻辑树的树枝结点中，所描述的基于场量集合、实体类、对象等的逻辑运算主要包括交、并和差3类。

1）交集（Intersection，I），即两个或两个以上的场量集合（或对象）的共有部分生成一个新的场量集合（或对象）。

2）并集（Union，U），将两个或两个以上的场量集合（或对象）并成一个新的场量集合（或对象）。

3）差集（Subtraction，S），从第一个场量集合（或对象）中减去与第二个场量集合（或对象）共有的部分，生成新的场量集合（或对象）。

（2）逻辑树表达方式。逻辑树的表达采用左子树、逻辑符、右子树的方式进行，设有两个场量集合（或对象）A、B，则场量集合（或对象）A与场量集合（或对象）B的差集表达为A-S-B，并集表达为A-U-B，交集表达为A-I-B，其对应逻辑树的表达方式如图3.4所示。

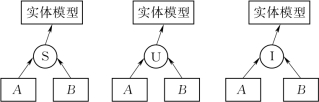
图3.4　逻辑差集、并集、交集表达树示意图

从逻辑运算的规则可见，逻辑运算不存在交换率，即左右子树次序不可调换。同时，若逻辑表达树一旦确定，则可通过场量集合（或对象）的运算将两个或多个场量集合（或对象）结合在一起共同形成一个组合体，且这个组合体的空间形体唯一确定。因此，该结构能够实现由简单的正则集经过正则集合的运算构造出复杂实体，即可通过基本的场量集合运算构造实体，进而构造各种仿真对象。