行波差动保护的工作原理

行波差动保护的基本原理可用图55所示的单相无损线路mn内部故障前、后的电流、电压的变化加以说明。由电工原理可知，线路上任意点的电压和电流可用下式表示

式中　——前行波；

——反行波；

ZC——波阻抗。

图55　单相无损线路示意图

由式（5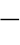22）和式（523）可得

设线路长度为D，可导出线路mn两端的电压和电流的关系式。

在线路m端，由图55可知，x＝0。将x＝0代入式（524）可以得到

式中　um，im——m端电压、电流。

在线路n端，x＝D，将x＝D代入式（524）可以得到

在式（527）左侧第二项前取负号是因为n端电流方向与所规定的电流正方向相反。

由式（5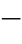26）中，以代替t可得

由式（527）和式（5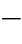28）可得出贝瑞隆方程，表示为

式中　——线路mn的行波时间。

式（529）可以这样解释：某观测者沿线路mn按x的正方向以波速υ前进，在时刻t-τ，在m端观测到的是式（5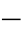29）左侧的值，经过时间τ后达到n端，在n端观测到的是式（5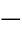29）右侧的值，二者相等。

式（529）即为行波差动保护原理的理论基础。根据式（529）可定义(www.xing528.com)

由式（530）可知，当线路内部无故障时iD1＝0。同理，由式（525），也可导出

并定义

由式（5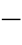32）可知，当线路mn内部无故障时

现在讨论线路内部有故障的情况。例如在图5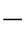5（b）中F点发生故障，F点的电压、电流以uF（t）、iF（t）表示，则

由图55（b），根据式（531）可写出

式中　τm——由故障点F到m端的波行时间；

τn——由F点到n端的波行时间。

由式（534）和式（535）消去uF，同时考虑式（533）可得

因为上式左端为iD2（t），故

同理，由图55（b），根据式（529）可导出

由以上分析可见，利用iD1（t）和iD2（t）可以正确区分线路内部、外部故障。当线路内部无故障时，i D1（t）＝iD2（t）＝0，保护不动作；在线路内部故障时，iD1（t）和iD2（t）为短路点的电流，保护动作。因此，iD1（t）和iD2（t）可以作为行波差动保护动作的基本判据。

当线路可以用集中电感等效，且不考虑分布电容的影响时，τ＝0，C＝0，ZC→∞，则有

显然，上式即为传统的电流差动保护的基本原理。

上述分析是在单相线路的基础上进行的。对于三相输电线路，应用模量变换方法，可以把三相线路分解为三个独立的单相线路，每一单相线路对应一个模量，因此上述分析的结果对每一模量都是适用的。