测距式距离继电器：基于动作判据的保护特性判断

前面介绍的各类距离继电器既不计算距离，也不计算测量阻抗，只是根据继电器的动作判据间接地判断测量阻抗是否处于保护特性的动作区内。微机保护具有很强的计算能力，可以算出测量阻抗或其电抗分量的数值，从而确定故障点的位置。根据故障点的位置不但可以确定保护是否应该动作，还能够明确指示出故障点离保护安装处的距离，同时满足故障测距的需求。

微机保护中的故障测距和按此原理构成的测距式距离继电器，如果仅使用本侧的电流和电压，则称为单端测距。单端测距算法由于不能获得故障支路的电流，因而测距精度受过渡电阻的影响较大。当线路保护采用差动纵联保护时，故障相的差动电流就是故障支路的相电流，本质上利用了对侧信息，因此可以采用双端测距算法。

用测距算法可以直接得到测量阻抗的电阻和电抗，由此可以计算出故障距离。在正方向故障时得到的距离为正，在反方向故障时得到的距离为负，有方向性。但当出口附近故障时，电压接近于零，由于计算难免有误差，测距结果可能失去方向性。因此，在计算出的距离小于整定值的1/8（特短线可以自动增大此比值）时增加方向判别的条件，方向元件的电压应有记忆作用。

1.基本原理

测距式距离继电器的基本原理是通过解微分方程来计算测量阻抗的。以应用于线路距离保护为例，它假设被保护线路的分布电容可以忽略，因而从故障点到保护安装处的线路阻抗，可以用一个电阻和电感串联电路来表示。于是，在短路时，下列微分方程成立，即

式中　R1、L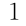1——故障点至保护安装处线路段的正序电阻和电感；

u、i——保护安装处的电压、电流。

若用于反映线路相间短路保护，则方程中电压、电流的组合与常规保护相同；若用于反映线路接地短路保护，则方程中的电压用相电压，电流用相电流加零序补偿电流。

式（4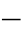88）中的u、i和di/dt都是可以测量、计算的，未知数为R1和L1。如果在两个不同的时刻t1和t2分别测量u、i和di/dt，就可以得到两个独立的方程，即

式中：D＝di/dt，下标“1”和“2”分别表示测量的时刻为t1和t2。

联立求解上述两个方程可求得两个未知数R1和L1，即

电流的导数可用差分来近似计算，最简单的方法是取t1和t2分别为两个相邻的采样瞬间的中间值。于是近似有

电流、电压取相邻采样的平均值，有

从上述的方程中可以看出，解微分方程算法实际上解的是一组二元一次代数方程，带微分符号的量D1和D2是可以计算得到的已知数。有的文献称这种方法为R—L串联模拟法。

解微分方程算法所依据的微分方程式（488）忽略了输电线路分布电容，由此带来的误差只要用一个低通滤波器预先滤除电压和电流中的高频分量就可以基本消除。分布电容的容抗只有对高频分量才是不可忽略的。解微分方程算法可以不必滤除非周期分量，因而算法的数据窗较短，而且它不受电网频率变化的影响。但当将这种算法和低通滤波器配合使用时，它将受信号中的噪声影响比较大。

2.测距算法

在单侧电源供电的线路上发生故障时，包括过渡电阻在内的线路模型是简单的R-L串联的电路，因而计算出测量阻抗中的电抗分量就可以精确地计算出距离。双侧电源线路上经过渡电阻短路时测量阻抗中增加了ZR分量，计算结果产生误差。为了使测距准确，所建物理模型中必须考虑到过渡电阻中电流与线路中电流不相同的情况。(www.xing528.com)

首先介绍按照电压相量图解算线路阻抗中电抗分量XL的方法。

图425为经过渡电阻短路时的电压相量图。

此时保护测量的电压和电流的关系为

图425　故障回路的电压相量图

其中

式中　——母线电压；

——线路电流；

——故障点电压。

一般情况下，与不同相。所谓测距问题实际上就是求解图4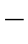25中电压三角形OMF的边MF＝（RL＋j X L）I。

故障点的远近和过渡电阻RF的大小都是随机的。三角形OMF的两个边OF和MF都是未知数，但是它们的方向可以由和确定。的相位在单相接地故障时由决定，在相间故障时由和ΔI决定，于是三角形不难求解。将代入式（491）得

令。其中，角标C和S分别表示实部和虚部。将这些量用复数表示后可将式（492）分解为实部和虚部两个方程。从两个方程中消去RF，并注意到

则可求得故障线段的电抗为

是无法测量的，但是对单相接地故障由

式中　ΔIS、ΔIC——IS、IC的故障分量。

求出后代入式（494）就可求出XL＝ωLL，从而达到测距的目的。