故障分量距离继电器的作用与应用

1.工作原理与动作方程

故障分量的距离继电器实际上就是用短路附加状态里的电气量构成的阻抗继电器。为了叙述方便，假设过渡电阻Rg＝0，并把此时的短路附加状态用图419表示。

阻抗继电器装在MN线路的M侧，加在继电器上的电压、电流分别为ΔU、ΔI，其表达式如下所述。以下公式中的电压、电流均为相量。

（1）接地阻抗继电器。

（2）相间阻抗继电器。

设工作电压ΔUOP的计算式如式（471）所示。它是短路附加状态中加于保护上的电压减去流过保护的电流与整定阻抗的乘积。对于接地故障或相间故障取式（471）中不同的公式。计算机可按此公式求出ΔUOP值。

式中：Zzd为阻抗继电器的整定阻抗。它表示从保护安装处到保护范围末端Y点的阻抗。（ΔIφ＋K3I0）Zzd和ΔIφφZ zd为短路时流过保护的电流ΔI在Zzd上的压降。

下面根据故障点在保护范围内，正向保护范围外和保护反方向的不同情况分三种情况加以讨论。

（1）故障点F在保护范围内。

此时短路附加状态如图419所示。因为电源中心点S点的电位是零，所以母线的电位为-ΔU，故障点F的电位为-ΔU F。按图中规定的母线电压ΔU的正方向是指电位升的继电保护习惯用法，有ΔU＝-ΔIZS。所以

图419　短路附加状态

故障点F在保护范围内，ZK＜Zzd。从式（472）可见，此时。系统中电位的分布图如图420（a）所示。

图420　故障分量电压分布图

（a）故障点在F 1；（b）故障点在F2；（c）故障点在F3；（d）故障点在F4

（2）故障点F在正向保护范围外。

由于ZK＞Zzd，所以根据式（472）可知。此时系统中的电位分布如图420（b）所示。

（3）故障点在保护反方向。

此时，短路附加状态如图423所示，这里暂不考虑过渡电阻。因为对侧电源中心点R点的电位是零，所以按图中规定的电压、电流正方向有式（473）的关系。

显然，此时。电位分布图如图420（c）所示。

从上述三种情况的分析可以得出结论，如果继电器的动作方程如式（474）所示，可保证继电器只在区内故障时动作。

在式（474）的动作方程中，ΔUOP值可按照式（471）计算。而ΔUF是故障点F在短路前的值。而短路前我们根本无法预测短路点的位置，因而ΔUF是不知道的。

为了构成可实现的动作方程，可用短路前保护范围末端（Y点）的电压代替ΔU F。计算机在发生短路时把短路前的电压值、电流值（负荷电压Ufh，负荷电流Ifh）保存起来，根据正常负荷运行的系统图计算出保护范围末端的电压，并把它记忆下来，该值记为。M表示记忆，并用该值代替ΔUF，即

该值计算出来的是短路前负荷运行情况下保护范围末端的电压，与式（471）对比，它们具有相似的结构。所以UOP也称作工作电压。为工作电压的记忆值。

现在，故障分量阻抗继电器真正用以实现的动作方程为

那么用代替原来的对继电器的动作性能会不会产生影响呢?保护范围会不会发生变化呢?

ΔUF是故障点F在短路前的电压，如果故障点F恰好发生在保护范围末端（Y点），那么在短路前故障点F的电压就正好是短路前保护范围末端Y点的电压，所以UOP就是ΔUF。因而这样代替的结果对保护范围的大小并不会产生影响，保护范围末端是正确的。对于保护范围内部的短路，根据系统的不同参数和保护的不同安装地点，有可能提高灵敏度），也可能降低灵敏度，但保护还是能动作的。同样的分析可知，对于外部短路保护不会动作。但是，不动作的可靠性可能高些，也可能低些。

正常运行时，系统中各点电压的幅值相差不会很大，只要保证保护范围末端位置不变。上述的灵敏度的高低和可靠性的高低相差不会很大，所以用UOP来代替ΔU F是允许的。

下面分析故障分量阻抗继电器的动作特性时还是用短路附加状态来分析，也就是用ΔUF来进行分析。

2.正向短路的动作特性分析和性能评述

在分析故障分量的阻抗继电器的动作特性时，接地阻抗继电器和相间阻抗继电器的分析方法和结论是一样的，所以下面以分析接地阻抗继电器为例。(www.xing528.com)

正向单相接地短路时的短路附加状态如图421所示。

图421　正向短路时短路附件状态

接地阻抗继电器的动作方程为

利用短路附加状态里的量来表述ΔUOPφ和ΔUFφ，如式（478）和式（479）所示。

式（479）中测量阻抗ZJ的值为

上式中Za为过渡电阻产生的附加阻抗，C为电流分配系数，即

将式（478）和式（479）代入动作方程式（477）并化简后可得

这是幅值比较动作方程。按幅值比较和相位比较动作方程的互换关系得到

所以式（481）的幅值比较动作方程可转换成式（4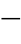82）的相位比较动作方程，即

由此可知，该动作方程对应的动作特性是以（Zzd）、（-2ZS-Zzd）矢量端点的连线为直径的圆，圆内动作区如图4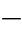22所示。

图422　正向短路时动作特性

从该动作特性看出，故障分量阻抗继电器在正向短路时的性能评述如下所述。

（1）与传统的以Zzd为直径的动作特性的阻抗继电器相比，故障分量阻抗继电器在＋R方向上有更大的保护范围，因此它保护过渡电阻的能力增强了。尤其是该动作特性向第三象限偏移很大，所以保护过渡电阻的能力得到很大增强。

（2）由于坐标原点位于动作特性内，所以正向出口短路无死区，因而不必像通常的方向阻抗继电器那样再采取其他复杂的措施。例如用短路前的电压（记忆）与短路后的电流先做方向判别等。

（3）由式（4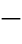80）决定的电流分配系数C的幅角仅决定于故障点F两侧各序阻抗的阻抗角的差别，而与两侧电势的相角差及过渡电阻Rg的大小无关，所以其幅角接近于零。C近似为一实数。由过渡电阻Rg产生的附加阻抗近似于纯阻性。对于图422所示的动作特性来说不会引起超越。

需要指出，图422所示的动作特性虽然在第三象限有很大的保护范围，但这不能说明该继电器没有方向性。因为整个动作特性是基于图421所示的正向短路时的短路附加状态中推导出来的，不能用它来分析反方向短路。最后，需要说明的是三相短路时的故障分量接地阻抗继电器，两相短路和三相短路时的故障分量相间阻抗继电器的动作特性都是图422的特性。

3.反向短路的动作特性分析和性能评述

同样，以接地阻抗继电器为例来分析，其结论也适用于相间阻抗继电器。

反向单相接地短路时短路附加状态如图423所示。加在保护上的电压、电流分别为ΔUφ、ΔIφ，按规定的正方向画出。过渡电阻Rg上的电流按ΔIφ方向画出。动作方程仍为式（477）。利用反向短路时短路附加状态里的量来表述和，如式（483）和式（484）所示。

图423　反向短路时短路附加状态

式（4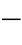84）中继电器的测量阻抗ZJ的值为

Za为由过渡电阻产生的附加阻抗。C为电流分配系数，即

将式（4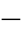83）和式（4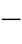84）代入动作方程式（4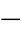77），并化简后得

把它转换成相位比较动作方程，即

图424　反向短路时动作特性

所以相位比较动作方程式为

该动作方程对应的动作特性为以（2ZR-Zzd）和（＋Zzd）两点连线为直径的圆，如图424所示。

从该动作特性中可以对故障分量阻抗继电器在反向短路时的动作性能做出评述。由于动作特性远离坐标原点向第一象限抛出，而反向短路时测量阻抗ZJ在第三象限，所以反向短路不会误动，它有良好的方向性。

也需要说明的是，反向三相短路时的故障分量接地阻抗继电器，反向两相短路和三相短路时的故障分量相间阻抗继电器的动作特性都是图424所示的动作特性。