距离继电器的单相式设计及接线方法

1.一般表达式

单相阻抗继电器比较复合电压E1和E2的相位或幅值。它们是

式中：K1、K2、K3、K4都是常数，一般为复数。K1和K3无量纲，K2和K4是阻抗。

由式（421）可见，E1和E2都是U和I的线性函数。由于继电器的动作只取决于和，我们称继电器反应于单一的电压和电流。和都是复数，为了方便，在分析时都将和两个变量用一个变量代替，Z称为继电器的测量阻抗。为了与反应多个电压或电流的距离继电器相区别，我们称之为单相阻抗继电器。单相阻抗继电器的动作特性是复数Z的函数，其理想动作特性可在阻抗复平面上表示出来。需要指出，U和I可能分别由两个电压或电流组成，但重要的是继电器的动作是一个变量Z的函数。

2.常用的单相阻抗继电器

（1）相间姆欧继电器。

在式（421）中，令K1＝1，K2＝-Zzd，K3＝-1，K1＝0，得

式中　Uop——工作电压；

——极化电压；

φφ——AB，BC，CA；

Zzd——整定电压。

其动作判据为

将式（422）代入式（423）得

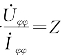分子、分母同除以，令，得

在图41阻抗平面上的动作特性为

图4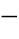1　姆欧继电器的动作特性

（a）θ1＝90°，θ2＝-90°；（b）θ1＜90°，θ2＞-90°；（c）θ1＞90°，θ2＜-90°

（2）接地姆欧继电器。

式中：φ＝A，B，C。

正向短路中，。

同样可得到式（424）和图41所示的动作特性。

（3）电抗继电器。(https://www.xing528.com)

式中　Zd——模拟阻抗，与Zzd同相，即电抗变压器转移阻抗。

式（4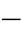26）中，对相间：，φφ＝AB，BC，CA。

对接地：，φ＝A，B，C，。

电抗继电器在阻抗平面上的动作特性如图4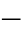2所示。

图42　电抗继电器的动作特性

常用的单项阻抗继电器的动作判据如表41所示。

表4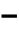1　常用的单相阻抗继电器的动作判据

3.单相阻抗继电器的接线方式

为了使阻抗继电器的测量阻抗正比于短路时母线到短路点间的线路阻抗，必须正确地确定引入阻抗继电器的电流和电压。单相阻抗继电器的原理建立在欧姆定律的基础上，因此通入继电器的电压应是短路环路的残余电压，而电流则应是短路环路的电流。输电线是三相系统，正确的接线法应能在同一点不同类型的直接短路（短路处过渡电阻为零）下，继电器的测量阻抗都相等。

（1）接地阻抗继电器。

图43是计算用系统图，显然故障相的母线残压为

图4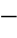3　计算用系统图

式（429）可简化为

式中　K——零序补偿系数，为复数，K＝（Z0L-Z1L）/3Z1L。为了便于在继电器中实现，通常取为常数。

令通入继电器的电压为Uφ，电流为经过零序电流补偿的复合电流，则继电器的测量电阻为

式（431）对单相短路接地、两相短路接地和三相短路都成立。注意，在推导过程中，对于健全相电流没有作任何限制，所以在任何负荷、系统振荡和两相运行状态下发生直接短路接地时对于故障相式（431）都是成立的。重要的是从母线到短路点之间流过的电流应相同，或者说母线和短路点之间没有分支。

（2）相间短路故障。

假设故障点F的相电压为，由式（430）可写出

若BC两相故障，在故障点由，于是

令通入继电器的电压为故障相间电压，电流为两故障相电流之差，则继电器的测量阻抗为

式（434）对两相短路接地故障和不接地故障，以及三相短路故障都成立。式（4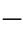34）不反映零序分量，因而在两相短路经过渡电阻接地时不受接地电阻的影响，在任何负荷、系统振荡和两相运行状态下发生直接短路时对于故障相式（4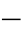34）都是成立的。