最小二乘算法及其在微机保护中的运用

最小二乘算法是参数估计理论中的一种经典方法，它广泛应用于数据处理和自动控制等领域。该算法是将包含有随机噪声分量的输入信号与预设的信号模型（拟合函数）按最小二乘原理进行拟合，根据拟合误差最小的原则来确定预设模型中的有关参数。在微机保护中，根据应用目的的不同，预设模型有不同的选择方法，相应的，最小二乘算法也有不同的表现形式。

在线路保护中，输入的故障信号中，除了有效信号基频分量和具有确定性数学模型的非周期分量外，其他分量如各种高频信号都具有明显的随机信号特性，因为它的频率、幅值、相位以及衰减速率与故障类型、故障点位置、故障初始时刻和故障前系统的运行状态等随机因素有关。因此，有关基频分量的参数计算问题，严格地说，应该是具有随机噪声信号模型参数估计问题。以随机信号模型为基础的参数优化估计算法，如最小二乘算法和卡尔曼滤波算法等也被引入到微机保护中，以提高参数计算的准确性。

在线路保护中，采用最小二乘算法对基频分量参数进行计算时，输入信号的预设模型可选择为

式中　X0、Td——非周期分量的初值和衰减时间常数；

Xm、φ——基频分量的幅值和相位。

将式（3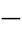51）用实、虚部表示有

式中　XR、XI——基频分量的实部和虚部。

而实际信号y（t），可视为有预设信号x（t）与附加的随机噪声信号r（t）共同组成，即

或

式（3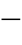53）中的随机信号r（t）包括了故障信号中除基频分量和非周期分量之外的其他所有成分。

对于由式（3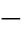53）所表示的输入信号而言，待确定的模型参数为非周期分量的初值X0和衰减时间常数Td以及基频分量的实部XR和虚部XI。在实际应用中，为了简化计算，参数Td通常可作为一个事先给定的常数处理，例如在它可能变化范围内选择一个恰当的数值。显然，若实际衰减时间常数偏离给定的数值，这种处理方式对基频参数XR和XI的计算会带来一定误差。但仿真计算表明，这种误差可控制在允许的范围之内。这样，待确定的参数可简化成只包括X0、XR和XI。

将式（353）用离散采样值形式表示时，有

现假设已经知道了k个输入信号的采样值y（i），i＝1，2…k。根据最小二乘估计理论的基本原则，以这k个采样值确定的有关参数X0、XR和XI的最优估计值和应使得残差平方和达到最小，即(www.xing528.com)

其中

可以证明，满足式（354）的最小二乘估计值为

其中

对于最小二乘算法来说，参数的估计精度与算法所采用的采样数目有关，所使用的采样值越多（k值越大），估计精度也越高。在微机保护中，采样数据是按采样频率逐个提供给计算机的。在得到新的采样数据后，若希望利用新的采样数据来改进原来的参数估计结果，以提高估计精度，一般不直接使用估计方程式（355）进行计算。因为，每增加一个新的采样数据，该方程式必须重新计算一次，而且用到较多的矩阵相乘运算，计算量太大。一般的处理方法是，新增加采样数据后，仅对原来的估计值进行某些修正，构成递推型的最小二乘算法。

假设新增加的采样数据为y（k＋1），改进后的参数估计向量为。由式（355）有

其中

令

可得到具有递推计算形式的最小二乘估计方程为

其中

从式（3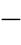57）中可以看出，新的估计向量可以由原有的估计向量加上一个修正项来得到。修正项正比于，而该项实际上反应的是以原有的估计向量对当前采样时刻的采样值进行预测时所产生的预测误差（拟合误差）。向量K（k＋1）则决定了在进行修正计算时，对预测误差的重视程度。在递推计算方程式（357）中，矩阵K（k＋1）与采样值无关，可以离线求出，所以，递推最小二乘算法的实时计算量最小，易于在微机保护中采用。

递推最小二乘算法的突出优点是具有可变的数据窗，它的数据窗长度将随着采样值的增多而自动延长，参数的估计精度也随之逐步提高。并且，算法计算简便、收敛速度快、收敛过程稳定。因此，可较好满足不同场合对参数计算精度和计算速度的不同要求。此外，该算法对非周期分量和各种高频分量具有良好的滤波能力，在实际使用中，无需再附加其他的数字滤波器。

最小二乘算法除了用于基频分量参数的计算之外，也可以用来计算其他谐波分量的参数，如在变压器保护中，2次谐波分量或发电机定子接地保护中的3次谐波分量等。