电路原理图设计与分析

图3.4　任务一方框图

1.电路原理图

555时基IC也称555定时器，它是一种多用途的数字－模拟混合集成电路，利用它能极方便地构成施密特触发器、单稳态触发器和多谐振荡器。由于使用灵活、方便，所以555定时器在波形的产生与变换、测量与控制、家用电器、电子玩具等许多领域中都得到了应用。

根据555的电气特性，连接成多谐振荡器，选择元件参数，电路原理图如图3.5所示。

图3.5　子任务一之电路原理图

NE555定时器三种工作模式

NE555定时器工作原理

2.原理分析

核心器件555的功能表如表3.6所示。

表3.6　NE555的功能表

555作为多谐振荡器其原理简介

起始状态下，电容C1没有充电，其两端压差为0，由于6脚和2脚都连接到C1的一端，也即此时2脚、6脚电压为低电平（低于VCC／3），根据555的功能表可知属于“状态4”，VO输出高电平。

随着C1的充电继续，其两端压差越来越大，当压差超过VCC／3，但没有达到，属于“状态3”阶段（VO输出维持不变，此时仍然为高电平）。

充电继续，端压差一旦大于，555的状态转换成“状态2”，VO输出变成低电平；同时内部三极管导通（其三极管的集电极连接到“7脚”），使电容C1开始经R2放电，两端压差开始下降。

放电继续，端压差继续下降，在低于VCC／3之前都属于“状态3”，其VO输出维持不变，即此时仍然为上一个状态的低电平；内部三极管继续导通，使放电继续。

随着放电的继续，其两端压差一旦低于VCC／3，555的状态即由“状态3”转换成“状态4”，VO输出由低变为高；同时内部的三极管截止，放电过程结束。由于R2、VD1、R1连接到更高的电位（本电路连接到电源VCC），C1又开始充电，其两端压差将要升高。

充电继续，只要端压差不超过，555就属于“状态3”；输出维持高电平不变。

以上状态，循环往复，其输出也不停地重复“高、低、高、低、……”。

请读者注意，“状态2”和“状态4”都是瞬间状态，出现的时间极短，而两个“状态3”维持的时间则相对很长，即充电时间和放电时间。

C1的充电路径，如果没有VD1，则充电路径为：＋12 V电源经过R1、R2给C1充电。有VD1时的充电路径则为：＋12 V电源经过R1、VD1给C1充电，如图3.6所示。

C1的放电回路如图3.7所示，C1充电、放电波形以及3脚的输出波形如图3.8所示。

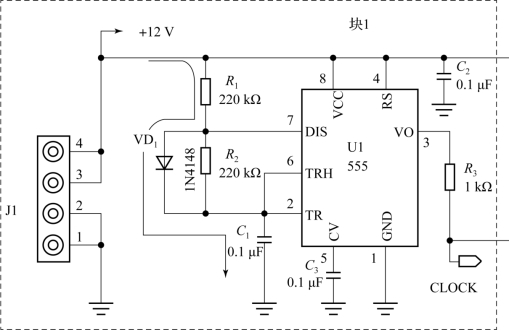
图3.6　电容C1的充电回路

图3.7　电容C1的放电回路

图3.8　电容C1的充、放电波形及对应的Vo输出波形

1）充电时间的理论计算

当VD1开路时，充电时间为

式中，VCC为电容充电无穷远时刻的电压值；U（T－）为电容充电开始瞬间的电压值，在555振荡电路中此值为VCC／3；U（T＋）为电容充电要达到的目标电压值，在555振荡电路中此值为2 VCC／3。

所以式（3.1）为(www.xing528.com)

当VD1连接时，R2被二极管VD1短路，忽略二极管的正向压降，此时的VD1可以认为是0Ω。

所以充电时间为

2）放电时间的理论计算

电容C1放电的回路：不论是否接入二极管VD1，其放电回路都是一样的，即为C1正极→R2→555内部晶体管C极→555内部晶体管E极→C1负极。

所以放电时间为

在式（3.4）中，0为电容放电无穷远时刻的电压值，即假想电容的电全部放完；

U（T＋）为电容放电开始瞬间的电压值，在555振荡电路中此值为2 VCC／3；

U（T－）为电容放电要达到的目标电压值，在555振荡电路中此值为VCC／3。

所以式（3.4）为

3）振荡周期（频率）及占空比的理论计算

当VD1开路时，由式（3.2）和式（3.5）可求得电路的振荡周期为

所以电路的振荡频率为

所以输出脉冲信号的占空比为

式（3.8）说明，VD1开路时，图3.7电回路所示的电路输出脉冲的占空比始终大于50%。

当VD1连接时，由式（3.3）和式（3.5）可求得电路的振荡周期为

所以电路的振荡频率为

所以输出脉冲的占空比为

式（3.11）说明，VD1连接后，图3.7所示的电路输出脉冲的占空比可小于50%。

如图3.7所示电路中的参数值，由式（3.9）、式（3.10）和式（3.11）可分别算出该电路的周期、频率及占空比为

读者在以后的电路性能测试时可以验证上述的理论计算。

但要注意的是，实际的元件参数与元件所标称的值也存在一定的误差。比如：一般来说普通碳膜电阻的标称阻值与实际阻值的误差在±5%以内，而普通的瓷片电容其标称容量与实际容量的误差在±20%以内，普通的电解电容容量误差甚至达到＋80%、－20%。这些误差最终都会累积到一起（极端情况下，所有的元件都是正误差，或者所有的元件都是负误差；大多数的情况下，一部分元件是正误差，而另一部分元件则是负误差，可以相互抵消一部分误差），从而最终引起实测的结果与理论计算的差距。

在特定场合下，要求输出信号或性能必须达到特定的范围要求，为了能满足批量生产就必须选用高精度的电子元器件，如电阻可以选择精密电阻（误差能小到±1%或±1‰以内），电容也可以选择温度特性稳定、容量误差更小的电容。但这些高精度的电阻、电容等电子元器件，其成本价格也是普通材料的数倍或10倍以上。

实际产品设计时，在不影响产品性能的情况下尽量选用通用电子元器件，这样做的目的如下。

（1）通用电子元器件容易采购、备料，方便及时生产。

（2）通用电子元器件价格便宜，有利于降低产品的材料成本。

本书的设计任务是“电动车尾灯闪烁器”，对时钟信号的频率误差要求不严格，可以允许频率误差达到±30%左右，所以选用最普通的电阻、电容。