折管式运动粘度测定仪的结构及计算公式

如图3-2所示，折管式粘度管由进样口、弯头、横臂、毛细管、检测泡几部分组成。用微量移液器吸取一定量的样品（如0.45μL）注入进样口，样品经弯头流入小坡度的横臂，然后进入毛细管。由于毛细管内径小、流速慢，样品与毛细管接触充分，样品很快达到恒温要求。样品到达上检测器时，开始计时，到达下检测器时终止计时，流动时间t为样品充满测量球泡的时间。

图3-2 自动折管式运动粘度测定仪

测量结果依照运动粘度计算式（3-1）用粘度管常数乘以流动时间t得到。

ν=Ct （3-1）

式中：ν为运动粘度（mm²/s）；C为粘度管常数（mm²/s²）；t为实验中测得的流动时间^[2]。

根据泊式公式（又称哈要-泊肃叶，Hagen-Poiseuillen定律），则

得到运动粘度计算公式：

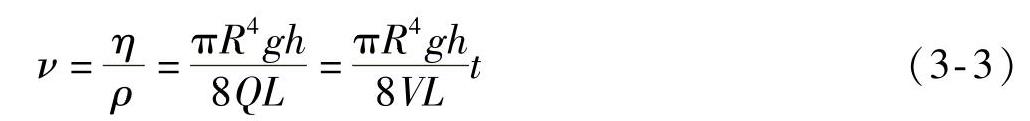(www.xing528.com)

式中：η为动力粘度；ν为运动粘度；R为毛细管半径；L为毛细管长度；p为毛细管两端的压力差；V为在t时间内流经毛细管的流体体积；g为重力加速度；t为V体积流体的流动时间；Q为毛细管的流量；h为液柱高度；ρ为流体密度。

根据式（3-1）及式（3-3），得

根据式（3-4）可知：粘度管常数处（取）决于毛细管的内径、长度、重力加速度，液柱高度及流体。体积对于同一根毛细管，半径、长度，流体体积及重力加速度（同一地点）都已经确定，只要液柱高度不变（图3-3EF段），那么毛细管的常数是确定的。

折管式粘度管的结构设计如图3-3所示。为了保证样品进入横臂后能自由流动，顺畅进入毛细管和清洗时清洗液不滞留在横臂处，常常将横臂设计成有一定的坡度。图中可见h₃＞h₂＞h₁，对应的C3＞C2＞C1；在计算或者校准粘度管常数时，一般将样品末端控制在横臂中间，对应的常数为C取C2值。由于只有一个常数，因此当环境或者操作人员改变时会带来相应的测量误差，如样品温度高时，粘度小，加样后移液器吸嘴残留量少，进入粘度管的样品多，则液柱高度高，为h₃，常数应为C3；计算时使用的C取值是C2，结果会偏小。反之，当样品温度低，或者样品粘度大时，滞留在微量移液器中的样品多，进入粘度管的样品量少，因此液柱短，测量结果会偏大。导致这类误差的主要原因包括：样品温度、操作人员取样、加样速度及挤压微量移液器的力度、样品粘度、粘度管横臂坡度。

以横臂中点计算液柱高度为100mm左右，粘度管设计制造上保证横臂的最左端和最右端高度差在2mm以内，加样时保证样品末端处于横臂内，数据的重复性和准确性在理论上是可以保证在1%的要求内的。

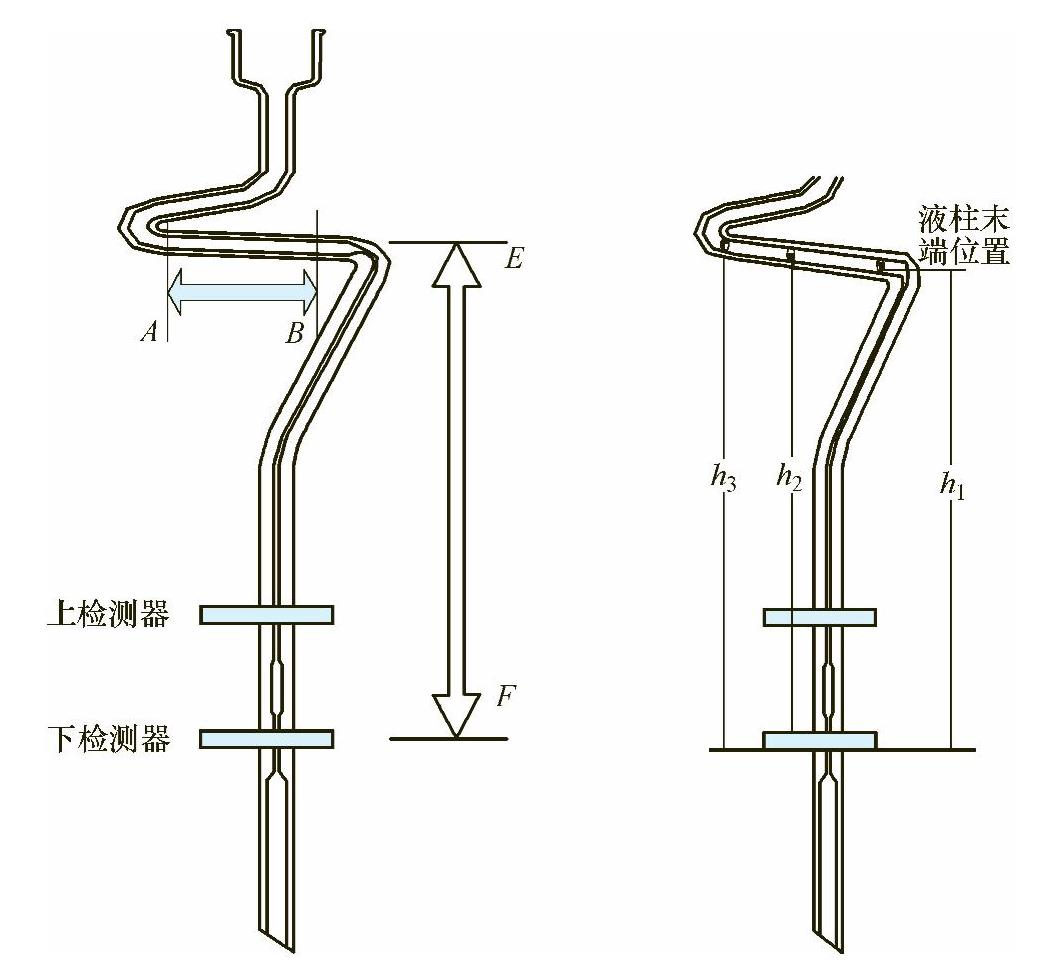
图3-3 折管式粘度管测量原理示意图