如何根据额定动载荷选择合适的轴承尺寸？

按GB/T 6391—2010的标准规定，滚动轴承的基本额定动载荷C_r，是以寿命计算式为依据转换得来的。

2.3.1 滚动轴承的寿命计算及基本额定动载荷

（1）寿命计算公式 根据GB/T 6391—2010，滚动轴承的基本额定寿命L₁₀可由下式计算

式中 L₁₀——基本额定寿命（10⁶转）；

C_r——基本额定动载荷（N）；

P——当量动载荷（N）；

ε——寿命指数（球轴承ε＝3，滚子轴承ε＝10/3）。

若轴承的转速恒定，其基本额定寿命可用运转小时数表示为

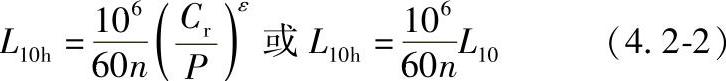
式中 L_10h——基本额定寿命（h）；

n——轴承转速（r/min）。

对于车辆轮毂用轴承，基本额定寿命可用其行驶千米数表示：

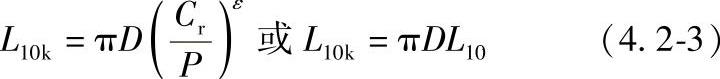
式中 L_10k——基本额定寿命（km）；

D——车轮直径（mm）。

若轴承作摆动运动，绕摆动中心摆动幅角为±γ，则

式中 L_10osc——基本额定寿命（10⁶次摆动周期）；

γ——摆幅（°）。当摆幅很小时，不计算基本额定寿命。

为了简化计算，取500h作为额定寿命的基准，引入速度系数f_n和寿命系数f_h：

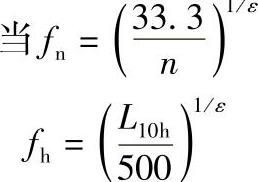
则轴承寿命公式可转换为

基本额定动载荷

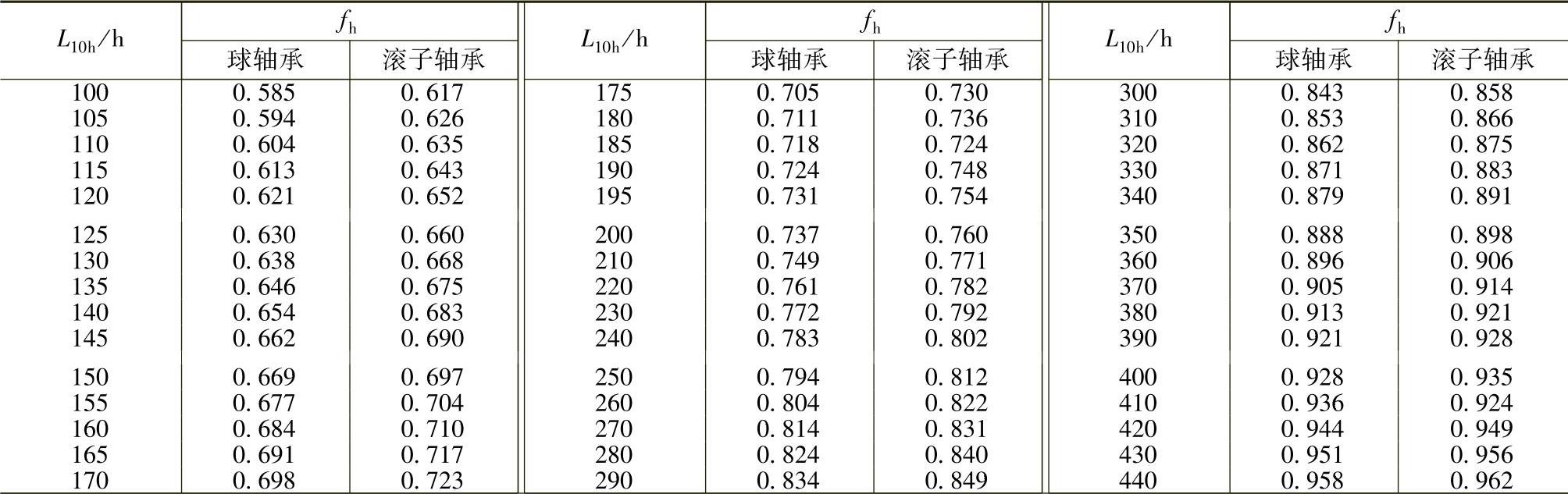
根据轴承的工作转速n和预期的使用寿命L_10h，由表4.2-6和表4.2-7查出f_h、f_n的数值后，即可很方便地确定出待选用轴承所应具有的基本额定动载荷值。

表4.2-6 寿命系数

（续）

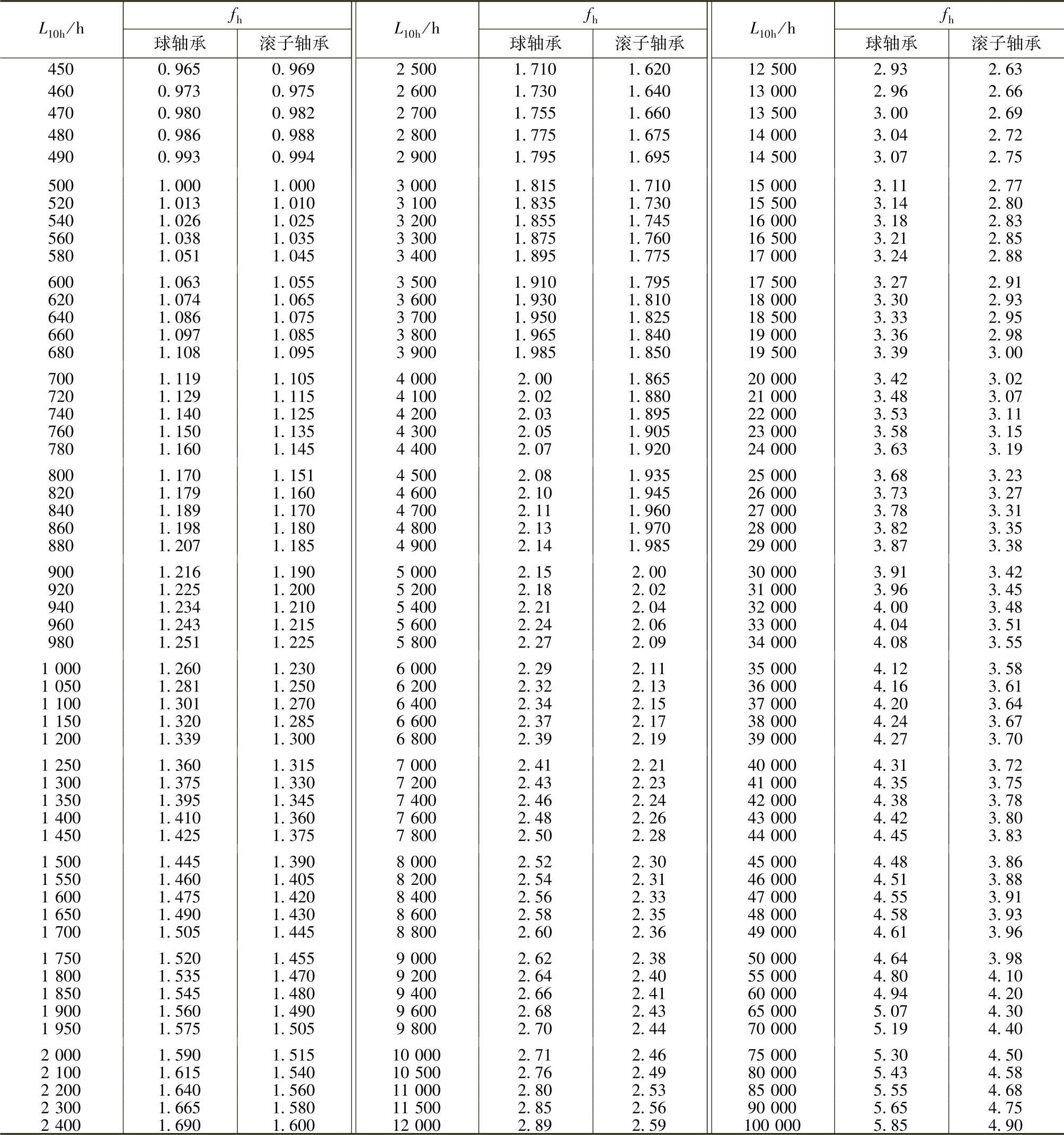
表4.2-7 速度系数

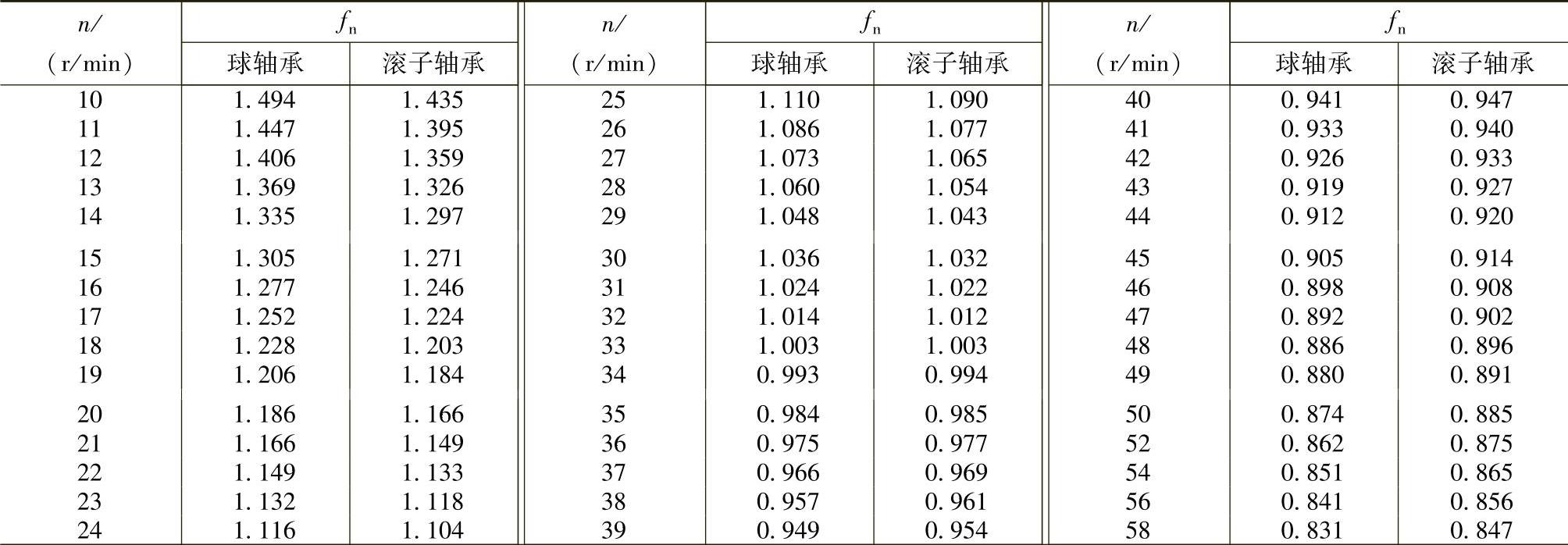
（续）

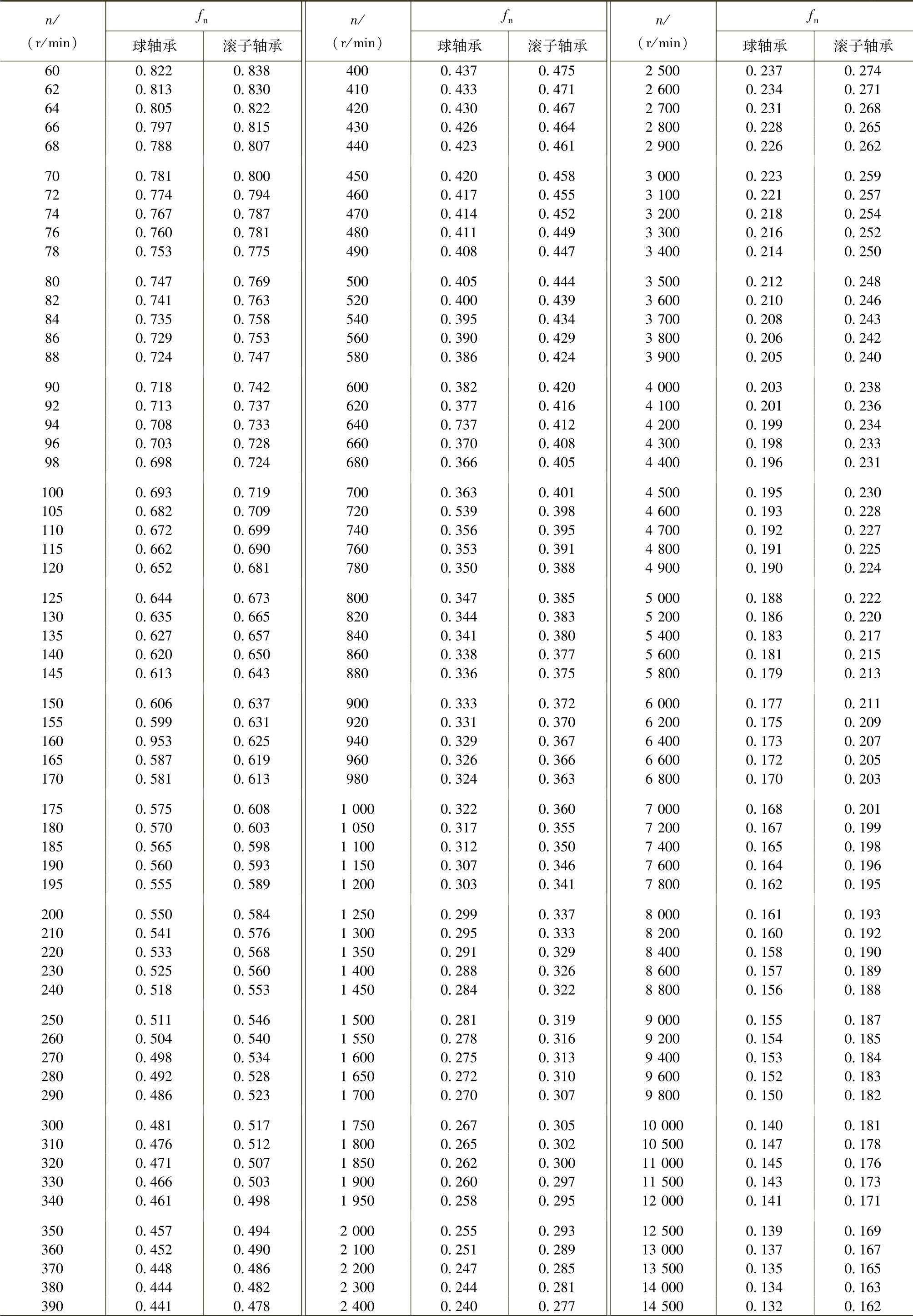
（续）

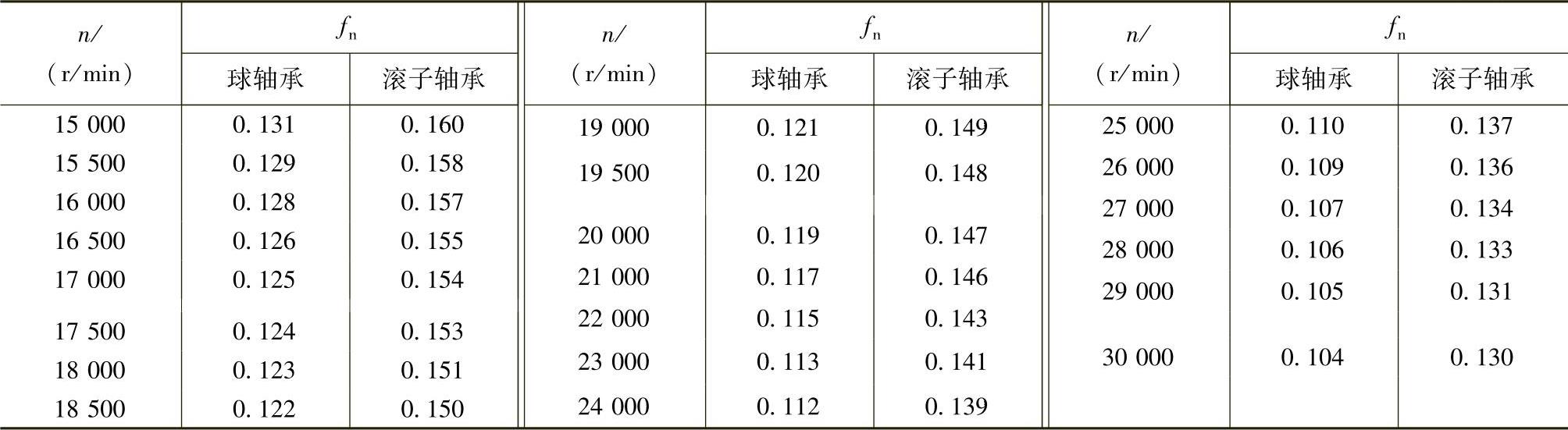
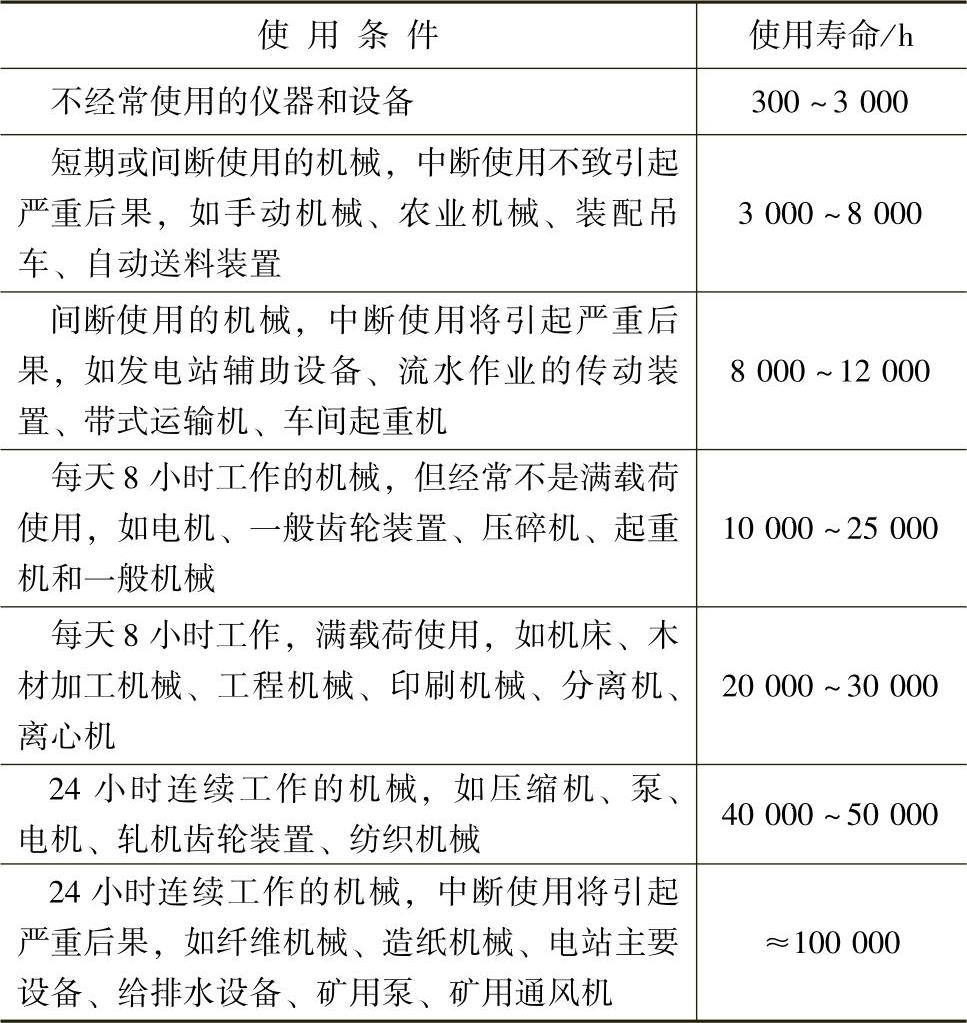
（2）轴承的使用寿命 在选择轴承时，一般应根据机械的类型，工作条件及可靠性要求，预先确定一个恰当的使用寿命。通常，可参照机械的大修期限予以决定。各种机械所需的轴承使用寿命的推荐值见表4.2-8。

表4.2-8 轴承使用寿命的推荐值

（3）当量动载荷的计算 在式（4.2-5）中，必须求出当量动载荷P，否则无法计算出基本额定动载荷C。

1）当量动载荷P的一般计算式。在恒定的径向载荷F_r和中心轴向载荷F_a作用下，当量动载荷为：

①向心球轴承和滚子轴承，当接触角α≠0°时，其径向当量动载荷为

P_r＝XF_r＋YF_a （4.2-6）

当α＝0°时，只承受纯径向载荷，其径向当量动载荷为

P_r＝F_r（4.2-7）

两套相同的单列角接触球轴承或滚子轴承安装在同一轴上，“背对背”或“面对面”配置作为一个整体（成对安装）运转，这对轴承的径向当量动载荷按一套双列角接触球轴承计算。

两套或两套以上相同的单列向心球或角接触球轴承并列安装在同一轴上，以“串联”配置作为一个整体（成对或组合安装）运转，计算径向当量动载荷时，用单列轴承的X和Y系数值。对于球轴承，“相对轴向载荷”用i＝1和其中一套轴承的F_a和C_0r确定（虽然总载荷F_r和F_a是用来计算整个配置的当量载荷的）。

②推力球和滚子轴承，当α≠90°时，其轴向当量动载荷为

P_a＝XF_r＋YF_a （4.2-8）

当α＝90°时，只承受纯轴向载荷，其轴向当量动载荷为

P_a＝F_a（4.2-9）

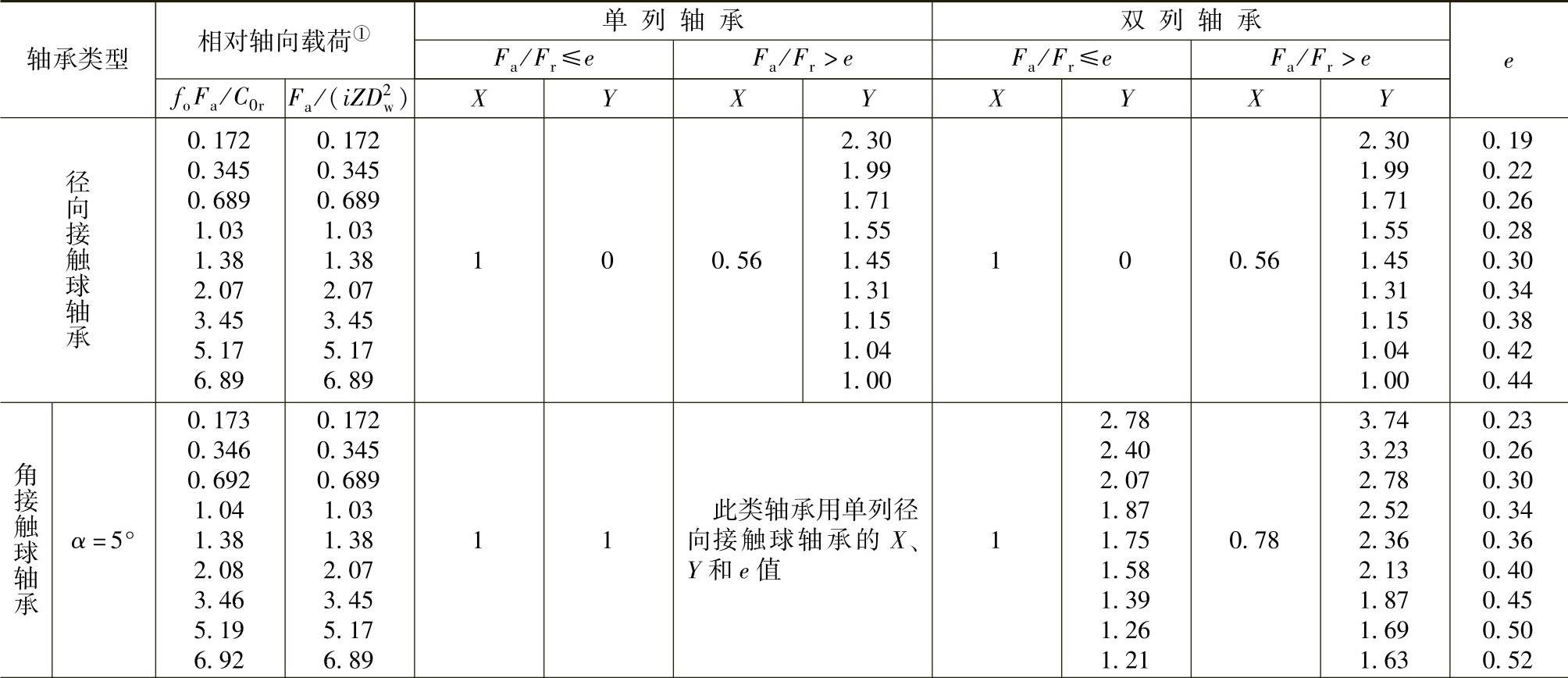
系数X和Y的值列于表4.2-9和表4.2-10。

表4.2-9 向心轴承的X和Y值

（续）

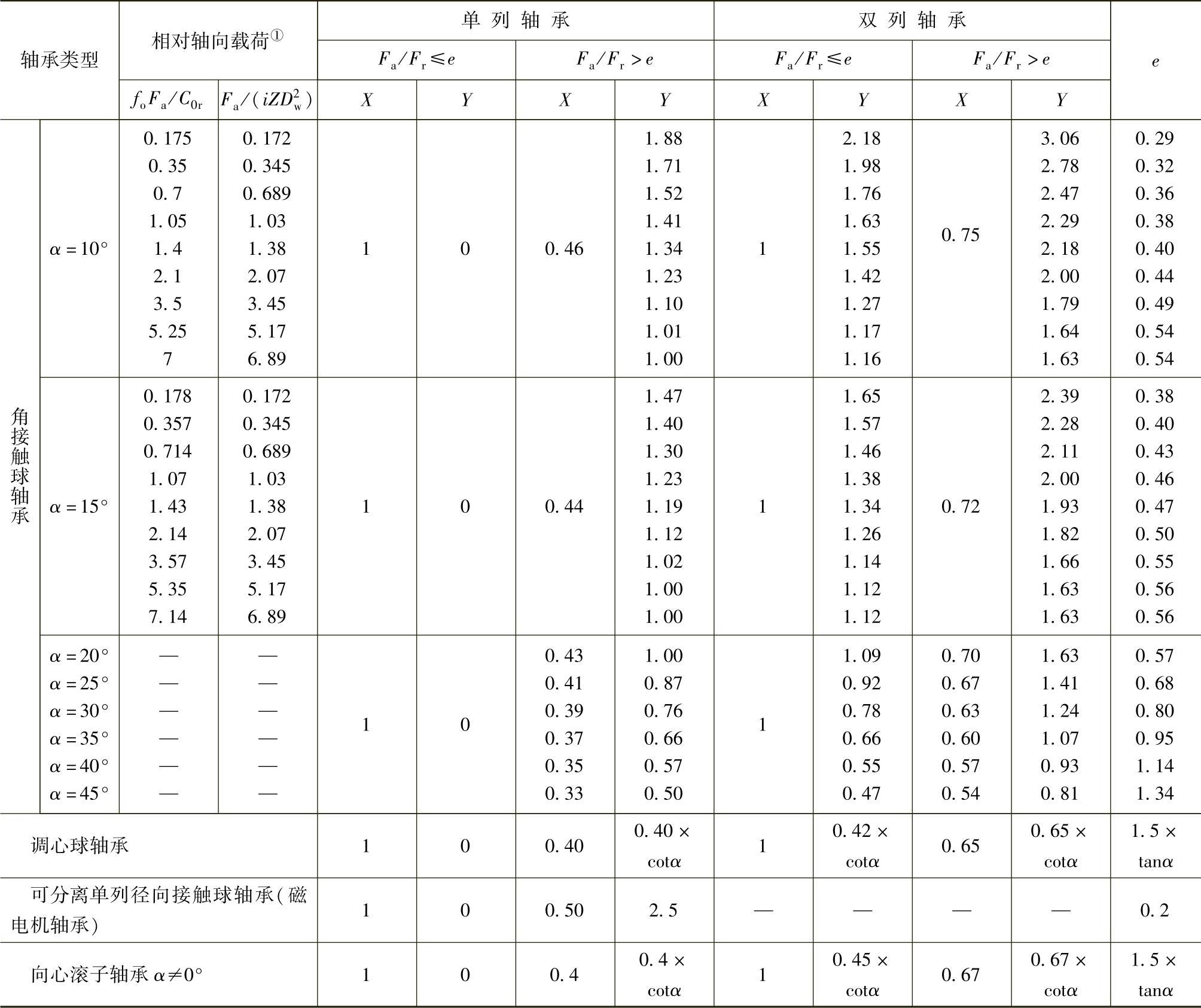
①对于径向接触球轴承，“相对轴向载荷”允许的最大值决定于轴承设计（游隙和沟道深度）。对角接触球轴承，“相对轴向载荷”和接触角的中间值，其X、Y和е值可由线性内插法求得。

表4.2-10 推力轴承的X、Y系数

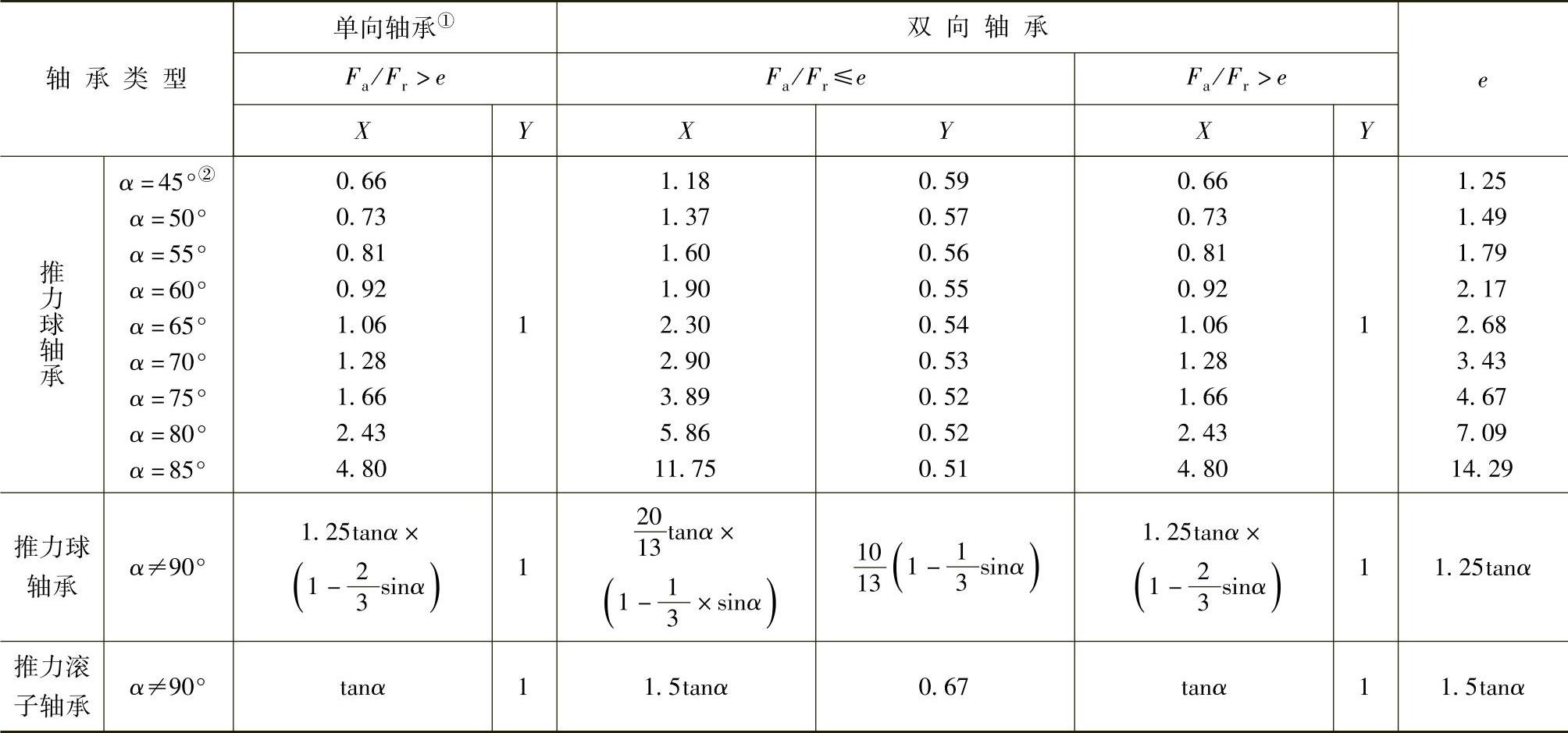
①对于单向轴承，F_a/F_r≤e不适用。

②对于推力球轴承，α＞45°，α＝45°的值供α在45°～50°之间时的内插计算使用。

2）考虑力矩载荷的当量动载荷。当轴承承受恒定力矩载荷时，当量动载荷可按下式计算：

P_M＝f_MP （4.2-10）式中 P_M——考虑力矩载荷的当量动载荷（N）；

f_M——力矩载荷因数，见表4.2-11。(www.xing528.com)

表4.2-11 力矩载荷因数

3）考虑冲击载荷的当量动载荷。当轴承承受冲击载荷时，当量动载荷可按下式计算：

P_d＝f_dP （4.2-11）

式中 P_d——考虑冲击载荷的当量动载荷（N）；

f_d——冲击载荷因数，见表4.2-12。

表4.2-12 冲击载荷因数

4）变载荷情况下的平均当量动载荷P_m。当轴承的载荷和（或）转速随时间周期性变化时，应将其当量动载荷取某平均值，计算公式为

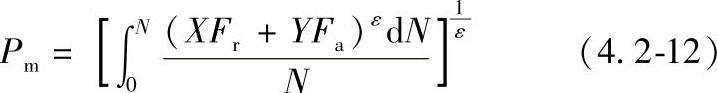
式中 N——一个周期的转数；

ε——寿命指数，球轴承ε＝3，滚子轴承ε＝10/3。

对下列几种常见动载荷，可用相应的简化公式：

1）轴承依次在当量动载荷P₁，P₂，P₃……作用下运转，其相应转速为n₁，n₂，n₃……在每种工况下运转的时间为t₁，t₂，t₃……如图4.2-5a所示，则有

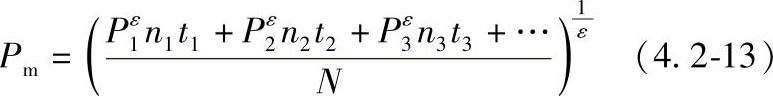
式中，N＝n₁t₁＋n₂t₂＋n₃t₃＋…

2）轴承转速不变，当量动载荷在P_min和P_max之间线性变化，如图4.2-5b所示，则有

P_m＝1/3×（P_min＋2P_max） （4.2-14）

3）轴承载荷由大小、方向都不变化的固定载荷F₁（如转子质量）和大小不变的旋转载荷F₂（如不平衡量引起的离心力）组成（如图4.2-5c所示），则有

P_m＝ϕ_m（F₁＋F₂） （4.2-15）

式中，ϕ_m根据比值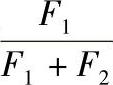由图4.2-6查出。2.3.2 向心角接触轴承的载荷计算

（1）载荷作用中心 角接触轴承在计算支承反力时，首先要确定载荷作用中心O点的位置（见图4.2-7），其位置参数a的数值可见本章第9节“滚动轴承的尺寸规格及性能参数”表。

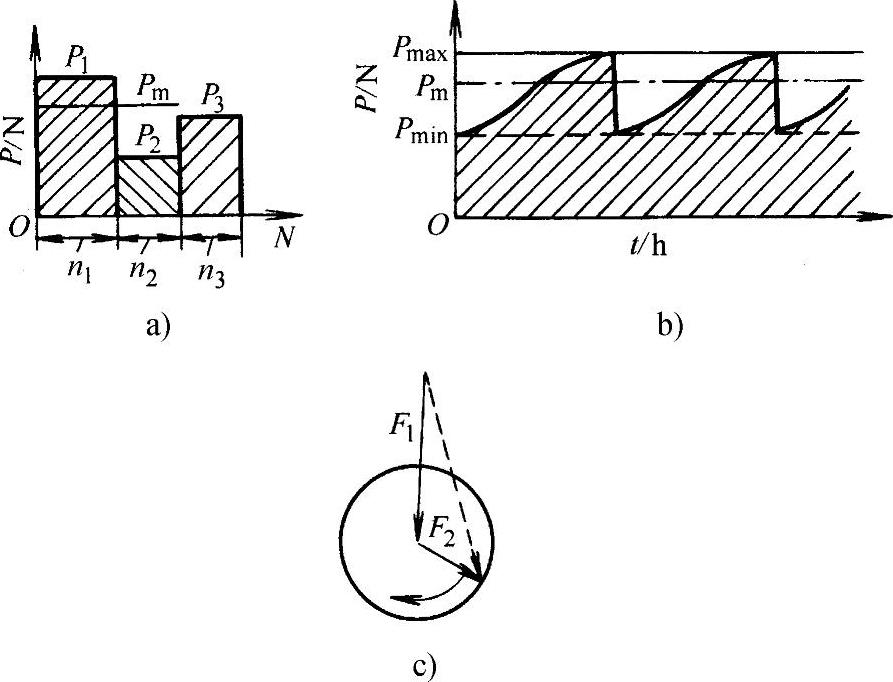
图4.2-5 各种动载荷随时间的变化规律

a）轴承依次在P₁，P₂，P₃…作用下运转 b）当量动载荷在P_min和P_max之间线性变化 c）轴承受固定载荷和旋转载荷同时作用

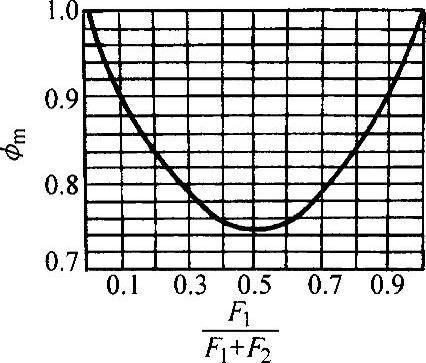
图4.2-6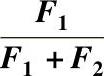与ϕ_m的关系

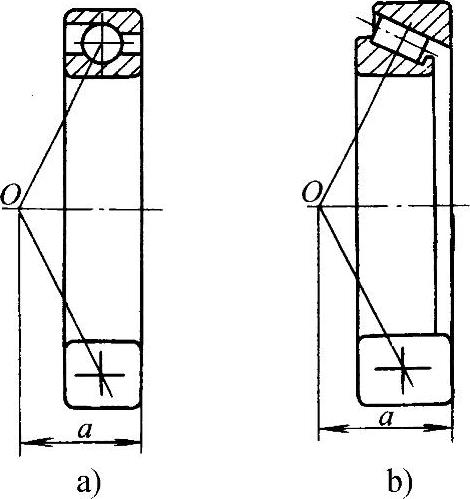
图4.2-7 角接触球轴承和圆锥滚子轴承的载荷作用中心

a）角接触球轴承 b）圆锥滚子轴承

（2）附加轴向力 角接触轴承在承受纯径向载荷时，将产生附加轴向载荷S，计算公式为

角接触球轴承

S＝eF_r （4.2-16）

式中，e的数值可由表4.2-9查出。

圆锥滚子轴承

S＝F_r/2Y （4.2-17）

式中，Y应取表4.2-9中F_a/F_r＞e的数值。

（3）成对安装的角接触轴承轴向载荷 成对安装的角接触轴承，在计算轴向载荷时要同时考虑由径向载荷引起的附加轴向载荷S和作用于轴上的工作载荷F_A。在不同的安装情况下，轴承1、2的轴向载荷F_a1和F_a2的计算公式见表4.2-13。

表4.2-13 成对安装的角接触轴承轴向载荷计算公式

2.3.3 静不定支承结构的载荷计算

图4.2-8所示为一端成对安装两个同一型号的角接触轴承，另一端安装一个只能承受径向载荷的向心轴承，若轴的变形忽略不计，可参照图4.2-9采用试算迭代的方法求出每个轴承承受的载荷，计算步骤如下：

图4.2-8 静不定支承结构

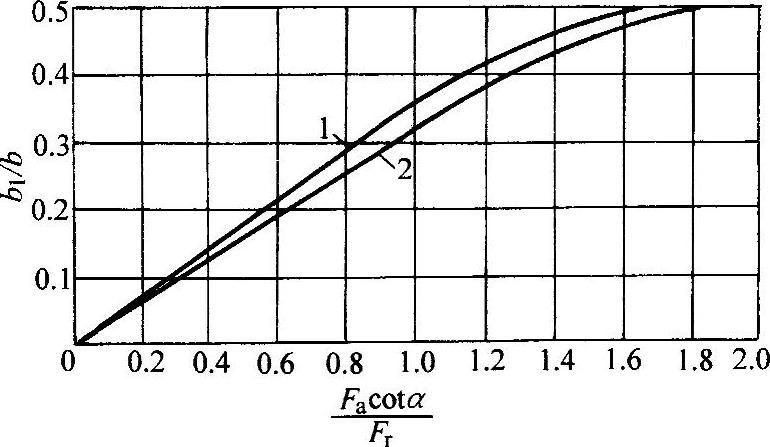
图4.2-9与之对应值

1—角接触球轴承 2—圆锥滚子轴承

1）假定合成径向载荷F_r作用在中心点O处，可算出

2）由

值查图4.2-9找出相应的值。其中，对角接触球轴承

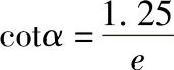
对圆锥滚子轴承

cotα＝2.5Y

式中，e、Y值可由表4.2-9查出。

3）根据b₁值，可由下式计算F_r（2）

这样，经过几次迭代，F_r^（n）与F_r^（n－1）比较接近或b₁值在两次迭代中比较接近时，即可得到F_r的值。

成对安装两个同一型号的角接触轴承，可按双列轴承进行寿命计算，其额定动载荷和当量动载荷均应取双列轴承的数值。如单列轴承的额定动载荷为C_r1，则双列轴承的额定动载荷为

角接触球轴承 C_r＝1.62C_r1

圆锥滚子轴承 C_r＝1.71Cr1