在静载荷作用下,零件将因受到拉、压、弯曲、扭转等作用而产生变形,产生拉应力、压应力、弯曲应力、切应力、扭应力等。
拉、压应力的强度计算公式为
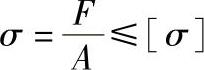
式中 F——零件受拉(或受压)的力(N);
A——零件截面积(mm2);
σ——拉(或压)应力(MPa);
[σ]——零件材料许用拉(压)应力(MPa)。
弯曲应力计算式为
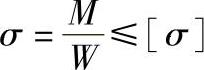
式中 M——零件受弯力矩(N·mm);
W——零件抗弯截面系数(mm3);
σ——弯曲应力(MPa);
[σ]——许用弯曲应力(MPa)。
扭应力计算式为
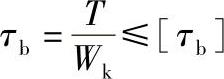
式中 T——零件所受转矩(N·mm);
Wk——零件的抗扭截面系数(mm3);
τb——扭应力(MPa);
[τb]——许用扭应力(MPa)。
由上述公式可见,提高静强度的途径有:
1)加大零件的截面积A(拉、压)、加大零件抗弯截面系数W(弯曲)、加大零件抗扭截面系数Wk。
2)减小拉(压)力F、减少受弯力矩M和转矩T。
3)增大许用应力[σ]或[τ],即选用高强度材料。
在材料、受力相同时,即[σ]或[τ]不变、F、M、T相同(不变)时,只有增大A、W、Wk,才能提高其强度。
各种截面形状的抗弯、抗扭截面系数,在截面积相同(即不增加材料用量和尺寸)时,形状不同,其抗弯、抗扭截面系数差别很大。表2.2-2列出了截面积相同而截面形状不同时抗弯截面系数的比较,以及抗弯截面系数相同而形状不同时,其材料截面积(重量)的比较。由此表可看出:截面积(重量)相同时,立式长方形件的抗弯截面系数(抗弯强度)为正方形件的2倍以上,工字形件的抗弯截面系数是正方形件的5.5倍。而当截面系数(抗弯强度)相同时,立式长方形件的截面积(材料重量)约为正方形件的一半,工字形件的截面积(材料重量)只有正方形件的1/5~1/8。可见构件的形状对抗弯强度有极大影响。
表2.2-2 不同截面形状对抗弯强度及材料用量的影响
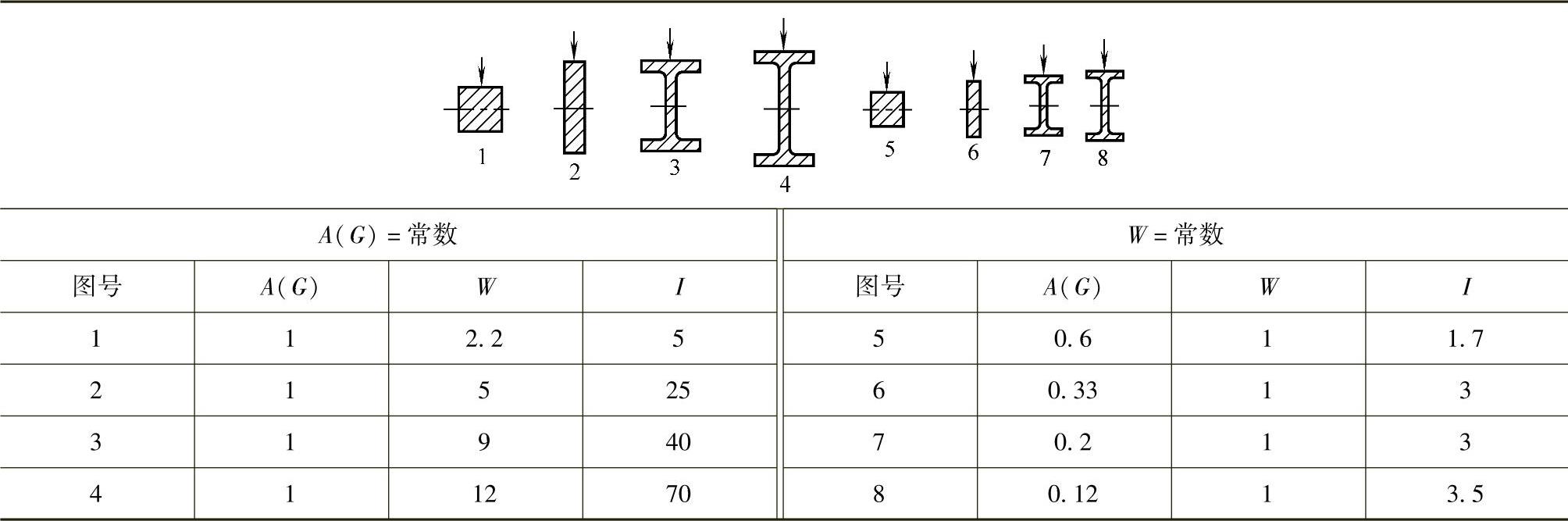
注:1.G为截面内材料面积重量比,假设材料相同。
2.I为构件的截面惯性矩相对值。
表2.2-3为各种不同形状构件(或型材)的截面积、截面惯性矩及截面抗弯系数的计算式,可作为构件形状设计或选择型材时,不同抗弯强度及承受动态力时抗弯惯性矩的比较。
在表2.2-3中,序号1的空心轴截面计算式,当管子内径d=0时便成为实心轴截面计算式。轴截面的抗弯截面系数W及惯性矩I,可以用来衡量轴的抗弯及受力变形的能力。表2.2-4列出了截面积A相同的情况下,不同的空心轴内、外径比值变化时,相同截面积空心轴的W、I值均比实心轴大,而且空心轴的内、外径比值越大,其W、I值比实心轴高出越多。这说明空心轴的强度和刚度比实心轴要高,也说明形状变化对零件强度有很大影响。
表2.2-3 常用构件截面形状的惯性矩I及抗弯截面系数W
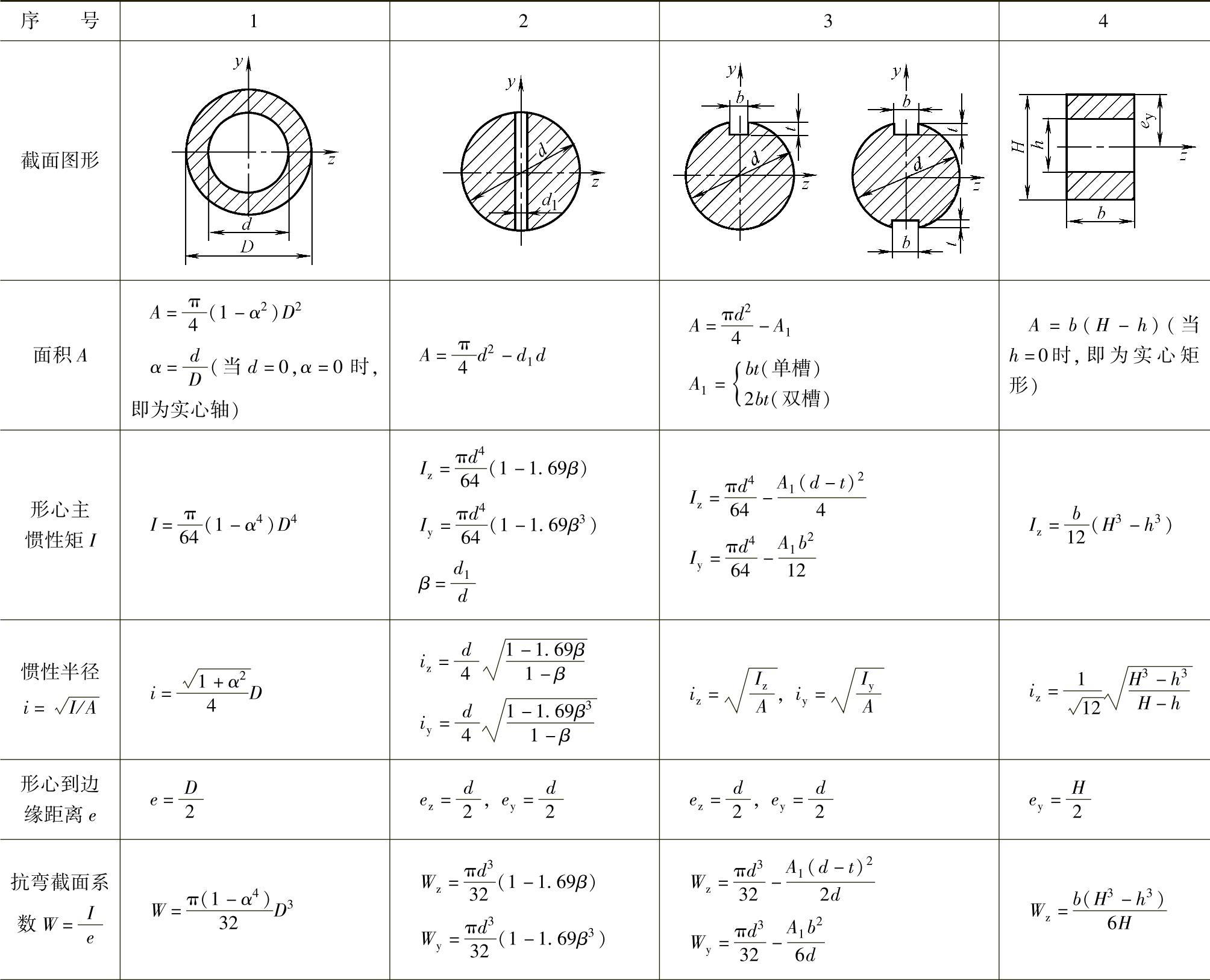
(续)(https://www.xing528.com)
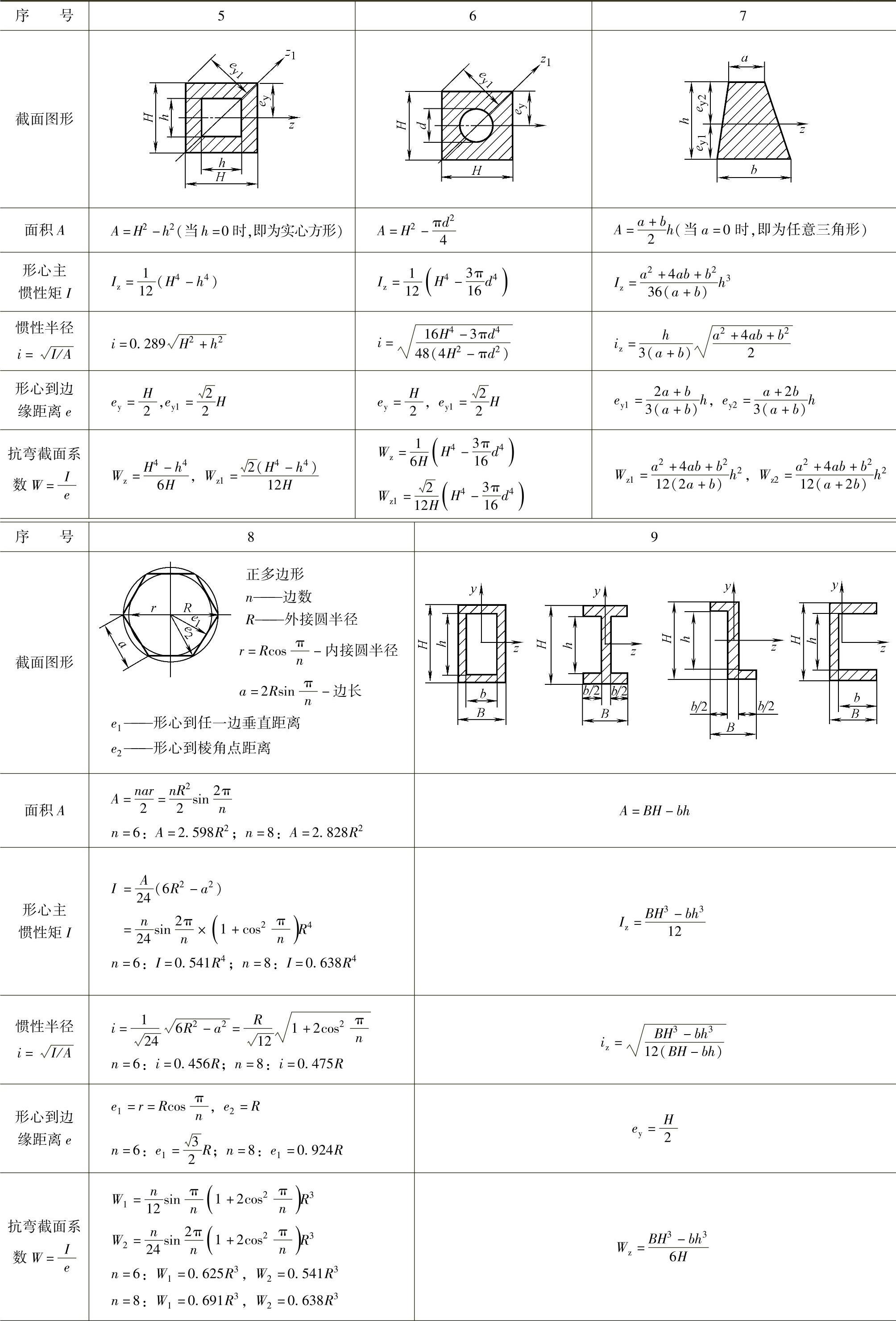
(续)
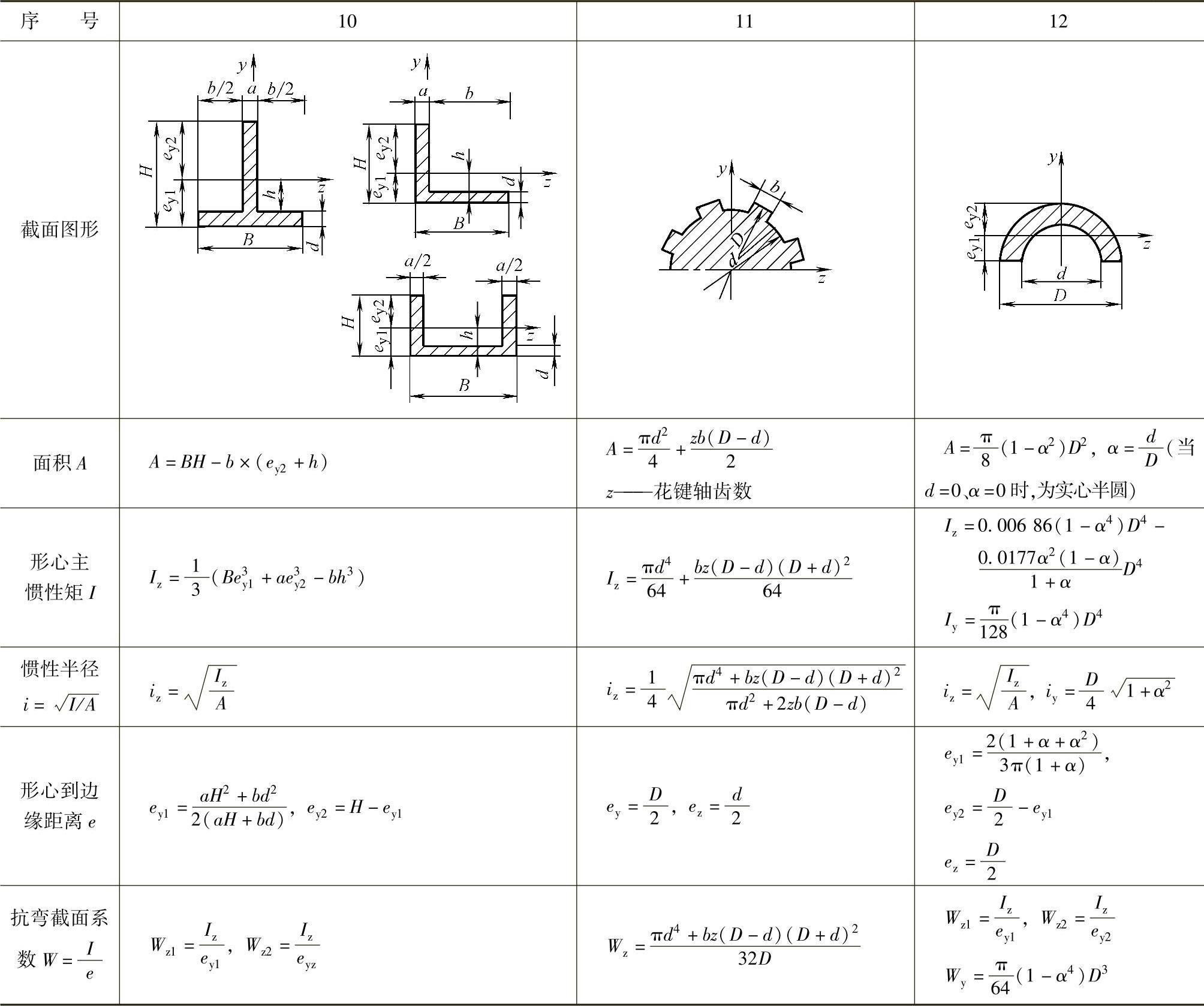
表2.2-4 空心轴与实心轴抗弯强度及刚度比较

注:D0—空心轴内径;D—空心轴外径;W0—空心轴抗弯截面系数;W—实心轴抗弯截面系数;I0—空心轴截面惯性矩;I—实心轴截面惯性矩。
对于悬臂梁结构件,在可能缩短悬臂长度时,应尽量减少长度,以减少悬臂根部所受的弯曲力矩,即减小根部弯曲应力,如图2.2-1所示。如不能缩短悬臂长度,应设法
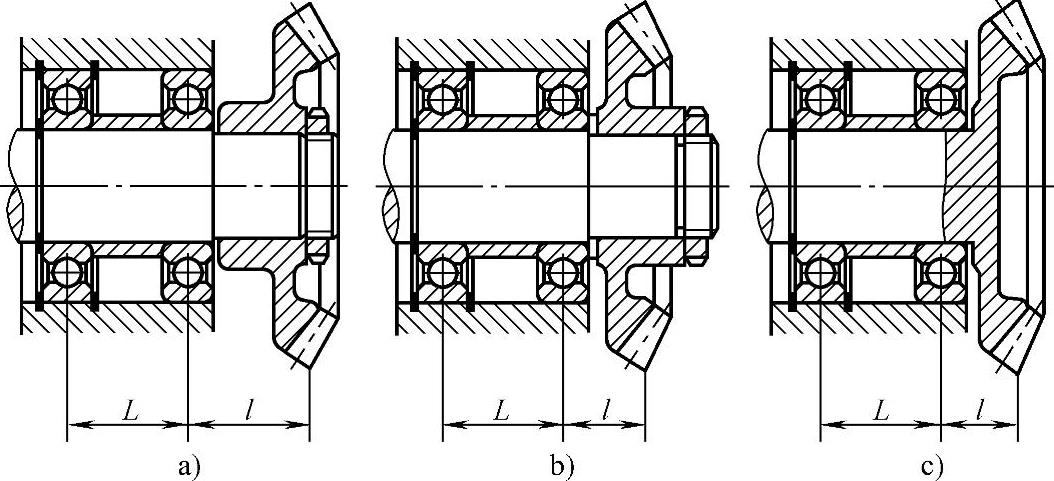
图2.2-1 减小伸出长度的结构
a)L/l≈1 b)L/l≈1.6 c)L/l≈2.1
加大悬臂根部的截面积或抗弯截面系数(如在梁的纵向加上斜肋),如图2.2-2所示。

图2.2-2 增加根部的面积或抗弯截面系数
由于材料的抗拉和抗压强度比抗弯强度大得多,故一些零件如能改变形状结构,使其抗弯结构变为抗拉、抗压结构,将使受力强度大增。如图2.2-3所示,板状结构形状改为两侧受力的三角斜向结构,则构件由受力弯曲变为受拉、压,强度大增,变形很小。如图2.2-4所示,悬臂薄壁圆柱筒若改为圆锥形筒,则锥筒不仅受到弯曲,而且上半部受拉力,下半部受压力,力F的一部分成为拉、压分力,减少了弯曲力,从而减少了弯曲变形。
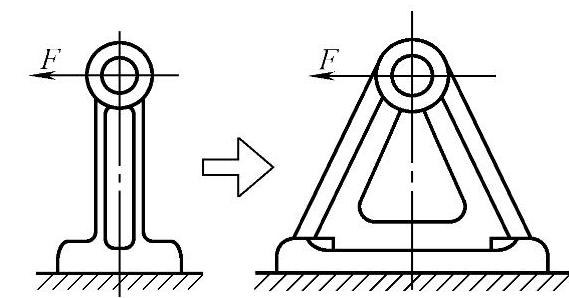
图2.2-3 支承座
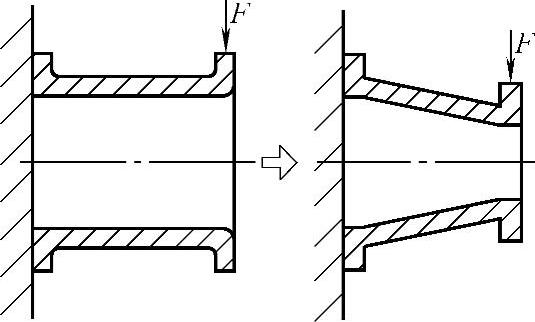
图2.2-4 悬臂薄壁筒
应力集中是降低零件疲劳强度的主要原因之一。断面变化剧烈处的应力集中十分严重,因而台阶轴、台阶面的交界处,必须尽量采用大圆角、锥角、斜面过渡。
图2.2-5所示是台阶轴交界处采用不同圆角半径过渡时与弯曲和扭转有效应力集中系数Kσ和Kτ的关系曲线。图中,过渡圆角半径r越小,应力集中系数Kσ、Kτ越大,疲劳强度越低。σb为不同抗拉强度材料的曲线,虚线ασ、ατ分别为理论弯曲应力集中系数和理论扭转应力集中系数的变化曲线。
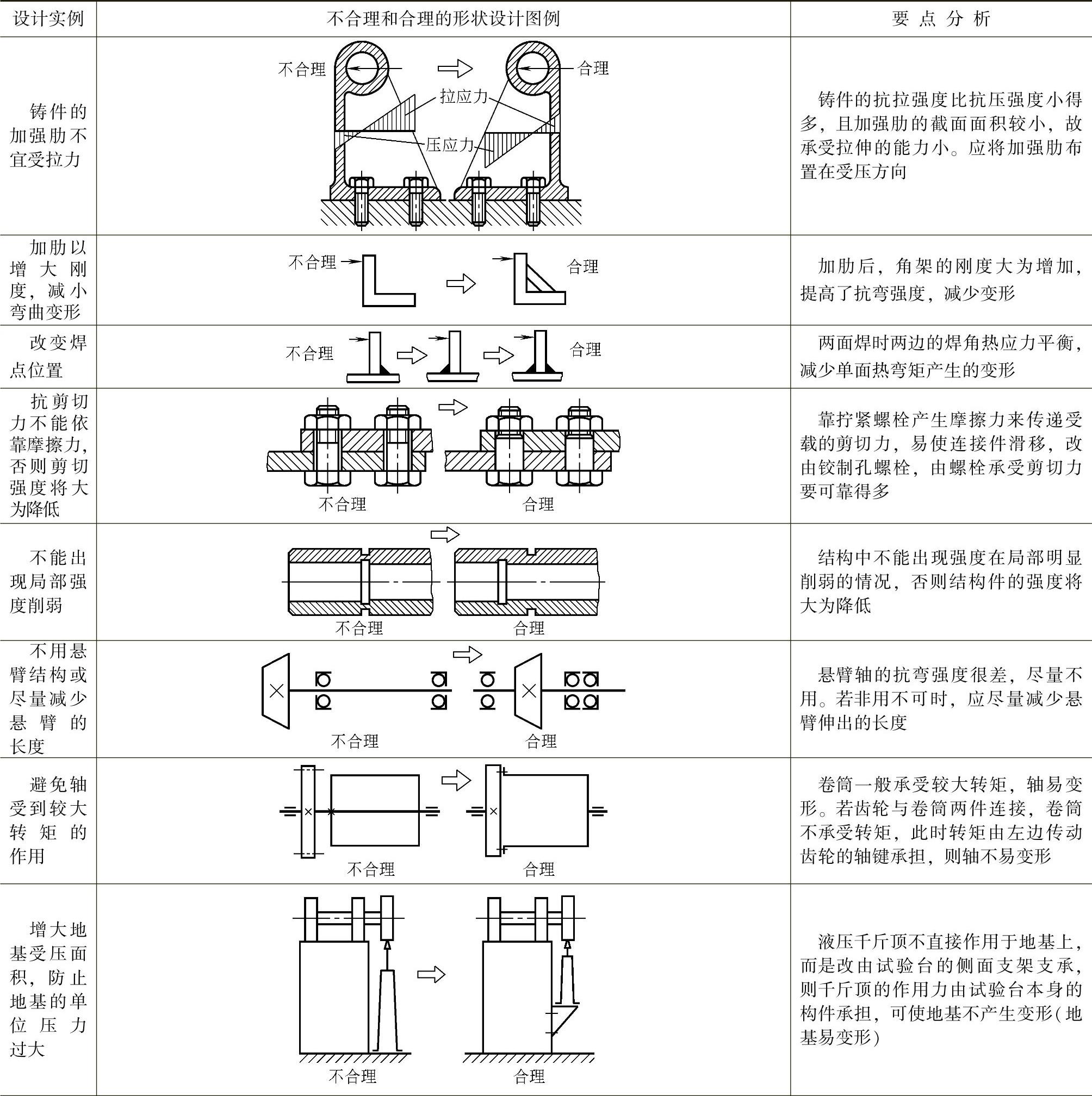
表2.2-5为考虑零件强度的形状设计实例。
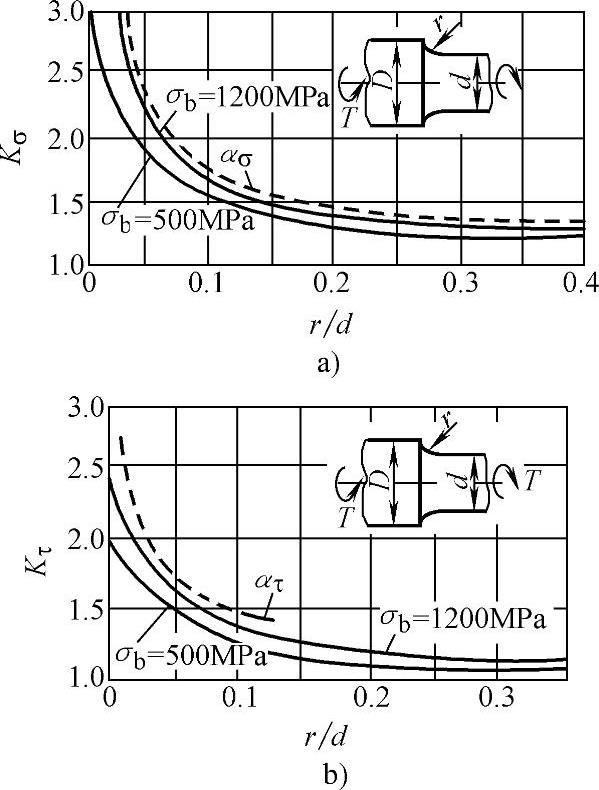
图2.2-5 (D/d=2)时有效应力集中系数
a)弯曲 b)扭转
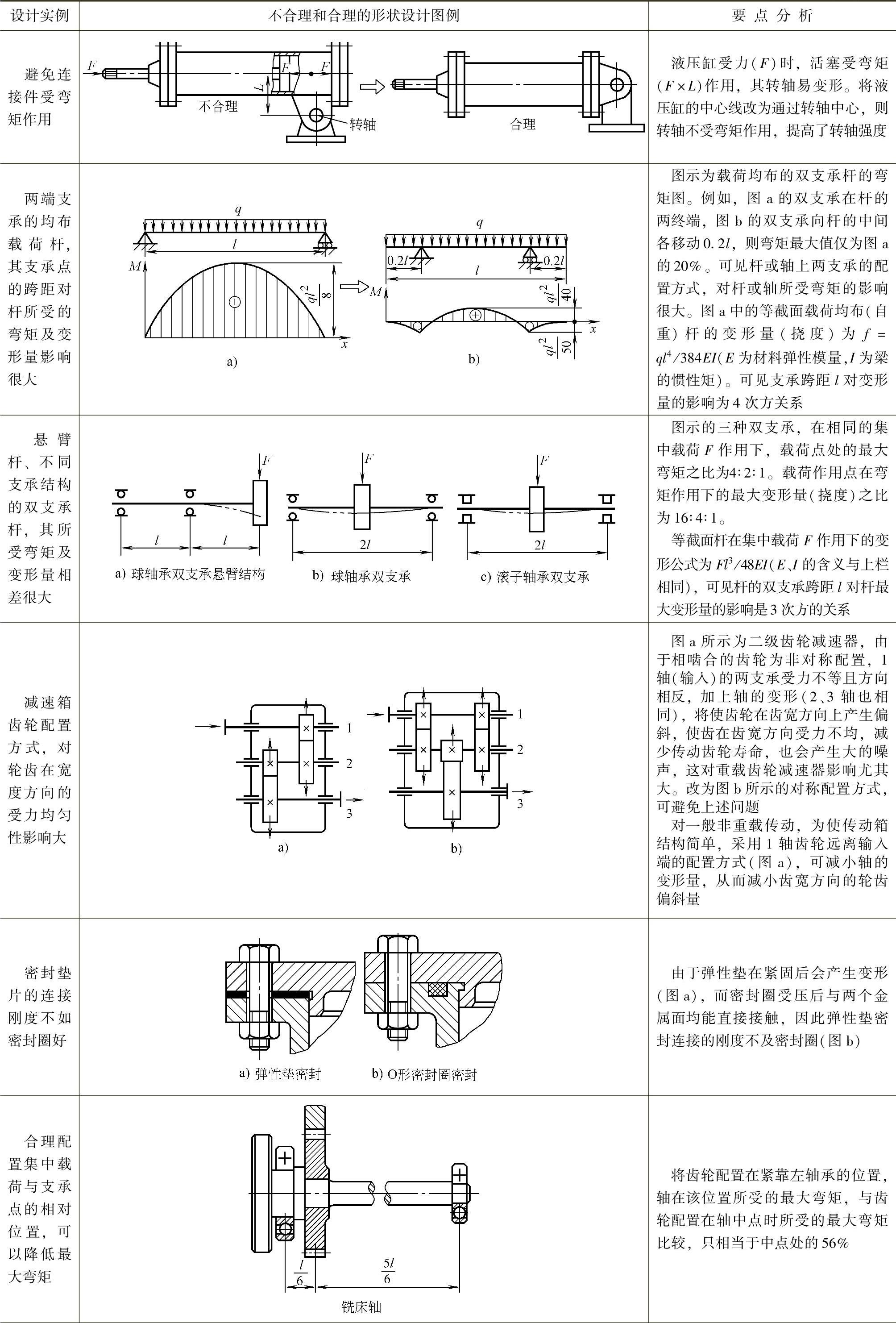
表2.2-5 考虑零件强度的形状设计实例
(续)
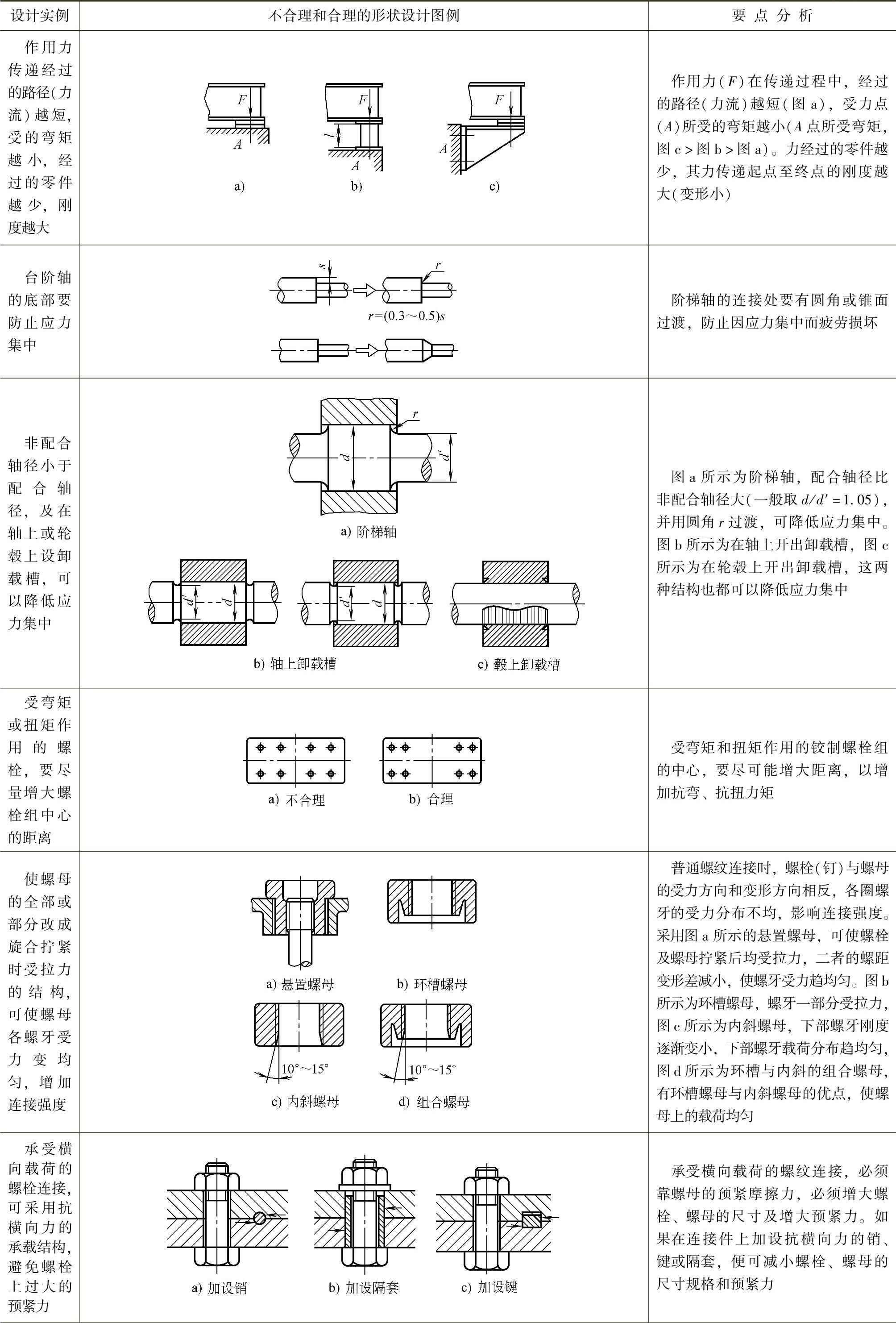
(续)
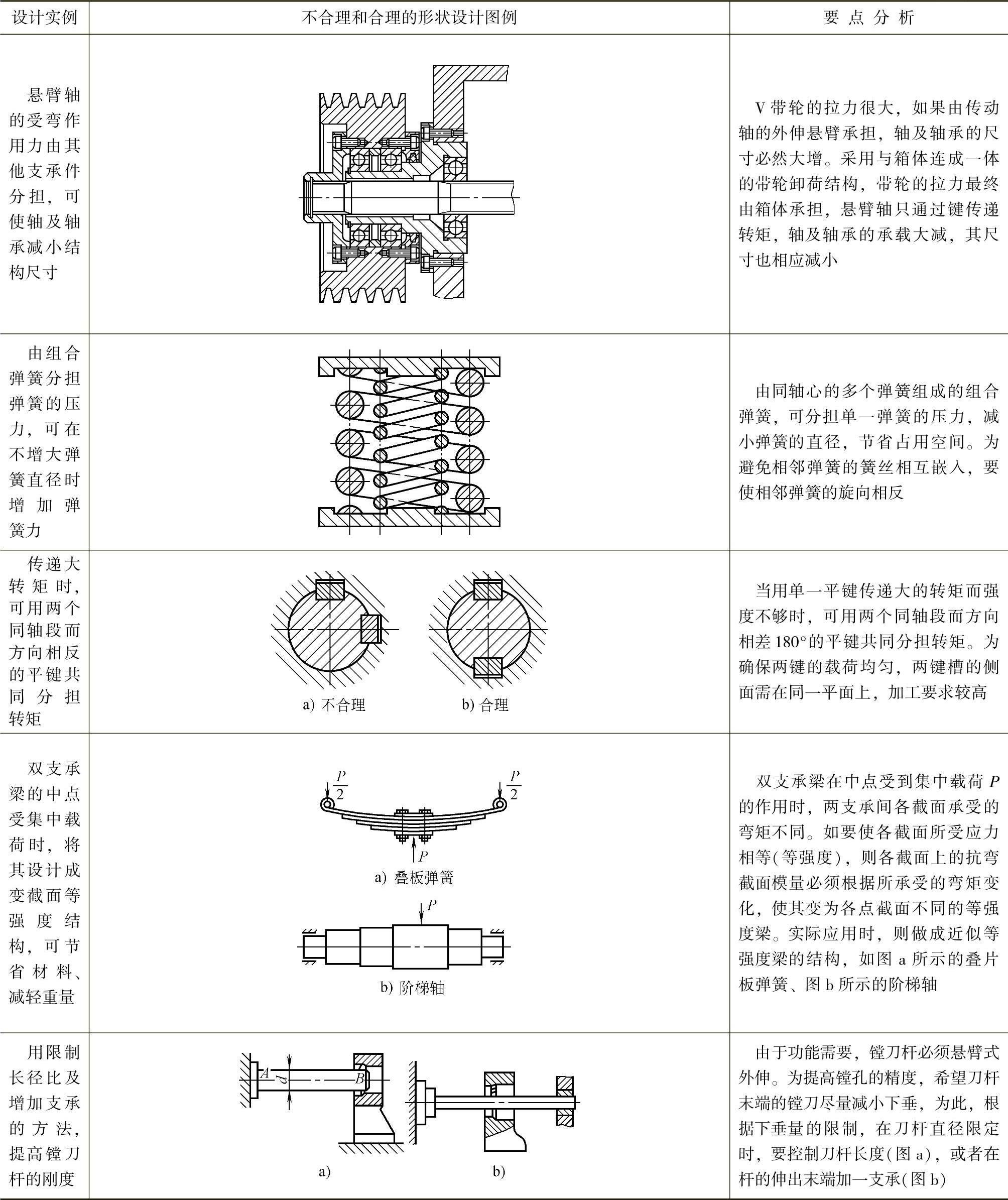
(续)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




