超声波换能器背衬的设计优化

为实现宽带脉冲超声波纳米颗粒检测，除了限制激励脉冲的宽度和采用低Qm值的压电晶片，还需对探头背衬以及晶片前部的阻抗匹配层加以优化设计。

首先对于探头背衬而言，如果背衬的声阻抗与压电晶片的声阻抗相同，并且具备尽可能大的声衰减系数，那么压电晶片产生的后向超声波就可以最有效地进入背衬，然后被吸收，最终得到的将是理想的检测波形。

目前，超声波探头的背衬多采用钨粉加环氧树脂制成的复合材料，此外还有金属-金属、金属-高分子材料背衬等。依赖于控制基质内固体颗粒大小以及数量，可以实现探头背衬声阻抗以及衰减系数的调节。背衬中产生声衰减的因素主要为两个：其一是基质内固体颗粒所产生的散射衰减，超声波进入背衬经过复杂无序的散射后，转化为热能；其二是由于背衬材料的黏滞效应，导致背衬内质点间相互摩擦，使得声能转化为热能。

平面波在背衬中的声衰减以衰减系数α表示：

式中　P0——初始声压；

x——传播距离。

假设背衬中基质材料的密度为ρ1，拉梅常数为λ1和μ1；背衬中填料的颗粒直径为r0，密度为ρ2，拉梅常数为λ2和μ2；背衬复合材料的密度为ρ，拉梅常数为λ和μ。当频率为ω的平面纵波在背衬中传播时，其声传播特性与基质和填料的物性以及填料在背衬中所占的比例有关。参照Waterman和Truell，将背衬复合材料中的声传播常数做如下定义：

式中　vl——背衬复合材料的纵波声速；

α——声衰减系数。

背衬中的声传播常数β满足下列方程：

式中　n0——背衬中每单位体积内固体颗粒的个数；

k1——基质材料中的纵波波数；

k2——填充材料中的纵波波数；

f（0）——单个固体颗粒的前向散射振幅；

f（π）——单个固体颗粒的后向散射振幅；

Am——超声在背衬复合材料中的散射系数。

按照Ying和Truell有关超声在固体中的单散射理论，得到如下线性方程组：

式中　jm——m阶球贝塞尔函数；

hm——m阶球汉克尔函数。(www.xing528.com)

此外

求解上述线性方程组，可得到超声波在背衬复合材料中传播时，遇到弹性填充颗粒后在颗粒外部的散射系数Am。

以环氧树脂中添加钨粉作为算例，分析复合材料中的声衰减系数随k1r0的变换规律，取r0=100μm，数值计算中所需的力学性能见表5.2。

表5.2　钨粉、环氧树脂的力学性能参数

图5.4　背衬复合材料声衰减系数随k1r0变化曲线

从图5.4中可以看出，背衬复合材料中的声衰减随钨粉体积浓度的增加显著增大，但其衰减系数极大值基本都处于k1r0≈0.4附近，意味着如果已知压电晶片的中心频率，通过控制钨粉颗粒的尺寸可以实现背衬复合材料的最大衰减。

此外，为实现与压电晶片声阻抗的匹配，还需要对背衬复合材料的声阻抗做理论上的计算分析，寻找其声阻抗与钨粉体积浓度之间的关系。参照Sayer的自相关理论，首先确定背衬复合材料的等效密度、等效弹性常数，然后求出复合材料的声速与声阻抗：

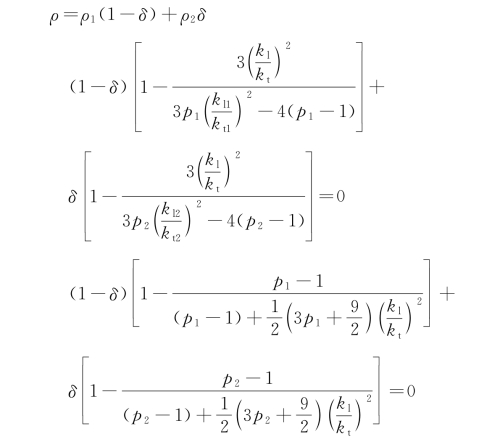
其中

式中　kl1、kl2——背衬复合材料中基质材料与填充材料的纵波波数；

kt1、kt2——基质材料与填充材料的横波波数；

kl、kt——背衬复合材料中的等效纵波数与等效横波数；

δ——背衬复合材料中钨粉的体积浓度。

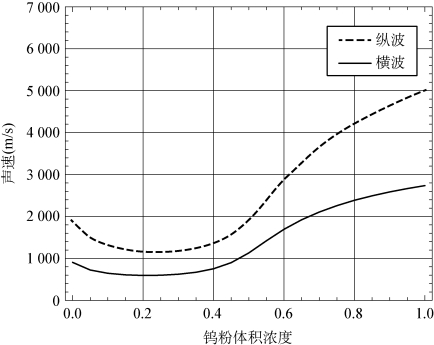
图5.5　钨粉/环氧树脂复合材料纵波、横波声速随钨粉体积浓度变化曲线

图5.6　钨粉/环氧树脂复合材料纵波、横波声阻抗随钨粉体积浓度变化曲线

从图5.5中可以看出，当背衬复合材料中钨粉体积浓度较低时，随钨粉体积浓度的增加，超声波声速下降，这主要是由于复合材料中填充材料颗粒散射的原因，主要在超声波频率较低时出现。当钨粉体积浓度超过50%时，声速随钨粉体积浓度的增加快速升高，逐渐接近于纯钨中的声速。

从图5.6中可以发现，当背衬复合材料中钨粉体积浓度低于40%时，声阻抗随钨粉体积浓度的改变不甚明显，钨粉体积浓度在40%～60%变化区间内，声阻抗会发生急剧变化，因此在该区间内对钨粉比例的控制要求较高。