如何设计系数矩阵进行颗粒系反演计算？

无论何种理论模型，最终的目的都是要得到颗粒相的粒度分布，其原理是采用理论模型预测出依赖于超声频率和粒径的声衰减谱，并将其与实际测得的超声衰减谱比较，显然这种差距越小，表明待检颗粒两相介质与理论模型的预测越接近。以下为Phillips-Twomey-NNLS反演算法的具体过程。

考虑多分散颗粒系的声衰减方程：

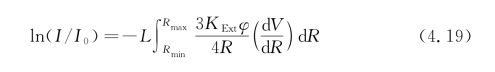
式中　L——声程长度；

dV/dR——颗粒分布的体积频度分布表达式，是颗粒半径R的函数。

上式为第一类Fredholm积分方程，目前尚没有理论解，按通常做法可以用数值积分等式将右边离散：

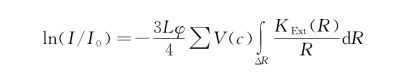
考虑多个频率情况，可得到一个矩阵形式如下：

式中　A——系数矩阵，其中的每个元素是由对式（4.19）右边∆R区间内的核函数积分求得；

F——离散化的颗粒尺寸频度分布；

G——不同频率下声衰减构成的向量，由实际测量得到。

通常对式（4.20）的矩阵直接求解是非常困难的，将非负最小二乘法引入其中，让线性方程组满足下面的条件：

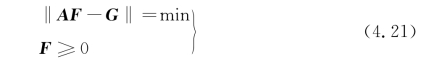
式中，F≥0表示对其所有分量有Fi≥0，i=1，2，…，n，这里的n为分档数。

实际上，按照上式解出的结果，受到向量G的误差影响仍然较大，这种误差在测量过程中是难以避免的，所以常得不到理想的解，为此需要引入光滑因子γ和光顺矩阵H，其中H定义为

(www.xing528.com)

于是式（4.20）可改写为

利用最小非负二乘法对上式求解：

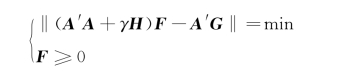
式中　A'——系数矩阵的转置；

γ——光滑因子。

事实上，光滑因子γ对方程的解影响很大。γ=0，式（4.22）退化为一般的求逆阵算法，由此得到的解呈剧烈振荡形。逐渐增大γ后，解的振荡减少，逐渐变得光顺，一般分布会变宽。γ值过大，则会过于光顺，仍会造成误差。

本研究采用基于GCV技术（generalized cross validation technique），经过一些推导后，问题归结为对下面的γ的函数求最小值而得到对应的γ值：

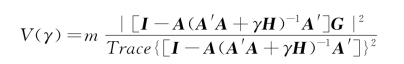
式中　I——单位矩阵；

M——所用频率数，也是单位矩阵的阶数；

||——求范数；

Trace——求矩阵的迹。

系数矩阵的设计同样重要，一方面要保证在选取的颗粒系区间中要有足够多的计算点，尤其是对小的颗粒，避免由于计算点间隔过大产生误差；另一方面，计算点取得过多过密，会使计算量增大。实际应用中，系数矩阵的设计应根据所测量颗粒系的范围宽度、分布情况以及所要求的测量精度等来确定。

图4.14为专门针对超声衰减谱测粒反演计算而编写的分析程序。

图4.14　反演计算程序